Question 6:
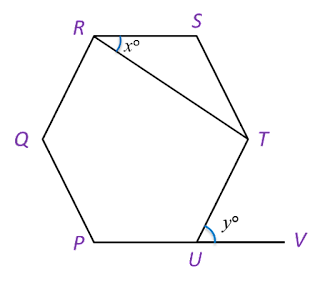
In diagram below, PQRSTU is a regular hexagon QUV is a straight line.
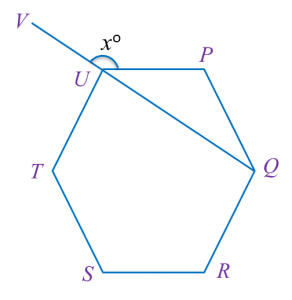
Find the value of x.
Solution:
Each interior angle=(6−2)×180o6=120o∠PUQ=180o−120o2=30o (△PUQ is a isosceles triangle)xo=180o−30o=150ox=150
In diagram below, PQRSTU is a regular hexagon QUV is a straight line.

Find the value of x.
Solution:
Each interior angle=(6−2)×180o6=120o∠PUQ=180o−120o2=30o (△PUQ is a isosceles triangle)xo=180o−30o=150ox=150
Question 7:
In diagram below, PQRSTU is a hexagon. UPE, PQF, QRG, RSH and UTJ are straight lines.
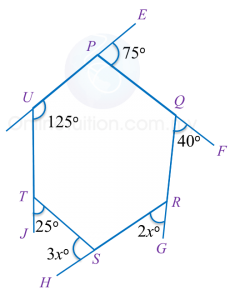
Find the value of x.
Solution:
Sum of all the exterior angles of any polygon=360o25o+3xo+2xo+40o+75o+55o=360o5xo+195o=360o 5xo=360o−195o =165oxo=165o÷5 =33o x=33
In diagram below, PQRSTU is a hexagon. UPE, PQF, QRG, RSH and UTJ are straight lines.

Find the value of x.
Solution:
Sum of all the exterior angles of any polygon=360o25o+3xo+2xo+40o+75o+55o=360o5xo+195o=360o 5xo=360o−195o =165oxo=165o÷5 =33o x=33
Question 8:
In Diagram below, A, B, C, D and E are vertices of a 9 sided regular polygon.
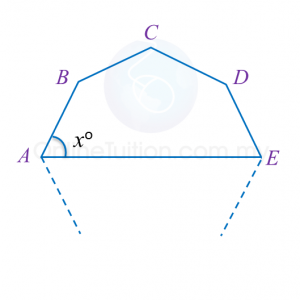
Find the value of x.
Solution:
Exterior angle =360o9=40oInterior angle=180o−40o=140oSum of interior angles of pentagon ABCDE=(5−2)×180o=540oxo+140o+140o+140o+xo=540o2xo=540o−420o =120o xo=60o x=60
In Diagram below, A, B, C, D and E are vertices of a 9 sided regular polygon.

Find the value of x.
Solution:
Exterior angle =360o9=40oInterior angle=180o−40o=140oSum of interior angles of pentagon ABCDE=(5−2)×180o=540oxo+140o+140o+140o+xo=540o2xo=540o−420o =120o xo=60o x=60