1.2.1 Angles and Lines II, PT3 Practice

1.2.1 Angles and Lines II, PT3 Practice

Question 1:

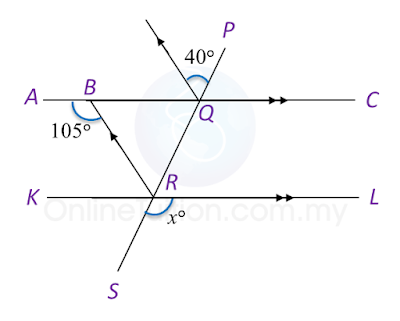
In Diagram below, PQRS, ABQC and KRL are straight lines.

Find the value of x.

Solution:

\begin{array}{l} ∠ K R B + ∠ A B R = 180^{o} \leftarrow Sum of interior angles \\ ∠ K R B + 105^{o} = 180^{o} \\ ∠ K R B = 180^{o} - 105^{o} \\ ∠ K R B = 75^{o} \\ ∠ B R Q = 40^{o} \leftarrow Corresponding angle \\ x^{o} = ∠ S R L = ∠ K R Q \leftarrow \begin{array}{l} Vertically \\ opposite angle \end{array} \\ x^{o} = 75^{o} + 40^{o} \\ = 115^{o} \\ x = 115 \end{array}

Question 2:

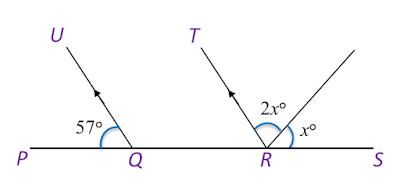
(a) In Diagram below, PQR and SQT are straight lines.

Find the value of x.

(b) In Diagram below, PQRS is a straight line. Find the value of x.

Solution:

(a)

\begin{array}{l} ∠ P Q T = ∠ R Q S \\ x^{o} + 90^{o} = 155^{o} \\ x^{o} = 155^{o} - 90^{o} \\ = 65^{o} \\ x = 65 \end{array}

(b)

\begin{array}{l} ∠ Q R T = 57^{o} \\ x^{o} + 2 x^{o} = 180^{o} - 57^{o} \\ 3 x^{o} = 123^{o} \\ x^{o} = \frac{123^{o}}{3} \\ x^{o} = 41^{o} \\ x = 41 \end{array}

Question 3:

In Diagram below, PQR is a straight line. Find the value of x.

Solution:

\begin{array}{l} x^{o} = ∠ Q R T + ∠ T R S \\ ∠ Q R T = 40^{o} \\ ∠ T R S = 180^{o} - 135^{o} \\ = 45^{o} \\ Hence, x^{o} = 40^{o} + 45^{o} \\ x^{o} = 85^{o} \\ x = 85 \end{array}

Question 4:

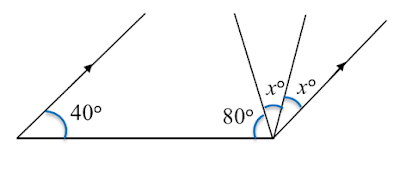
In Diagram below, find the value of x.

Solution:

40^o + 80^o + x^o+ x^o = 180^o

2x^o = 180^o – 120^o

2x^o = 60^o

x^o= 30^o

x = 30

Question 5:

In Diagram below, PQR is an isosceles triangle and QRS is a straight line.

Find the values of x and y.

Solution:

\begin{array}{l} ∠ P R Q = 180^{o} - 110^{o} = 70^{o} \\ ∠ P R Q = ∠ P Q R = 70^{o} \\ y^{o} = 180^{o} - 70^{o} - 70^{o} \\ = 40^{o} \\ y = 40 \\ x^{o} = 110^{o} - 40^{o} \\ = 70^{o} \\ x = 70 \end{array}