9.4 First Derivatives of the Quotient of Two Polynomials

Posted on April 22, 2020 by user

9.4 Find the Derivatives of a Quotient using Quotient Rule

Method 1

The Quotient Rule

Example:

Method 2 (Differentiate Directly)

Example:

Given that y = \frac{x^{2}}{2 x + 1}, find \frac{d y}{d x}

Solution:

\begin{array}{l} y = \frac{x^{2}}{2 x + 1} \\ \frac{d y}{d x} = \frac{(2 x + 1) (2 x) - x^{2} (2)}{{(2 x + 1)}^{2}} \\ = \frac{4 x^{2} + 2 x - 2 x^{2}}{{(2 x + 1)}^{2}} = \frac{2 x^{2} + 2 x}{{(2 x + 1)}^{2}} \end{array}

Practice 1:

Given that y = \frac{4 x^{3}}{{(5 x + 1)}^{3}}, find \frac{d y}{d x}

Solution:

\begin{array}{l} y = \frac{4 x^{3}}{{(5 x + 1)}^{3}} \\ \frac{d y}{d x} = \frac{{(5 x + 1)}^{3} (12 x^{2}) - 4 x^{3} .3 {(5 x + 1)}^{2} .5}{{[{(5 x + 1)}^{3}]}^{2}} \\ = \frac{{(5 x + 1)}^{3} (12 x^{2}) - 60 x^{3} {(5 x + 1)}^{2}}{{(5 x + 1)}^{6}} \\ = \frac{(12 x^{2}) {(5 x + 1)}^{2} [(5 x + 1) - 5 x]}{{(5 x + 1)}^{6}} \\ = \frac{(12 x^{2}) {(5 x + 1)}^{2} (1)}{{(5 x + 1)}^{6}} \\ = \frac{12 x^{2}}{{(5 x + 1)}^{4}} \end{array}

9.2 First Derivative for Polynomial Function

Posted on April 22, 2020 by user

9.2 First Derivative for Polynomial Function

(A) Differentiating a Constant

(B) Differentiating Variable with Index n

(C) Differentiating a Linear Function

(D) Differentiating a Polynomial Function

(E) Differentiating Fractional Function

(F) Differentiating Square Root Function

Long Questions (Question 4)

Posted on April 21, 2020 by user

Question 4:

In the diagram above, AXB is an arc of a circle centre O and radius 10 cm with ∠AOB = 0.82 radian. AYB is an arc of a circle centre P and radius 5 cm with ∠APB = θ. Calculate:

the length of the chord AB,
the value of θ in radians,
the difference in length between the arcs AYB and AXB.

Solution:

(a)
$\begin{array}{l} \frac{1}{2} A B = \sin 0.41 \times 10 \to (Change the calculator to Rad mode) \\ \frac{1}{2} A B = 3.99 \\ ∴ The length of chord A B = 3.99 \times 2 = 7.98 c m . \end{array}$

(b)
$\begin{array}{l} Let \frac{1}{2} θ = α, θ = 2 α \\ \sin α = \frac{3.99}{5} \\ α = 0.924 rad \\ ∴ θ = 0.924 \times 2 = 1.848 radian . \end{array}$

(c)
Using s = rθ
Arcs AXB = 10 × 0.82 = 8.2 cm
Arcs AYB = 5 × 1.848 = 9.24 cm

Difference in length between the arcs AYB and AXB
= 9.24 – 8.2
= 1.04 cm

Long Questions (Question 3)

Posted on April 21, 2020 by user

Question 3:
Diagram below shows a sector QPR with centre P and sector POQ, with centre O.

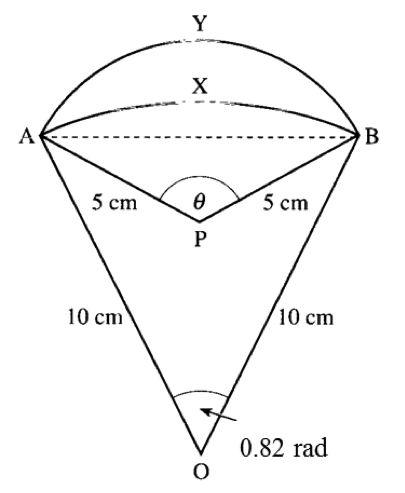
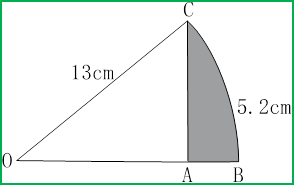
It is given that OP = 17 cm and PQ = 8.8 cm.
[Use π = 3.142]
Calculate
(a) angle OPQ, in radians,
(b) the perimeter, in cm, of sector QPR,
(c) the area, in cm², of the shaded region.

Solution:

\begin{array}{l} (a) \\ ∠ O P Q = ∠ O Q P \\ x + x + 30 = 180 \\ 2 x = 150 \\ x = 75 \\ ∠ O P Q = \frac{75 \times 3.142}{180} \\ = 1.3092 radians \end{array}

\begin{array}{l} (b) \\ Length of arc Q R = r θ \\ = 8.8 \times 1.3092 \\ = 11.52 cm \\ Perimeter of sector Q P R \\ = 11.52 + 8.8 + 8.8 \\ = 29.12 cm \end{array}

\begin{array}{l} (c) \\ 30^{o} = \frac{30 \times 3.142}{180} = 0.5237 rad \\ Area of segment P Q \\ = \frac{1}{2} r^{2} (θ - \sin θ) \\ = \frac{1}{2} \times 17^{2} \times (0.5237 - \sin 30) \\ = \frac{1}{2} \times 289 \times (0.5237 - 0.5) \\ = 3.4247 {cm}^{2} \\ Area of sector Q P R \\ = \frac{1}{2} r^{2} θ \\ = \frac{1}{2} \times {8.8}^{2} \times 1.3092 \\ = 50.692 {cm}^{2} \\ Area of shaded region \\ = 3.4247 + 50.692 \\ = 54.1167 {cm}^{2} \end{array}

Long Questions (Question 2)

Posted on April 21, 2020 by user

Question 2:
Diagram below shows a semicircle PTQ, with centre O and quadrant of a circle RST, with centre R.

[Use π = 3.142]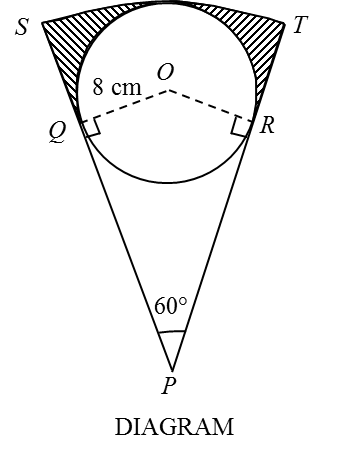
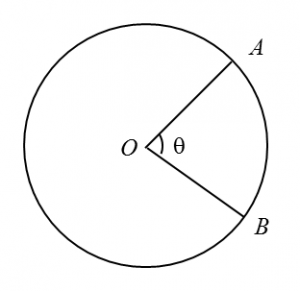
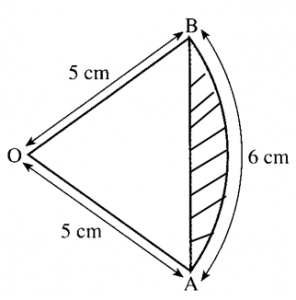
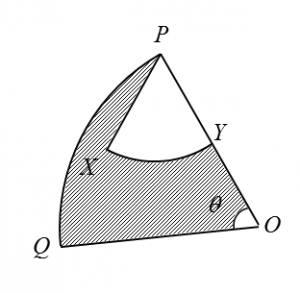Calculate
(a) the value of θ, in radians,
(b) the perimeter, in cm, of the whole diagram,
(c) the area, in cm², of the shaded region.

Solution:

\begin{array}{l} (a) \\ \sin ∠ R O T = \frac{2.5}{5} \\ ∠ R O T = 30^{o} \\ θ = 180^{o} - 30^{o} = 150^{o} \\ = 150 \times \frac{π}{180} \\ = 2.618 rad \end{array}

\begin{array}{l} (b) \\ Length of arc P T = r θ \\ = 5 \times 2.618 \\ = 13.09 cm \\ Length of arc S T = \frac{π}{2} \times 2.5 \\ = 3.9275 cm \\ O R^{2} + {2.5}^{2} = 5^{2} \\ O R^{2} = 5^{2} - {2.5}^{2} \\ O R = 4.330 \\ Perimeter = 13.09 + 3.9275 + 2.5 + 4.330 + 5 \\ = 28.8475 cm \end{array}

\begin{array}{l} (c) \\ Area of shaded region \\ = Area of quadrant R S T - Area of quadrant R Q T \\ Area of quadrant R Q T \\ = Area of O Q T - Area of O T R \\ = \frac{1}{2} {(5)}^{2} \times (30 \times \frac{π}{180}) - \frac{1}{2} (4.33) (2.5) \\ = 1.1333 {cm}^{2} \\ Area of shaded region \\ = Area of quadrant R S T - Area of quadrant R Q T \\ = \frac{1}{2} {(2.5)}^{2} \times (90 \times \frac{π}{180}) - 1.1333 \\ = 3.7661 {cm}^{2} \end{array}

Long Questions (Question 1)

Posted on April 21, 2020 by user

Question 1:

Diagram shows a circle, centre O and radius 8 cm inscribed in a sector SPT of a circle at centre P. The straight lines, SP and TP, are tangents to the circle at point Q and point R, respectively.

[Use p= 3.142]

Calculate

(a) the length, in cm, of the arc ST,

(b) the area, in cm², of the shaded region.

Solution:
(a)

\begin{array}{l} For triangle O P Q \\ \sin 30^{\circ} = \frac{8}{O P} \\ O P = \frac{8}{\sin 30^{\circ}} = 16 cm \\ Radius of sector S P T = 16 + 8 = 24 cm \\ ∠ S P T = 60 \times \frac{3.142}{180} = 1.047 radian \\ Length of arc S T = 24 \times 1.047 = 25.14 cm \end{array}

(b)

\begin{array}{l} For triangle O P Q : \\ \tan 30^{\circ} = \frac{8}{Q P} \\ P Q = \frac{8}{\tan 30^{\circ}} = 13.86 cm \\ ∠ Q O R = 2 (60^{\circ}) = 120^{\circ} \\ Reflex angle ∠ Q O R = 360^{\circ} - 120^{\circ} = 240^{\circ} \\ 240^{\circ} = \frac{3.142}{180^{\circ}} \times 240^{\circ} = 4.189 radian \\ Area of shaded region \\ = (\begin{array}{l} Area of \\ sector S P T \end{array}) - (\begin{array}{l} Area of major \\ sector O Q R \end{array}) - (\begin{array}{l} Area of triangle \\ O P Q and O P R \end{array}) \\ = \frac{1}{2} {(24)}^{2} (1.047) - \frac{1}{2} {(8)}^{2} (4.189) - 2 (\frac{1}{2} \times 8 \times 13.86) \\ = 301.54 - 134.05 - 110.88 \\ = 56.61 {cm}^{2} \end{array}

Short Questions (Question 3 & 4)

Posted on April 21, 2020 by user

Question 3:

Diagram below shows a circle with centre O.

The length of the minor arc is 16 cm and the angle of the major sector AOB is 290^o.

Using π = 3.142, find

(a) the value of θ, in radians. (Give your answer correct to four significant figures)

(b) the length, in cm, of the radius of the circle.

Solution:

(a)

Angle of the minor sector AOB

= 360^o– 290^o

= 70^o

= 70^o×

\frac{3.142}{180}

= 1.222 radians

(b)

Using s = rθ

r × 1.222 = 16

radius, r = 13.09 cm

Question 4:

Diagram below shows sector OPQ with centre O and sector PXY with centre P.
Given that OQ = 8 cm, PY = 3 cm , ∠ XPY = 1.2 radians and the length of arc PQ = 6cm ,

calculate

( a) the value of θ , in radian ,

( b) the area, in cm² , of the shaded region .

Solution:
(a) s = r θ

6 = 8 θ

θ = 0.75 rad

(b)

Area of the shaded region

= Area of sector OPQ – Area of sector PXY

= \frac{1}{2} {(8)}^{2} (0.75) - \frac{1}{2} {(3)}^{2} (1.2)

= 24 – 5.4

= 18.6 cm²

Short Questions (Question 1 & 2)

Posted on April 21, 2020 by user

Question 1:

The figure shows the sector OCB of radius 13 cm at the centre O. The length of the arc CB = 5.2 cm. Find

(a) the angle in radians,

(b) the perimeter of the shaded region.

Solution:
(a)

\begin{array}{l} s = r θ \\ 5.2 = 13 (∠ C O B) \\ ∠ C O B = 0.4 radian \end{array}

(b)

\begin{array}{l} \cos ∠ C O B = \frac{O A}{O C} \\ \cos 0.4 = \frac{O A}{13} (change calculator to Rad mode) \\ O A = 11.97 cm \\ ∴ A B = 13 - 11.97 = 1.03 cm \\ C A = \sqrt{13^{2} - {11.97}^{2}} \\ C A = 5.07 cm \end{array}

Perimeter of the shaded region = 5.07 + 1.03 + 5.2 = 11.3 cm.

Question 2:

The figure shows the sector AOB of a circle, centre O and radius 5 cm. The length of the arc AB is 6 cm. Find the area of:

(a) the sector AOB,

(b) the shaded region.

Solution:
(a) Arc AB = 6cm

s = r θ

6 = 5 θ

θ = 6/5 rad

\begin{array}{l} Area of sector A O B \\ = \frac{1}{2} r^{2} θ = \frac{1}{2} {(5)}^{2} (\frac{6}{5}) = 15 c m^{2} \end{array}

(b)

\begin{array}{l} Area of shaded region \\ = \frac{1}{2} r^{2} (θ - \sin θ) (change calculator to Rad mode) \\ = \frac{1}{2} {(5)}^{2} (\frac{6}{5} - \sin \frac{6}{5}) \\ = 3.35 {cm}^{2} \end{array}

8.3 Area of a Sector of a Circle

Posted on April 21, 2020 by user

8.3 Area of a Sector of a Circle
(A) Area of a Sector of a Circle

1. If a circle divided into two sectors of different sizes, the smaller sector is known as the minor sector while the larger sector is known as the major sector.