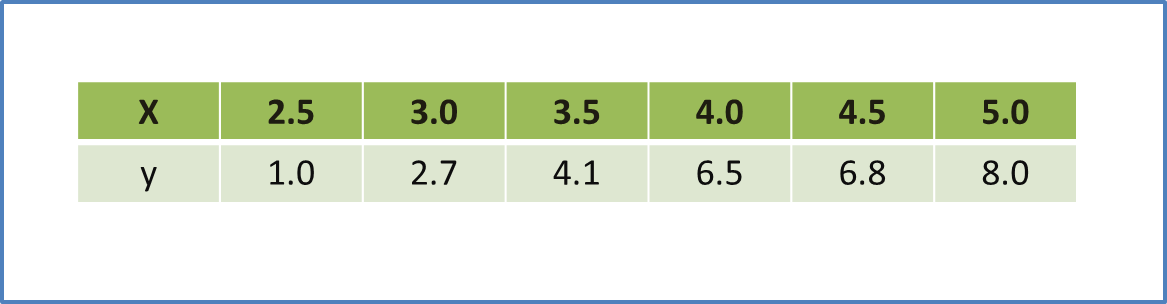
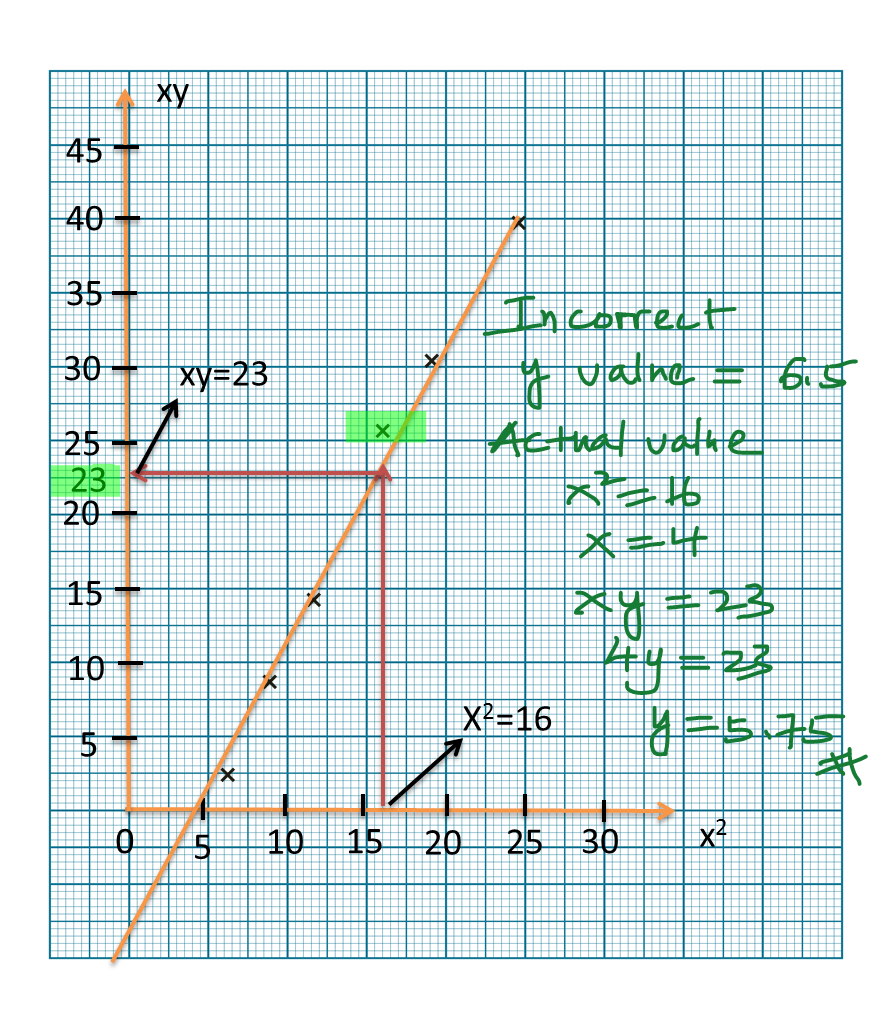
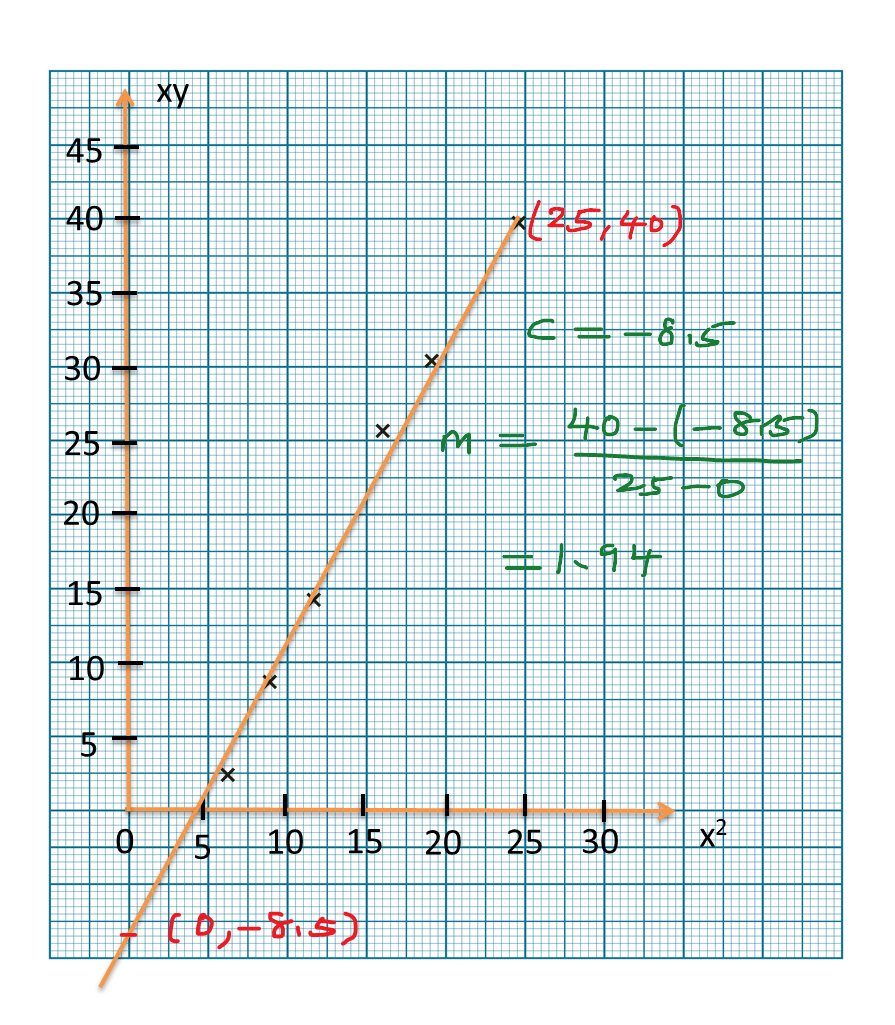
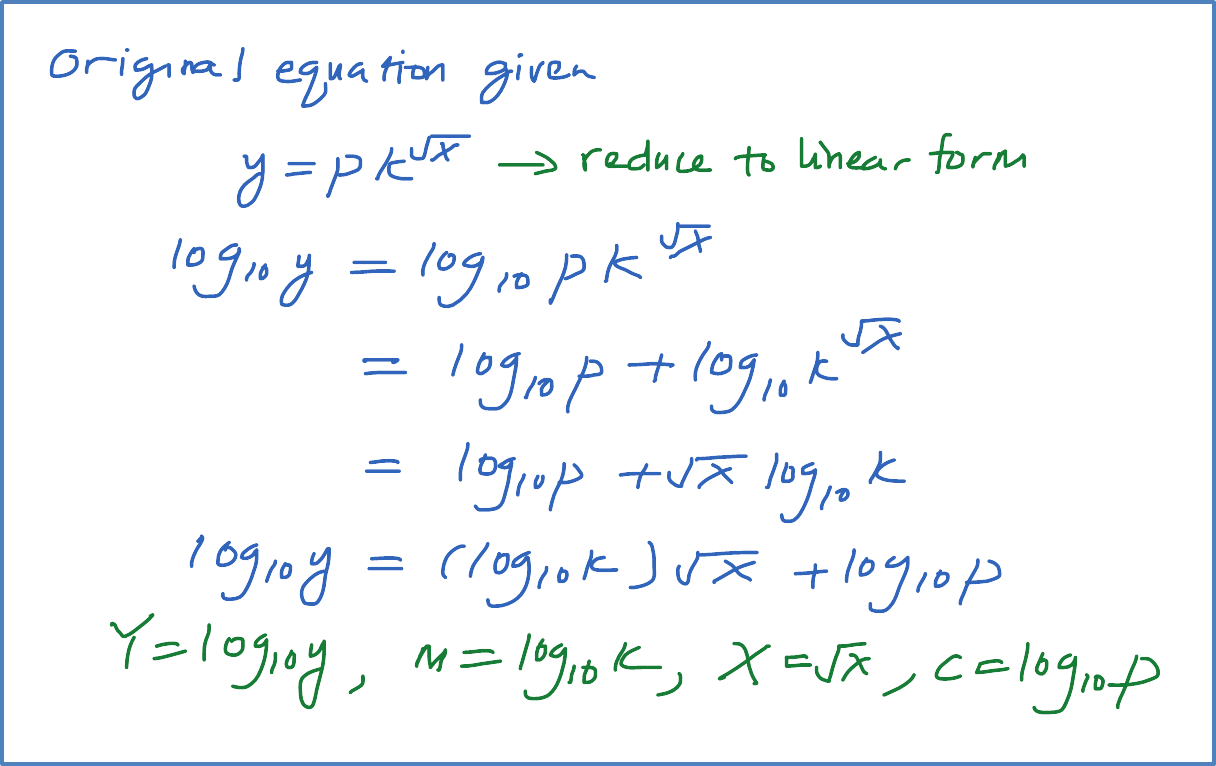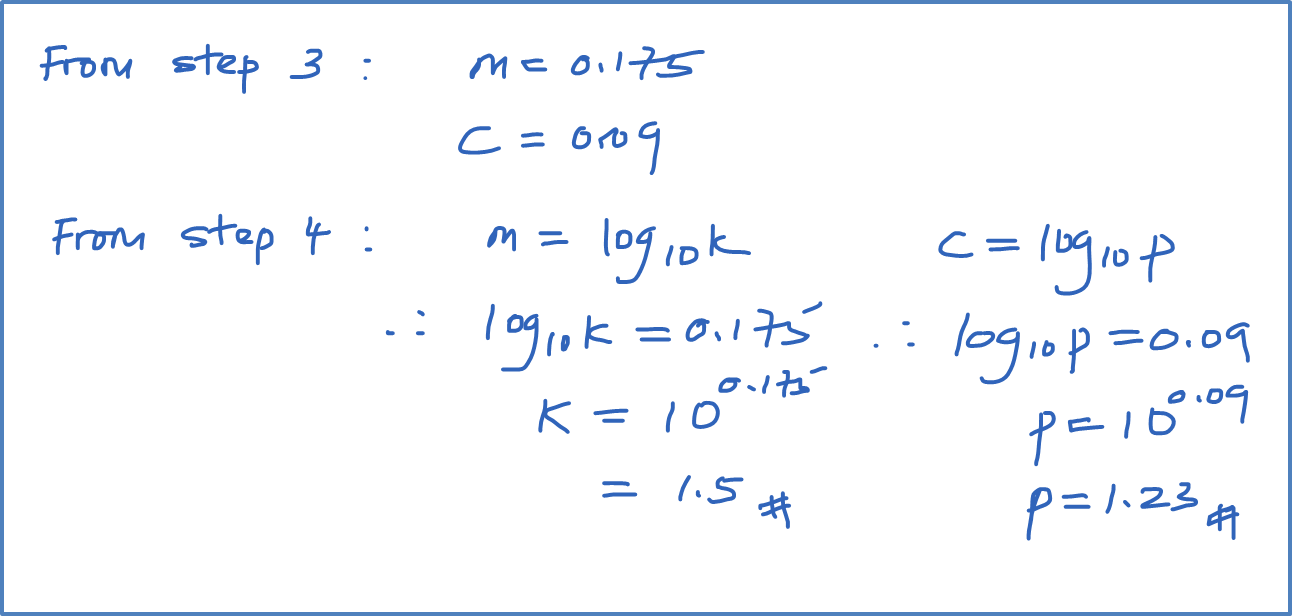Question 9 (12 marks):
The data in the Diagram shows the mass, in g, of 30 strawberries plucked by a tourist from a farm.
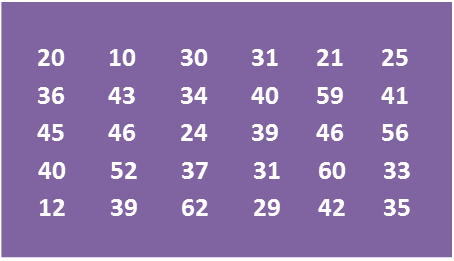 Diagram
Diagram
(a) Based on the Diagram, complete Table 3 in the answer space.
(b) Based on Table, calculate the estimated mean mass of a strawberry.
(c) For this part of the question, use graph paper.
By using the scale of 2 cm to 10 g on the horizontal axis and 2 cm to 1 strawberry on the vertical axis, draw a histogram for the data.
(d) Based on the histogram drawn in 14(c), state the number of strawberries with the mass of more than 50 g.
Answer:

Solution:
(a)

(b)
(c)

(d)
Number of strawberries with the mass more than 50 g
= 3 + 2
= 5
The data in the Diagram shows the mass, in g, of 30 strawberries plucked by a tourist from a farm.
 Diagram
Diagram(a) Based on the Diagram, complete Table 3 in the answer space.
(b) Based on Table, calculate the estimated mean mass of a strawberry.
(c) For this part of the question, use graph paper.
By using the scale of 2 cm to 10 g on the horizontal axis and 2 cm to 1 strawberry on the vertical axis, draw a histogram for the data.
(d) Based on the histogram drawn in 14(c), state the number of strawberries with the mass of more than 50 g.
Answer:

Solution:
(a)

(b)
(c)

(d)
Number of strawberries with the mass more than 50 g
= 3 + 2
= 5
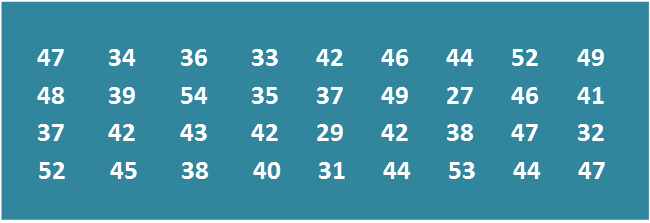 Diagram
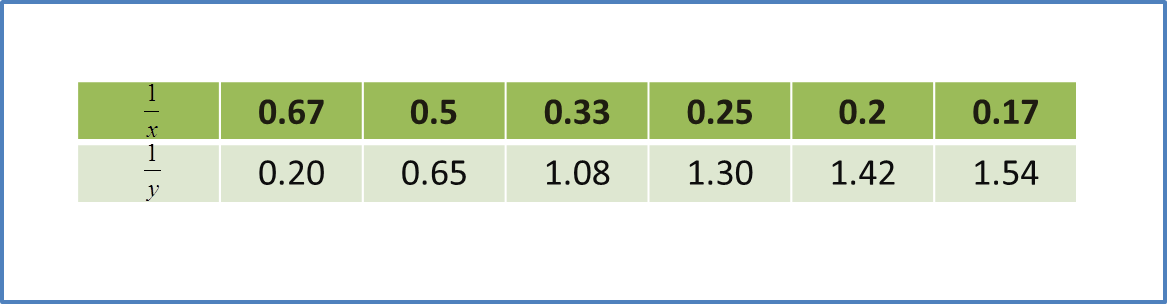
Diagram Table
Table

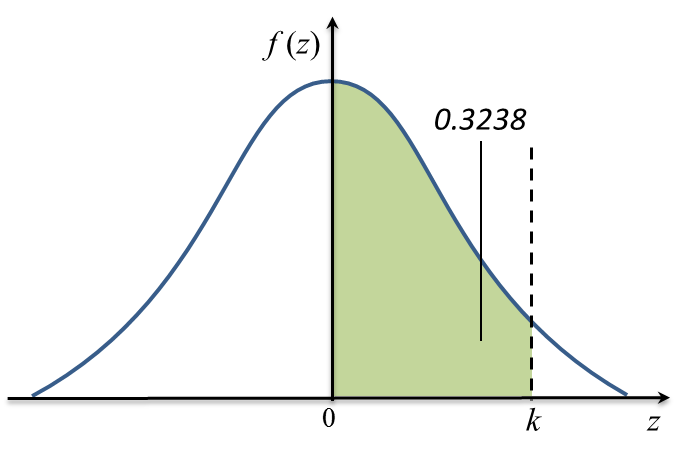

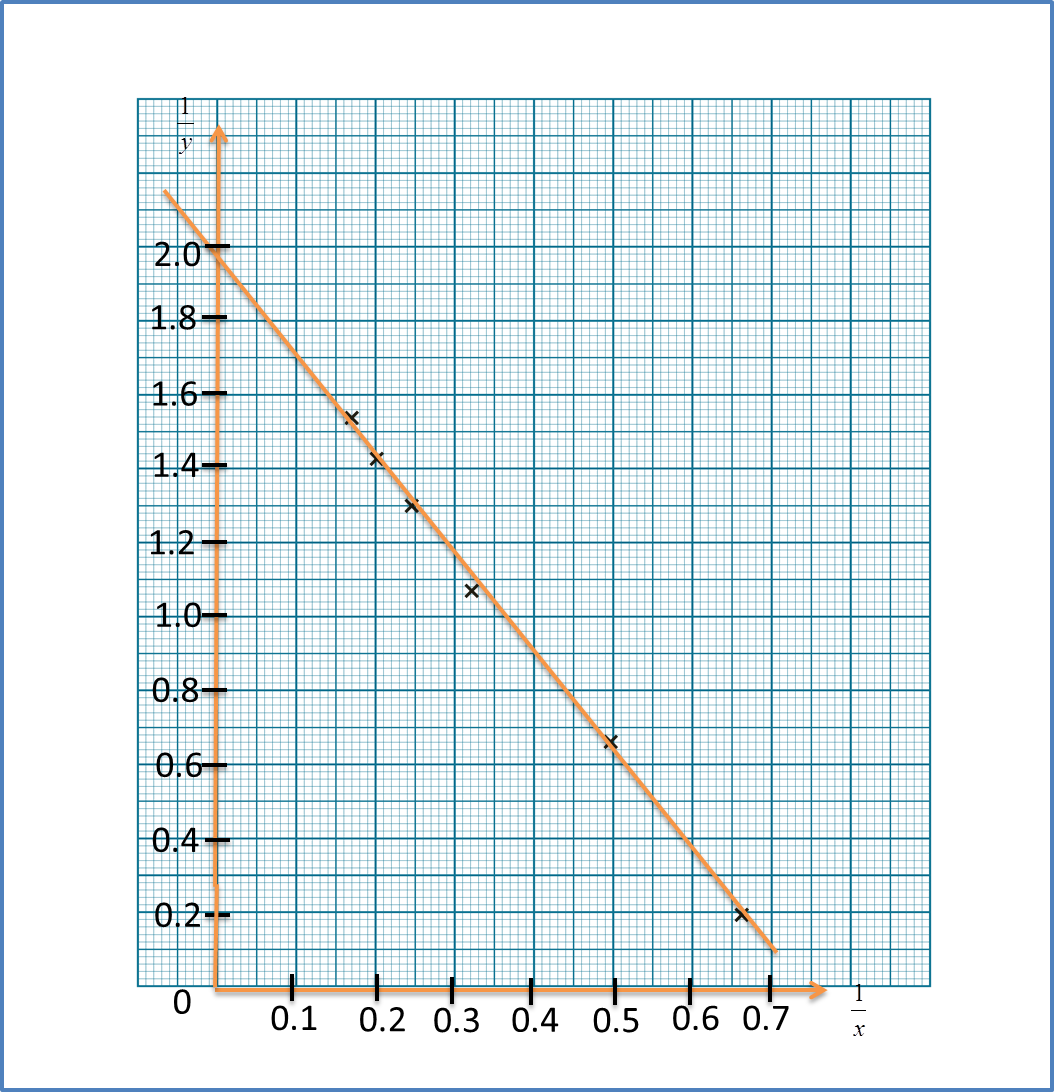
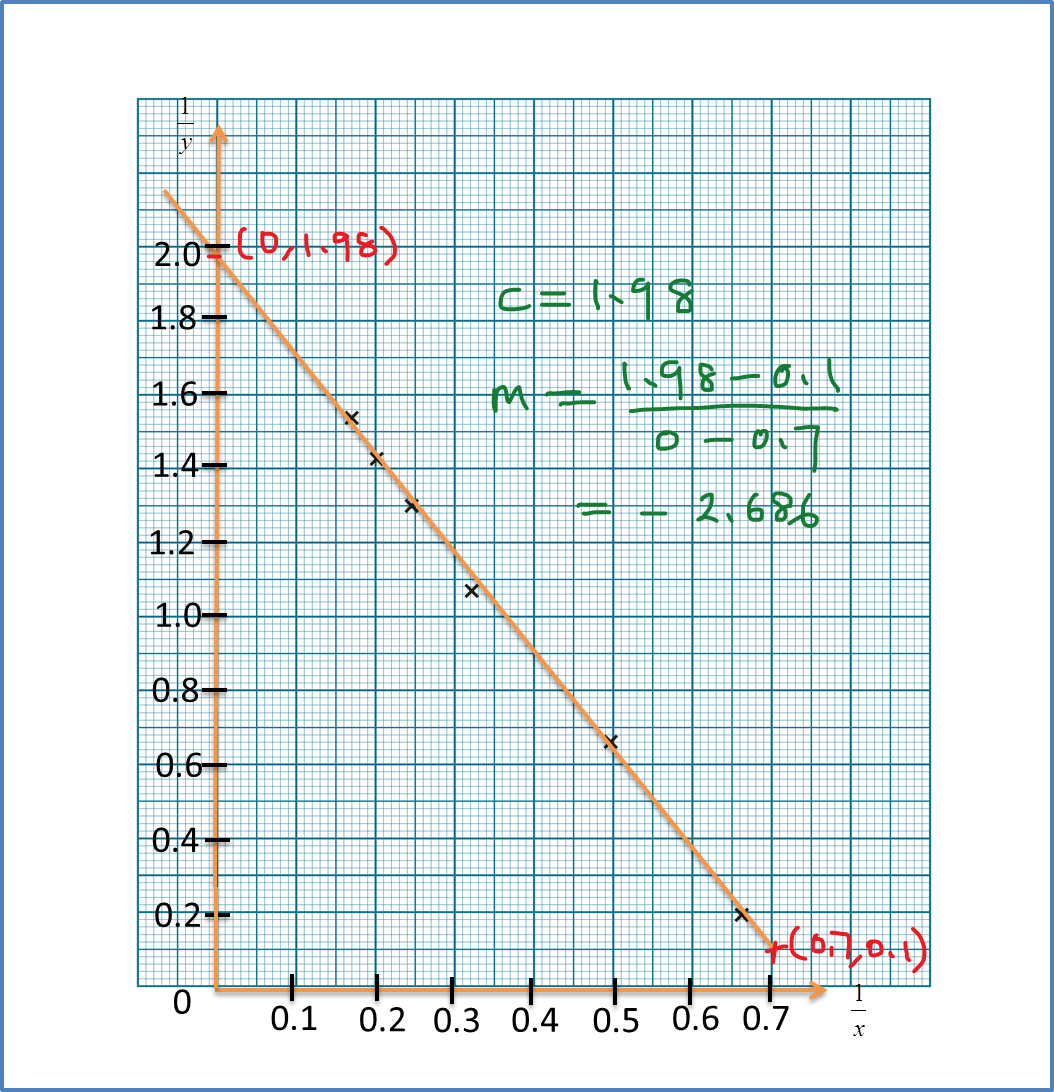
 Diagram 11
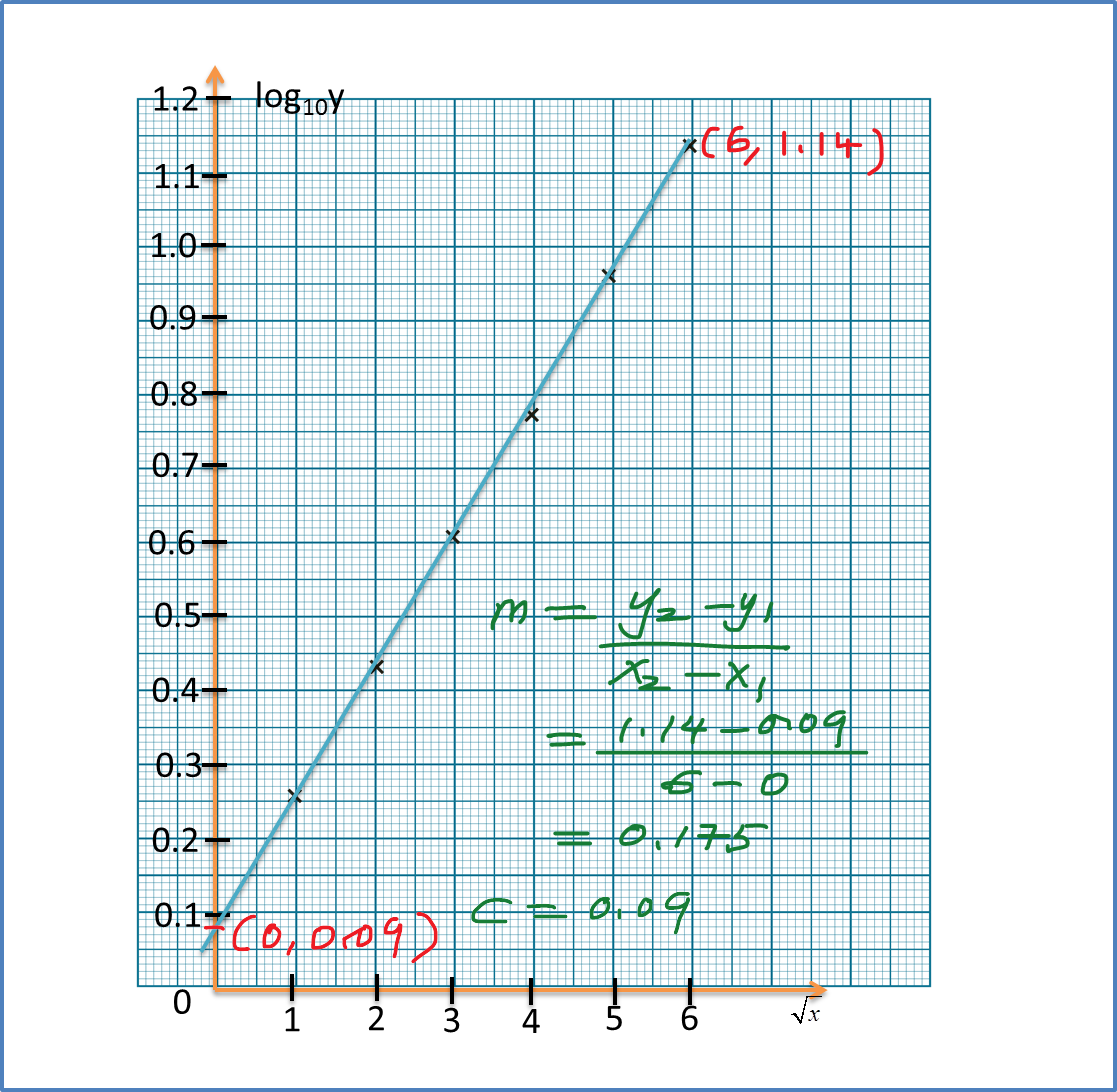
Diagram 11 Diagram 12
Diagram 12