Question 9 (2 marks):
(a) Given C6n>1, list out all the possible values of n.(b) Given Cym=Cyn, express y interms of m and n.
Solution:
(a)
n = 1, 2, 3, 4, 5
(b)
y = m + n
(a) Given C6n>1, list out all the possible values of n.(b) Given Cym=Cyn, express y interms of m and n.
Solution:
(a)
n = 1, 2, 3, 4, 5
(b)
y = m + n
Question 10 (4 marks):
Danya has a home decorations shop. One day, Danya received 14 sets of cups from a supplier. Each set contained 6 pieces of cups of different colours.
(a) Danya chooses 3 sets of cups at random to be checked.
Find the number of different ways that Danya uses to choose those sets of cups.
(b) Danya takes a set of cups to display by arranging it in a row.
Find the number of different ways the cups can be arranged such that the blue cup is not displaced next to the red cup.
Solution:
(a)
Number of different ways 3 sets of cups at random to be checked
= 14C3
=364
(b)

Number of ways (Blue cup and red cup are next to each other)
= 5! × 2!
= 240
Number of different ways the cups can be arranged such that the blue cup is not displaced next to the red cup
= 6! – 240
= 720 – 240
= 480
Danya has a home decorations shop. One day, Danya received 14 sets of cups from a supplier. Each set contained 6 pieces of cups of different colours.
(a) Danya chooses 3 sets of cups at random to be checked.
Find the number of different ways that Danya uses to choose those sets of cups.
(b) Danya takes a set of cups to display by arranging it in a row.
Find the number of different ways the cups can be arranged such that the blue cup is not displaced next to the red cup.
Solution:
(a)
Number of different ways 3 sets of cups at random to be checked
= 14C3
=364
(b)

Number of ways (Blue cup and red cup are next to each other)
= 5! × 2!
= 240
Number of different ways the cups can be arranged such that the blue cup is not displaced next to the red cup
= 6! – 240
= 720 – 240
= 480
 Diagram
Diagram  Diagram
Diagram  Diagram
Diagram 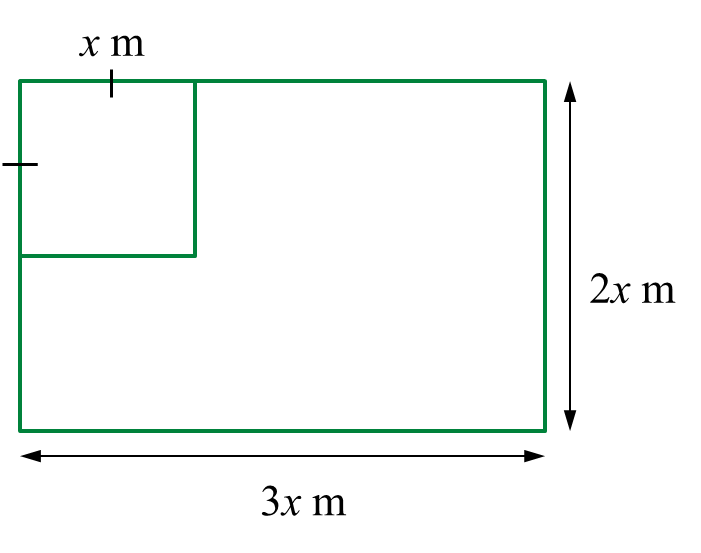
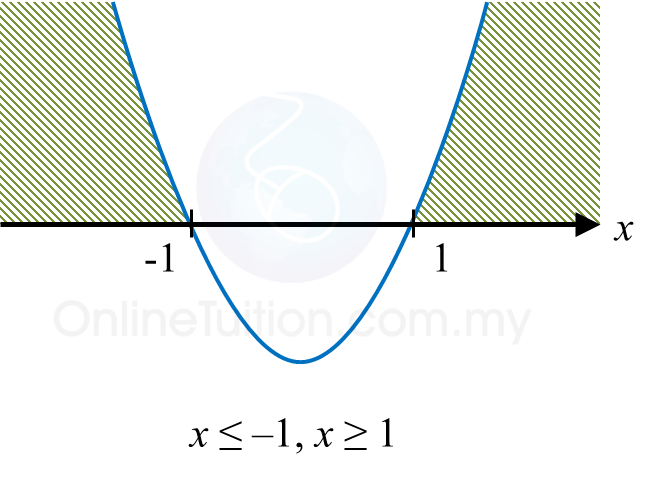
 Diagram 9
Diagram 9
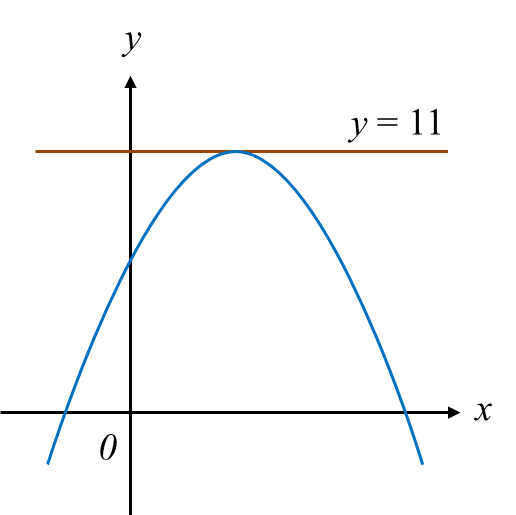 Diagram
Diagram