Soalan 4:
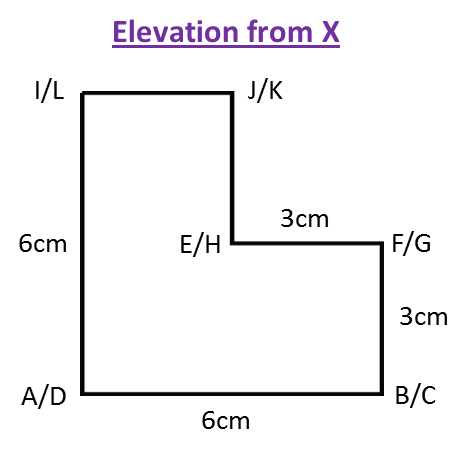
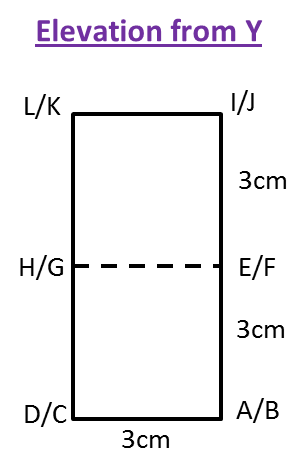
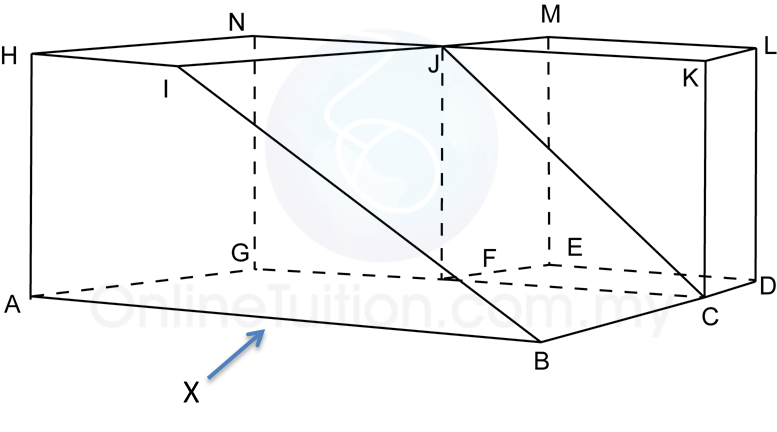
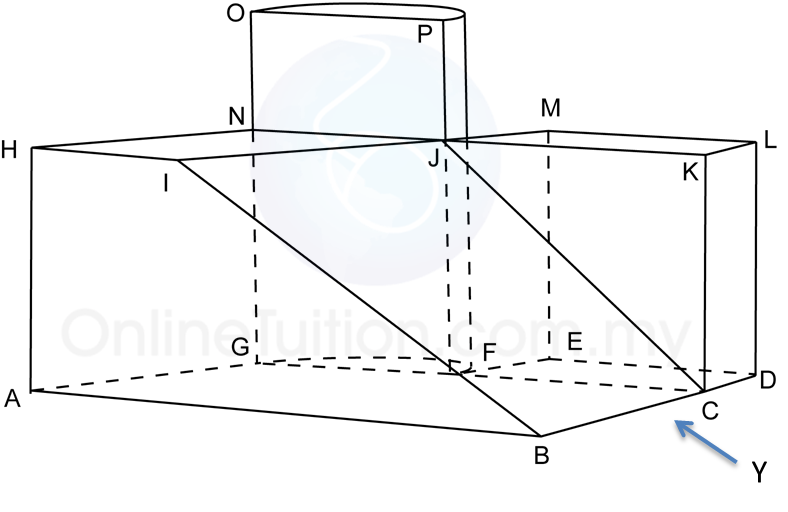
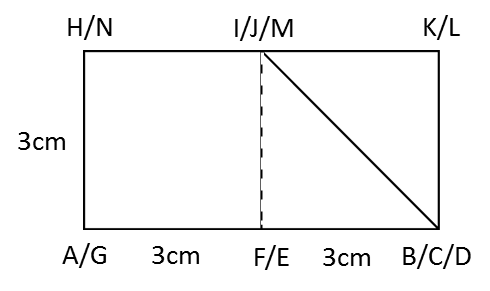
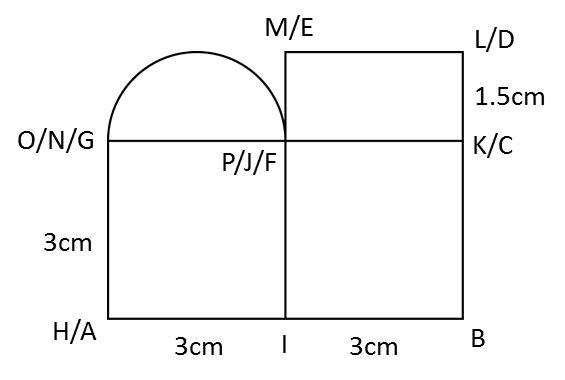
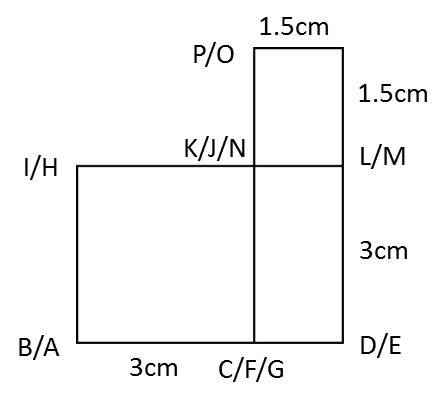
Rajah menunjukkan titik J(1, 2) dan sisi empat ABCD dan sisi empat EFGH, dilukis pada suatu satah Cartes.
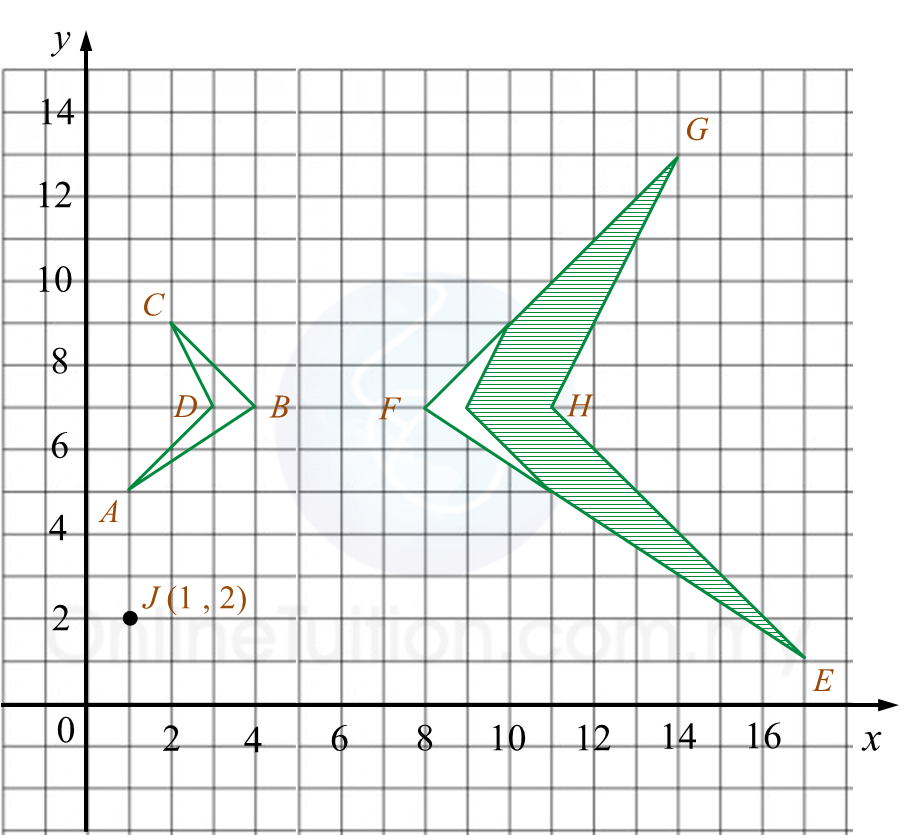
(a) Penjelmaan U ialah satu putaran 90o, ikut arah jam pada pusat O.
Penjelmaan T ialah satu translasi
Penjelmaan R ialah satu pantulan pada garis x = 3.
Nyatakan koordinat imej bagi titik J di bawah setiap penjelmaan berikut:
(i) RU,
(ii) TR.
(b) EFGH ialah imej bagi ABCD di bawah gabungan penjelmaan MN.
Huraikan selengkapnya penjelmaan:
(i) N,
(ii) M.
(c) Diberi bahawa sisi empat ABCD mewakili suatu kawasan yang mempunyai luas 18 m2.
Hitungkan luas, dalam m2, kawasan yang diwakili oleh rantau berlorek.
Penyelesaian:
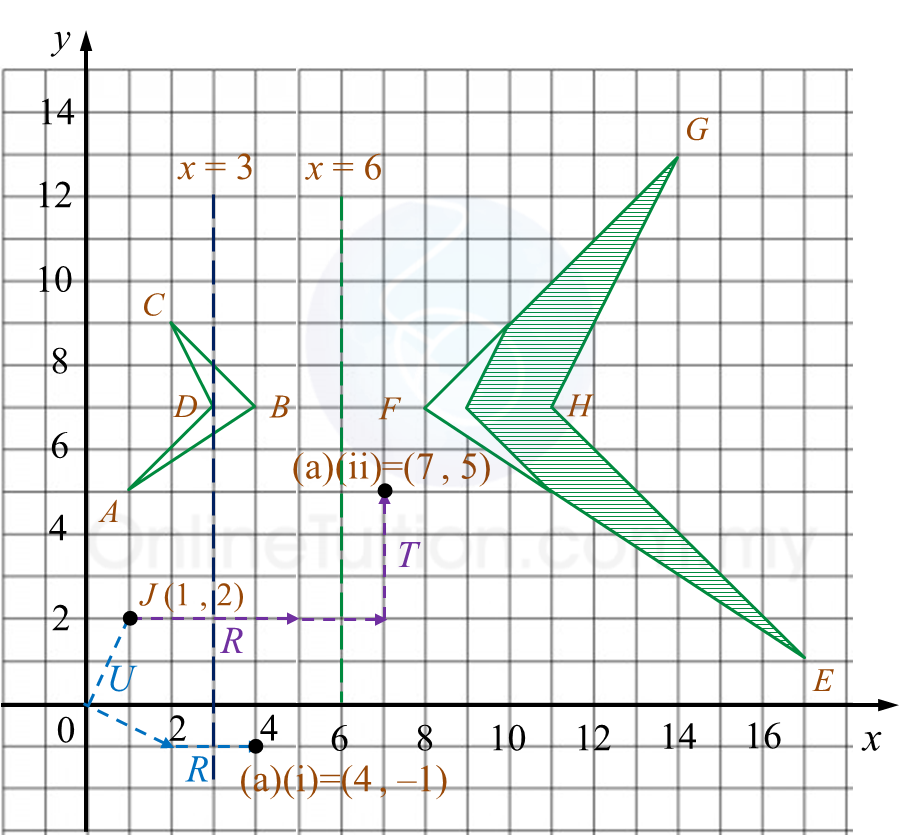
(a)
(i) J (1, 2) → U → (2, –1 ) → R → (4, –1)
(ii) J (1, 2) → R → (5, 2) → T → (7, 5)
(b)(i)
N: Satu pantulan pada garis lurus x = 6.
(b)(ii)
M: Satu pembesaran pada pusat (8, 7) dengan faktor skala 3.
(c)
Luas EFGH = (faktor skala)2 x Luas objek ABCD
= 32 x 18
= 162 m2
Oleh itu,
Luas rantau berlorek
= Luas EFGH – luas ABCD
= 162 – 18
= 144 m2
Rajah menunjukkan titik J(1, 2) dan sisi empat ABCD dan sisi empat EFGH, dilukis pada suatu satah Cartes.

(a) Penjelmaan U ialah satu putaran 90o, ikut arah jam pada pusat O.
Penjelmaan T ialah satu translasi
Penjelmaan R ialah satu pantulan pada garis x = 3.
Nyatakan koordinat imej bagi titik J di bawah setiap penjelmaan berikut:
(i) RU,
(ii) TR.
(b) EFGH ialah imej bagi ABCD di bawah gabungan penjelmaan MN.
Huraikan selengkapnya penjelmaan:
(i) N,
(ii) M.
(c) Diberi bahawa sisi empat ABCD mewakili suatu kawasan yang mempunyai luas 18 m2.
Hitungkan luas, dalam m2, kawasan yang diwakili oleh rantau berlorek.
Penyelesaian:

(a)
(i) J (1, 2) → U → (2, –1 ) → R → (4, –1)
(ii) J (1, 2) → R → (5, 2) → T → (7, 5)
(b)(i)
N: Satu pantulan pada garis lurus x = 6.
(b)(ii)
M: Satu pembesaran pada pusat (8, 7) dengan faktor skala 3.
(c)
Luas EFGH = (faktor skala)2 x Luas objek ABCD
= 32 x 18
= 162 m2
Oleh itu,
Luas rantau berlorek
= Luas EFGH – luas ABCD
= 162 – 18
= 144 m2
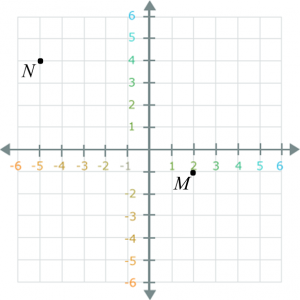

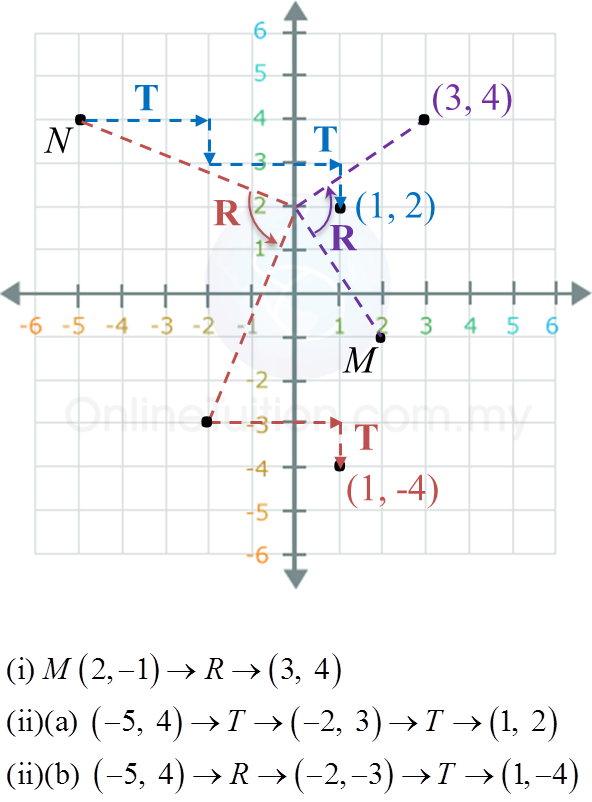
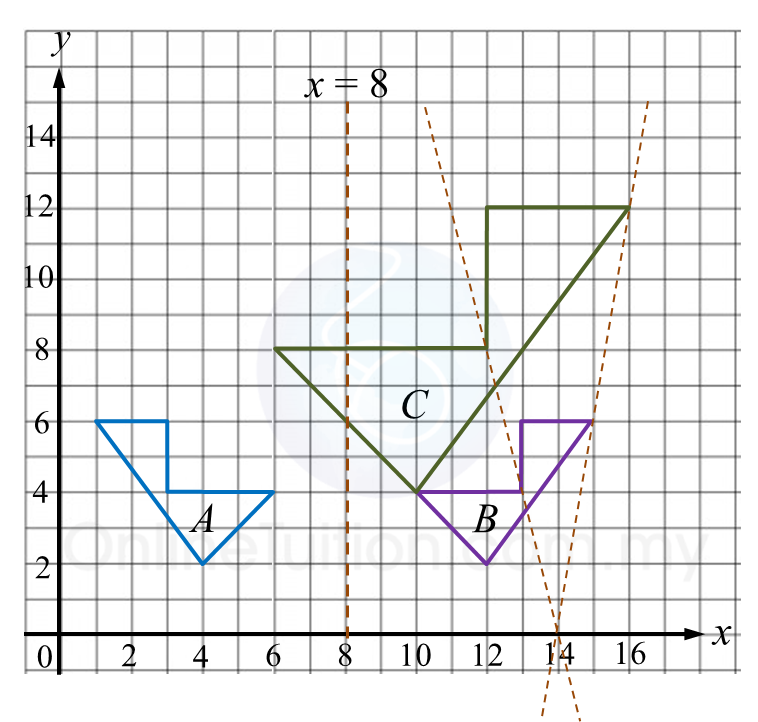
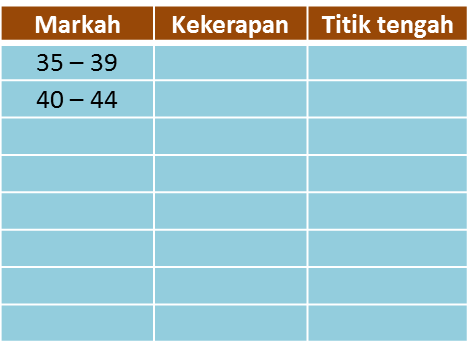
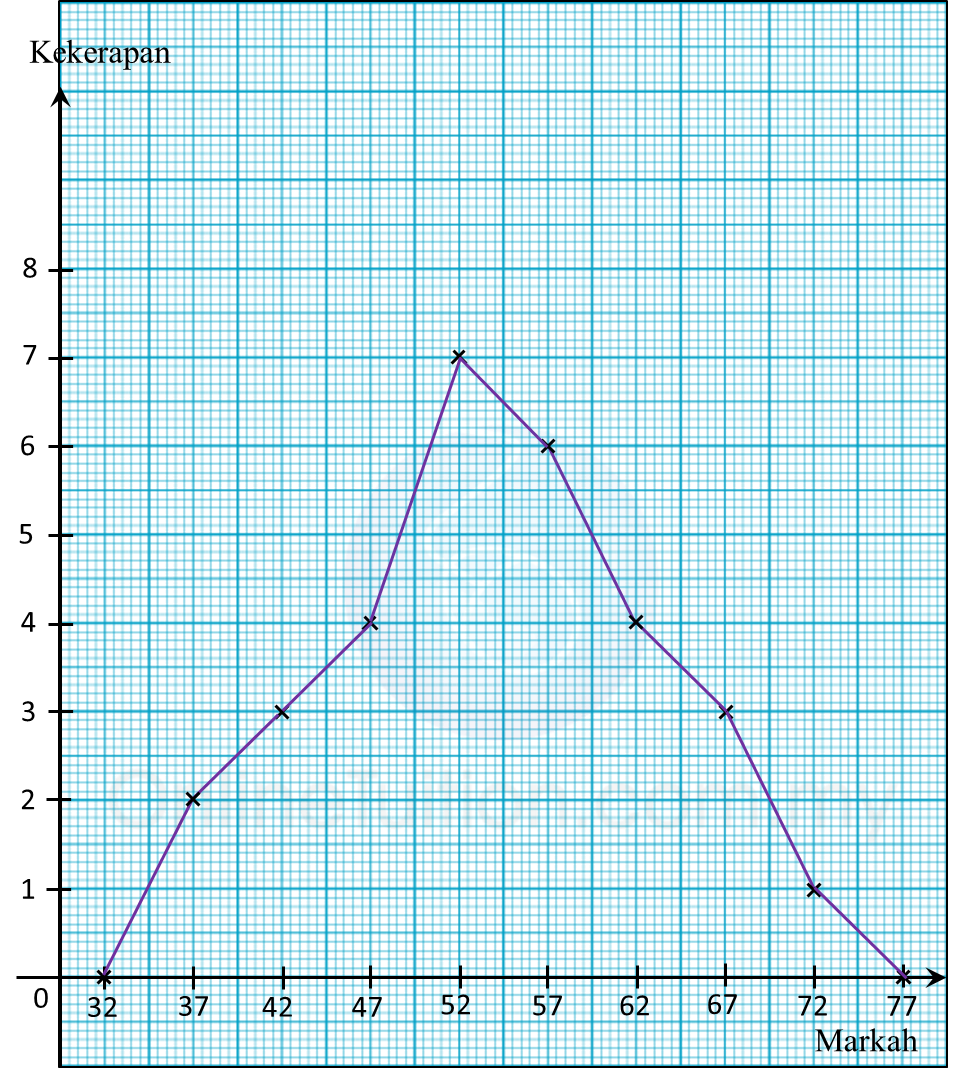
 (a) Berdasarkan data dalam rajah di atas, lengkapkan Jadual di ruang jawapan.
(a) Berdasarkan data dalam rajah di atas, lengkapkan Jadual di ruang jawapan.