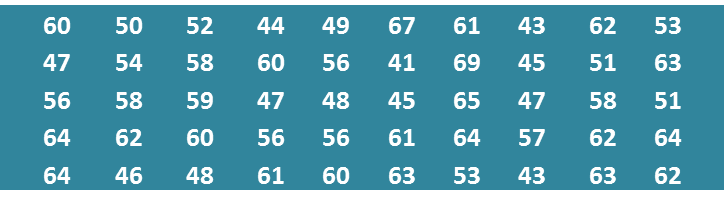
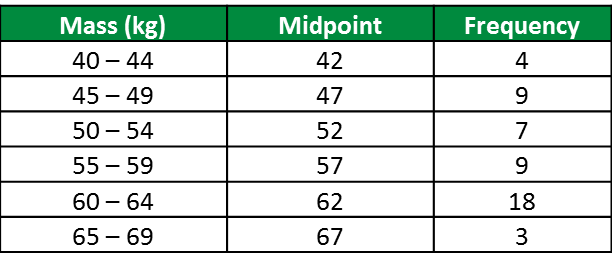
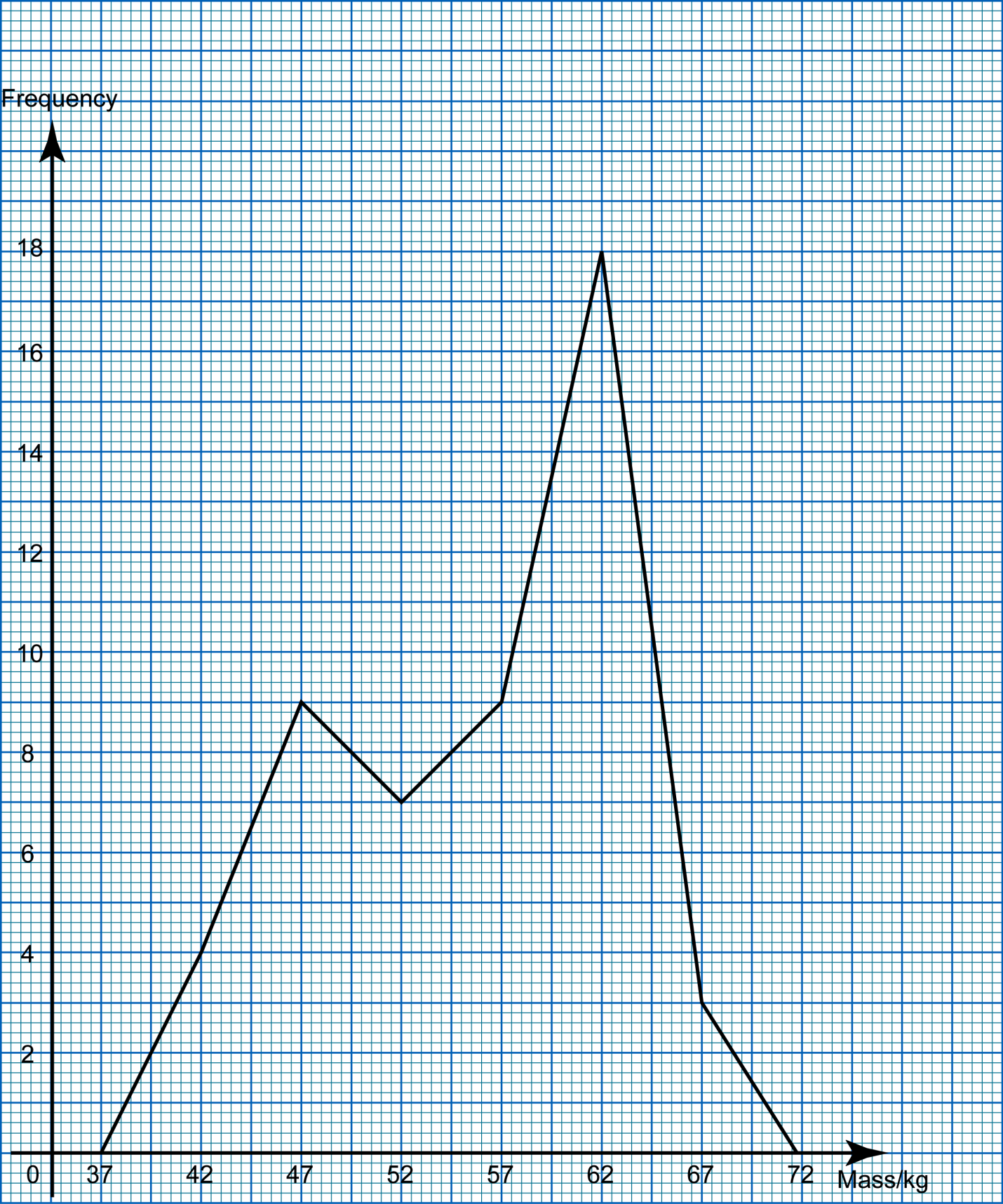
Question 1:
Solution:
Total number of pink marbles = 5 + 4 = 9
Total number of yellow marbles = 21 + 1 = 22
Total number of marbles = 9 + 22 = 31
A box contains 5 pink marbles and 21 yellow marbles. Sharon puts another 4 pink marbles and 1 yellow marble inside the box. A marble is chosen at random from the box.
What is the probability that a pink marble is chosen?
Solution:
Total number of pink marbles = 5 + 4 = 9
Total number of yellow marbles = 21 + 1 = 22
Total number of marbles = 9 + 22 = 31
Question 2:
In a group of 80 prefects, 25 are girls. Then 10 boys leave the group.
If a prefect is chosen at random from the group, state the probability that the prefect chosen is a boy.
Solution:
Number of boys = 80 – 25 = 55
After 10 boys left,
Number of boys = 55 – 10 = 45
Total number of prefects = 25 + 45 = 70
In a group of 80 prefects, 25 are girls. Then 10 boys leave the group.
If a prefect is chosen at random from the group, state the probability that the prefect chosen is a boy.
Solution:
Number of boys = 80 – 25 = 55
After 10 boys left,
Number of boys = 55 – 10 = 45
Total number of prefects = 25 + 45 = 70
Question 3:
60 people have taken part in a singing contest. If a person is chosen at random from all the contestants, the probability of getting a male contestant is . If there are 12 males and 3 females who did not qualify to the second round, find the probability that a male is chosen from the second round contestants.
Solution:
Number of male contestants = 60 × = 32
After 12 males and 3 females left,
Total number of contestants left = 60 – 15 = 45
Number of male contestant = 32 – 12 = 20
60 people have taken part in a singing contest. If a person is chosen at random from all the contestants, the probability of getting a male contestant is . If there are 12 males and 3 females who did not qualify to the second round, find the probability that a male is chosen from the second round contestants.
Solution:
Number of male contestants = 60 × = 32
After 12 males and 3 females left,
Total number of contestants left = 60 – 15 = 45
Number of male contestant = 32 – 12 = 20