(A) Equation of a straight Line
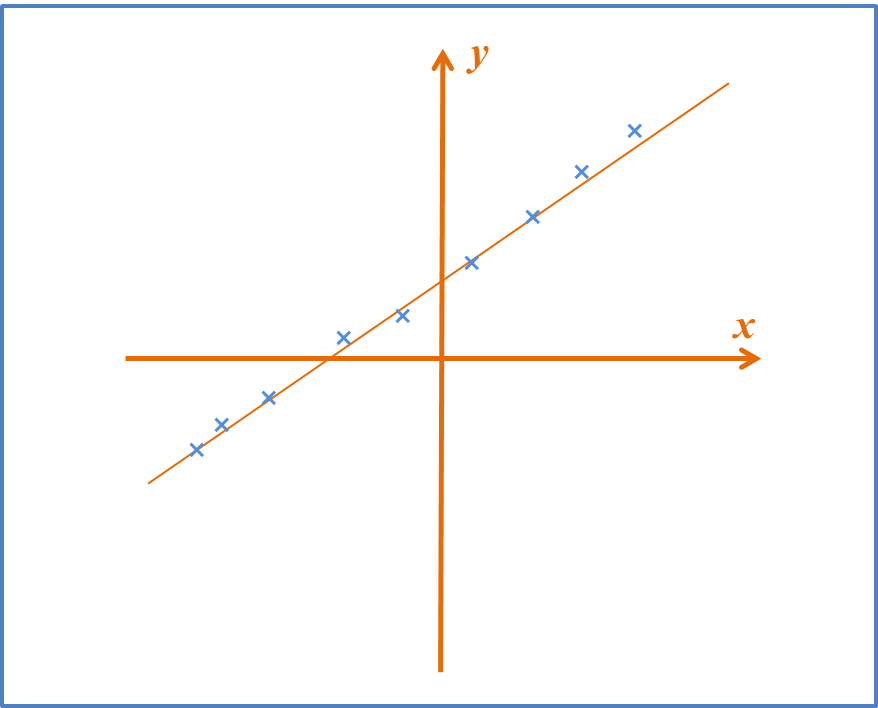
An equation of straight line is given by y = mx + c.
• The variables x and y are linearly related
• The term c is known as y-intercept. It represents the y value where the line cuts the y-axis
• The term m is the gradient of the straight line and its value is constant
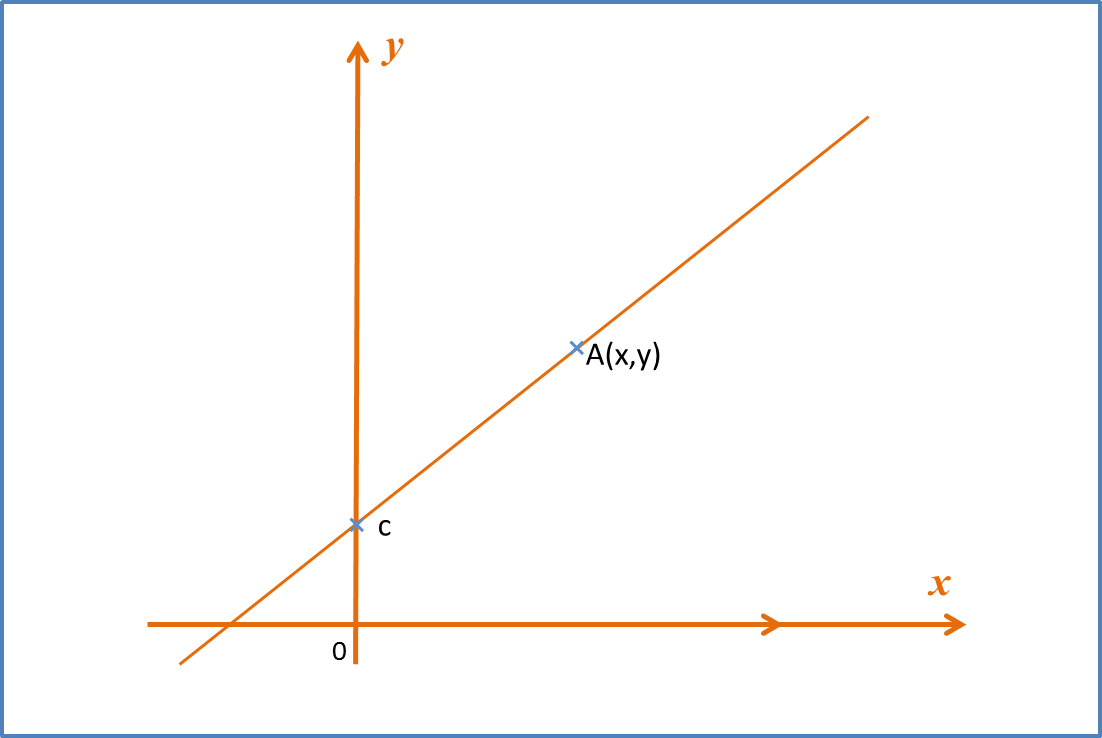
An equation of straight line is given by y = mx + c.
• The variables x and y are linearly related
• The term c is known as y-intercept. It represents the y value where the line cuts the y-axis
• The term m is the gradient of the straight line and its value is constant

(B) Gradient of a Straight Line
If the points and lie on the straight line , then gradient of ,the straight line
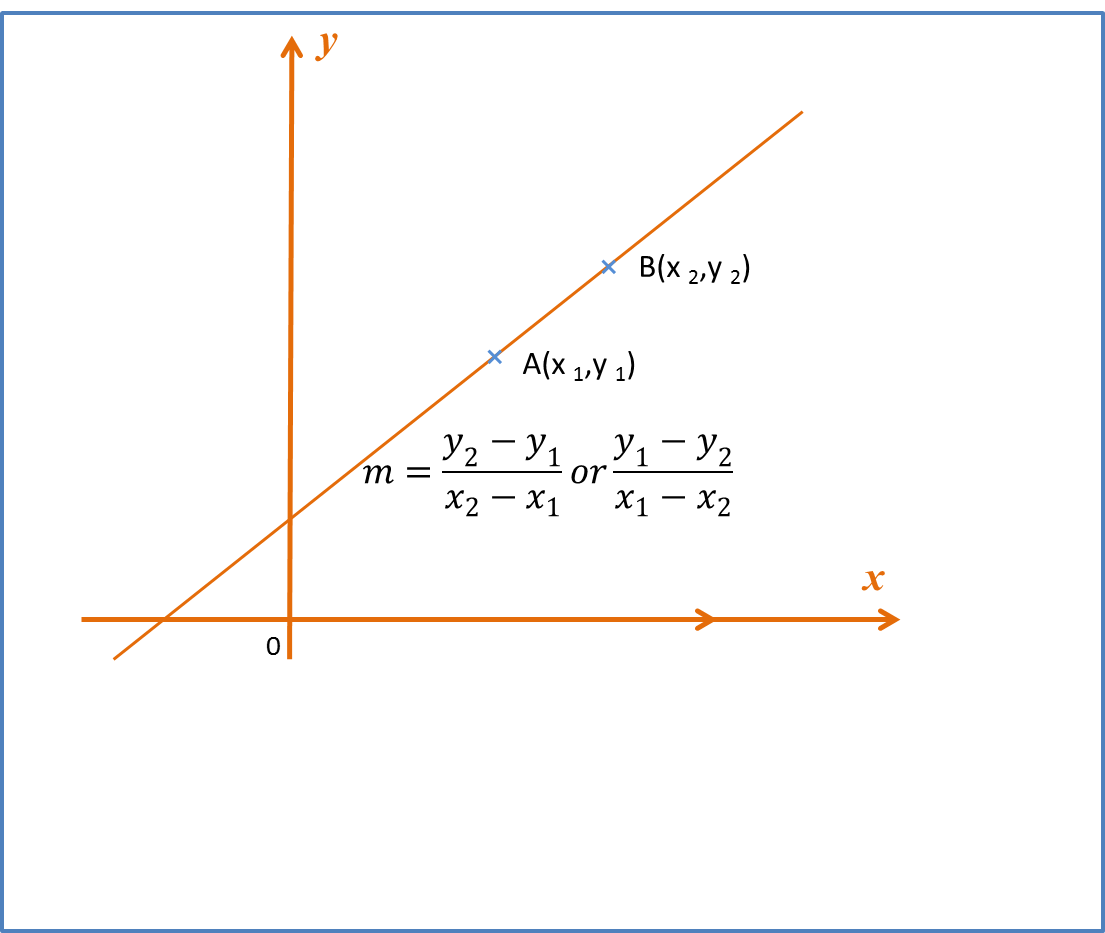
If the points and lie on the straight line , then gradient of ,the straight line

(C) Mid Point
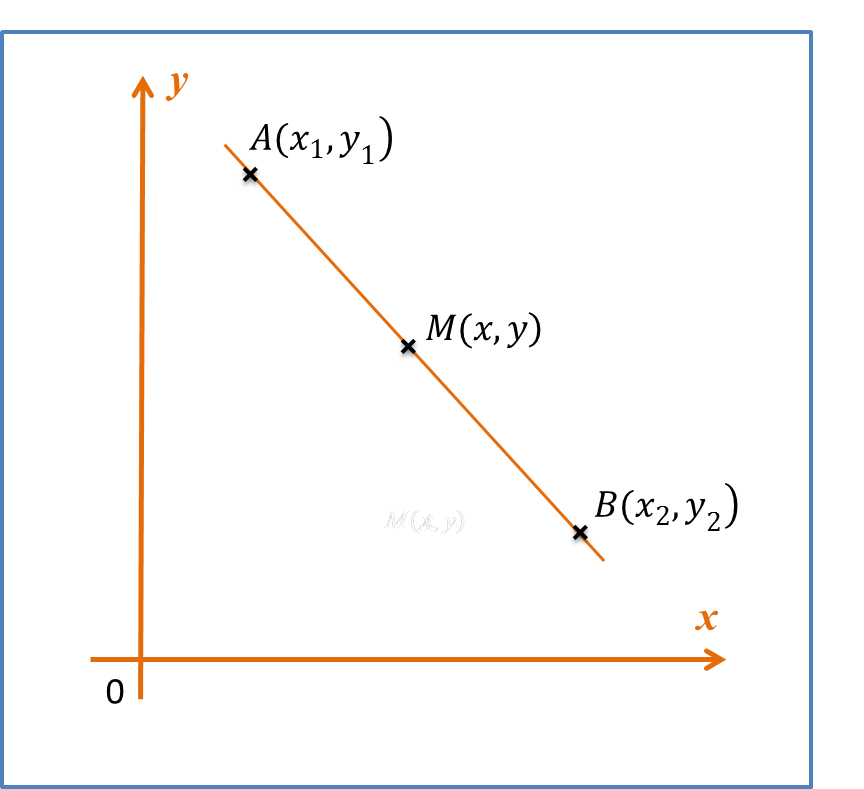
Mid Point AB is given by

Mid Point AB is given by
(D) Distance Between Two Points
Distance between point and point is given by
Distance between point and point is given by