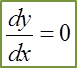Long Questions (Question 1)

Posted on April 22, 2020 by user

Question 1:

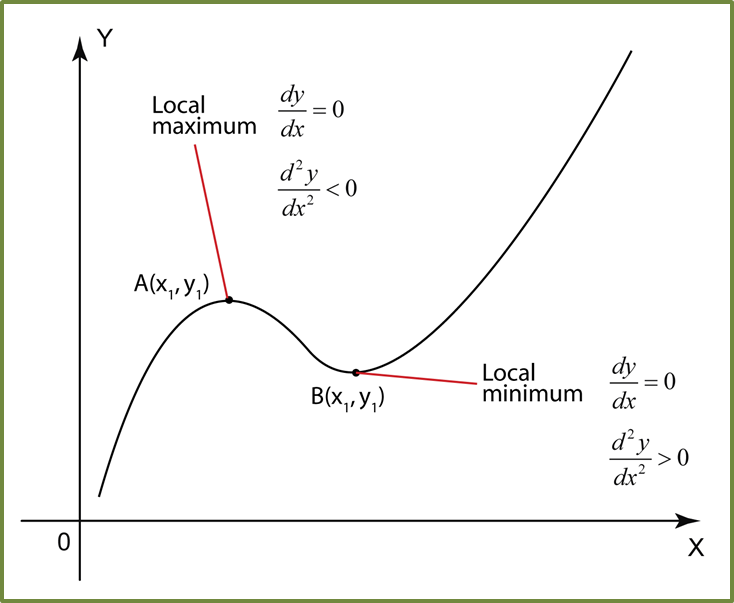
The curve y = x³ – 6x² + 9x + 3 passes through the point P (2, 5) and has two turning points, A (3, 3) and B.

Find

(a) the gradient of the curve at P.

(b) the equation of the normal to the curve at P.

(c) the coordinates of B and determine whether B is a maximum or the minimum point.

Solution:

(a)

y = x³ – 6x² + 9x + 3

dy/dx = 3x²– 12x + 9

At point P (2, 5),

dy/dx = 3(2)² – 12(2) + 9 = –3

Gradient of the curve at point P = –3.

(b)

Gradient of normal at point P = 1/3

Equation of the normal at P (2, 5):

y – y₁= m (x – x₁)

y – 5 = 1/3 (x – 2)

3y – 15 = x – 2

3y = x + 13

(c)

At turning point, dy/dx = 0.

3x² – 12x + 9 = 0

x² – 4x + 3 = 0

(x – 1)( x – 3) = 0

x – 1 = 0 or x – 3 = 0

x = 1 x = 3 (Point A)

Thus at point B:

x = 1

y = (1)³– 6(1)² + 9(1) + 3 = 7

Thus, coordinates of B = (1, 7)

\begin{array}{l} when x = 1, \\ \frac{d^{2} y}{d x^{2}} = 6 x - 12 \\ \frac{d^{2} y}{d x^{2}} = 6 (1) - 12 \\ \frac{d^{2} y}{d x^{2}} = - 6 < 0 \\ Since \frac{d^{2} y}{d x^{2}} < 0, B is a maximum point . \end{array}

Short Questions (Question 22 – 25)

Posted on April 22, 2020 by user

Question 23:

Given that

y = 15 x + \frac{24}{x^{3}}

(a) Find the value of

\frac{d y}{d x}

when x = 2,

(b) Express in terms of k, the approximate change in y when x changes from 2 to

2 + k, where k is a small change.

Solution:
(a)

\begin{array}{l} y = 15 x + \frac{24}{x^{3}} \\ y = 15 x + 24 x^{- 3} \\ \frac{d y}{d x} = 15 - 72 x^{- 4} \\ \frac{d y}{d x} = 15 - \frac{72}{x^{4}} \\ When x = 2 \\ \frac{d y}{d x} = 15 - \frac{72}{2^{4}} = 10.5 \end{array}

(b)

\begin{array}{l} Approximate change in y to x in terms of k, \\ \frac{δ y}{δ x} \approx \frac{d y}{d x} \\ δ y = \frac{d y}{d x} \times δ x \\ δ y = 10.5 \times (2 + k - 2) \\ δ y = 10.5 k \end{array}

Question 24:

If the radius of a circle increases from 4 cm to 4.01 cm, find the approximate increase in the area.

Solution:

\begin{array}{l} Area of circle, A = π r^{2} \\ \frac{d A}{d r} = 2 π r \\ Approximate increase in the area to radius, \\ \frac{δ A}{δ r} \approx \frac{d A}{d r} \\ δ A = \frac{d A}{d r} \times δ r \\ δ A = (2 π r) \times (4.01 - 4) \\ δ A = [2 π (4)] \times (0.01) \\ δ A = 0.08 π {cm}^{2} \end{array}

Question 25:

Given that y =3t+ 5t² and x = 5t –1.

(a) Find

\frac{d y}{d x}

in terms of x,

(b) If x increases from 5 to 5.01, find the small increase in t.

Solution:

\begin{array}{l} y = 3 t + 5 t^{2} \\ \frac{d y}{d t} = 3 + 10 t \\ x = 5 t - 1 \\ \frac{d x}{d t} = 5 \end{array}

(a)

\begin{array}{l} \frac{d y}{d x} = \frac{d y}{d t} \times \frac{d t}{d x} \\ \frac{d y}{d x} = (3 + 10 t) \times \frac{1}{5} \\ \frac{d y}{d x} = \frac{3 + 10 (\frac{x + 1}{5})}{5} \leftarrow \begin{array}{l} x = 5 t - 1 \\ t = \frac{x + 1}{5} \end{array} \\ \frac{d y}{d x} = \frac{3 + 2 x + 2}{5} \\ \frac{d y}{d x} = \frac{5 + 2 x}{5} \end{array}

(b)

\begin{array}{l} Small increase in t to x, \\ δ t = \frac{d t}{d x} \times δ x \\ δ t = \frac{1}{5} \times (5.01 - 5) \\ δ t = 0.002 \end{array}

Short Questions (Question 20 – 22)

Posted on April 22, 2020 by user

Question 20:

The volume of water V cm³, in a container is given by

V = \frac{1}{5} h^{3} + 7 h

, where h cm is the height of the water in the container. Water is poured into the container at the rate of 15cm³s^-1. Find the rate of change of the height of water in cms^-1, at the instant when its height is 3cm.

Solution:

\begin{array}{l} V = \frac{1}{5} h^{3} + 7 h \\ \frac{d V}{d h} = \frac{3}{5} h^{2} + 7 = \frac{3 h^{2} + 35}{5} \\ Given \frac{d V}{d t} = 15, h = 3 \\ Rate of change of the height of water = \frac{d h}{d t} \\ \frac{d h}{d t} = \frac{d h}{d V} \times \frac{d V}{d t} \leftarrow Chain rule \\ \frac{d h}{d t} = \frac{5}{3 h^{2} + 35} \times 15 \\ \frac{d h}{d t} = \frac{75}{62} {cms}^{- 1} \end{array}

Question 21:

A wire of length 88 cm is bent to form a circle. When the wire is heated, the length increases at the rate of 0.3 cms^-1.

(a) Calculate the rate of change in the radius of the circle.

(b) Hence, calculate the radius of the circle after 5s.

Solution:

\begin{array}{l} Length of circumference of a circle, \\ L = 2 π r \\ \frac{d L}{d r} = 2 π \end{array}

(a)

\begin{array}{l} Given \frac{d L}{d t} = 0.3 \\ Rate of change in the radius of the circle = \frac{d r}{d t} \\ \frac{d r}{d t} = \frac{d r}{d L} \times \frac{d L}{d t} \\ \frac{d r}{d t} = \frac{1}{2 π} \times 0.3 \\ \frac{d r}{d t} = 0.0477 {cms}^{- 1} \end{array}

(b)

\begin{array}{l} 2 π r = 88 \\ r = \frac{88}{2 π} = \frac{44}{π} \\ Hence, the radius of the circle after 5 s \\ = \frac{44}{π} + 5 (0.0477) \\ = 14.24 cm \end{array}

Question 22:

The diagram shows a conical container with diameter 0.8m and height 0.6m. Water is poured into the container at a constant rate of 0.02m³s^-1. Calculate the rate of change of the height of the water level when the height of water level is 0.5m.

Solution:

\begin{array}{l} Let, \\ h = height of the water level \\ r = radius of the water surface \\ V = volume of the water \\ \frac{r}{h} = \frac{0.4}{0.6} \leftarrow Concept of similar triangles \\ \frac{r}{h} = \frac{2}{3} \\ r = \frac{2}{3} h \\ Volume of water, V = \frac{1}{3} π r^{2} h \\ V = \frac{1}{3} π {(\frac{2}{3} h)}^{2} h \\ V = \frac{4}{27} π h^{3} \\ \frac{d V}{d h} = (3) \frac{4}{27} π h^{2} \\ \frac{d V}{d h} = \frac{4}{9} π h^{2} \\ The rate of change of the height of the water level \\ when the height of water level is 0 .5 m = \frac{d h}{d t} . \\ \frac{d h}{d t} = \frac{d h}{d V} \times \frac{d V}{d t} \leftarrow Chain rule \\ \frac{d h}{d t} = \frac{9}{4 π h^{2}} \times 0.02 \leftarrow Given \frac{d V}{d t} = 0.02 \\ \frac{d h}{d t} = \frac{9}{4 π {(0.5)}^{2}} \times 0.02 \\ \frac{d h}{d t} = 0.0572 m s^{- 1} \end{array}

Short Questions (Question 14 – 16)

Posted on April 22, 2020 by user

Question 14:

Given y = x (6 – x), express

y \frac{d^{2} y}{d x^{2}} + x \frac{d y}{d x} + 18

in terms of x in the simplest form.

Hence, find the value of x which satisfies the equation

y \frac{d^{2} y}{d x^{2}} + x \frac{d y}{d x} + 18 = 0

Solution:

\begin{array}{l} y = x (6 - x) = 6 x - x^{2} \\ \frac{d y}{d x} = 6 - 2 x \\ \frac{d^{2} y}{d x^{2}} = - 2 \\ ∴ y \frac{d^{2} y}{d x^{2}} + x \frac{d y}{d x} + 18 = (6 x - x^{2}) (- 2) + x (6 - 2 x) + 18 \\ = - 12 x + 2 x^{2} + 6 x - 2 x^{2} + 18 \\ = - 6 x + 18 \\ y \frac{d^{2} y}{d x^{2}} + x \frac{d y}{d x} + 18 = 0 \\ - 6 x + 18 = 0 \\ x = 3 \end{array}

Question 15:

Find the coordinates of the point on the curve, y = (4x – 5)² such that the gradient of the normal to the curve is

\frac{1}{8}

Solution:

y = (4x – 5)²

\frac{d y}{d x}

= 2(4x – 5).4 = 32x – 40

Given the gradient of the normal is 1/8, therefore the gradient of the tangent is –8.

\frac{d y}{d x}

= –8

32x – 40 = –8

32x = 32

x = 1

y = (4(1) – 5)²= 1

Hence, the coordinates of the point on the curve, y = (4x – 5)² is (1, 1).

Question 16:

A curve has a gradient function of kx² – 7x, where k is a constant. The tangent to the curve at the point (1, 4) is parallel to the straight line y + 2x–1 = 0. Find the value of k.

Solution:

Gradient function of kx²– 7x is parallel to the straight line y + 2x–1 = 0

\frac{d y}{d x}

= kx²– 7x

y + 2x –1 = 0, y = –2x + 1, gradient of the straight line = –2

Therefore kx²– 7x = –2

At the point (1, 4),

k(1)² – 7(1) = –2

k – 7 = –2

k = 5

Short Questions (Question 11 – 13)

Posted on April 22, 2020 by user

Question 11:
Given that the graph of function

f (x) = h x^{3} + \frac{k}{x^{2}}

has a gradient function

f' (x) = 12 x^{2} - \frac{258}{x^{3}}

such that h and k are constants. Find the values of h and k.

Solution:

\begin{array}{l} f (x) = h x^{3} + \frac{k}{x^{2}} = h x^{3} + k x^{- 2} \\ f' (x) = 3 h x^{2} - 2 k x^{- 3} \\ f' (x) = 3 h x^{2} - \frac{2 k}{x^{3}} \\ But it is given that f' (x) = 12 x^{2} - \frac{258}{x^{3}} \\ Hence, by comparison, \\ 3 h = 12 and          2 k = 258 \\ h = 4 k = 129 \end{array}

Question 12:

\begin{array}{l} Given that y = \frac{x^{2}}{x + 3}, show that \frac{d y}{d x} = \frac{x^{2} + 6 x}{{(x + 3)}^{2}} \\ Find \frac{d^{2} y}{d x^{2}} in the simplest form . \end{array}

Solution:

\begin{array}{l} y = \frac{x^{2}}{x + 3} \\ \frac{d y}{d x} = \frac{(x + 3) (2 x) - x^{2} .1}{{(x + 3)}^{2}} = \frac{2 x^{2} + 6 x - x^{2}}{{(x + 3)}^{2}} \\ \frac{d y}{d x} = \frac{x^{2} + 6 x}{{(x + 3)}^{2}} (shown) \\ \frac{d^{2} y}{d x^{2}} = \frac{{(x + 3)}^{2} (2 x + 6) - (x^{2} + 6 x) .2 (x + 3)}{{(x + 3)}^{4}} \\ \frac{d^{2} y}{d x^{2}} = \frac{(x + 3) [(x + 3) (2 x + 6) - 2 (x^{2} + 6 x)]}{{(x + 3)}^{4}} \\ \frac{d^{2} y}{d x^{2}} = \frac{[2 x^{2} + 6 x + 6 x + 18 - 2 x^{2} - 12 x]}{{(x + 3)}^{3}} \\ \frac{d^{2} y}{d x^{2}} = \frac{18}{{(x + 3)}^{3}} \end{array}

Question 13:

If y = x^{2} + 4 x, show that x^{2} \frac{d^{2} y}{d x^{2}} - 2 x \frac{d y}{d x} + 2 y = 0.

Solution:

\begin{array}{l} y = x^{2} + 4 x \\ \frac{d y}{d x} = 2 x + 4 \\ \frac{d^{2} y}{d x^{2}} = 2 \\ x^{2} \frac{d^{2} y}{d x^{2}} - 2 x \frac{d y}{d x} + 2 y \\ = x^{2} (2) - 2 x (2 x + 4) + 2 (x^{2} + 4 x) \\ = 2 x^{2} - 4 x^{2} - 8 x + 2 x^{2} + 8 x \\ = 0 (Shown) \end{array}

Short Questions (Question 5 – 7)

Posted on April 22, 2020 by user

Question 5:

Given that f (x) = 3x²(4x²– 1)⁷, find f’(x).

Solution:

f (x) = 3x²(4x²– 1)⁷

f’(x) = 3x². 7(4x²– 1)⁶. 8x + (4x²– 1)⁷. 6x

f’(x) = 168x³ (4x²– 1)⁶ + 6x (4x²– 1)⁷

f’(x) = 6x (4x²– 1)⁶ [28x²+ (4x²– 1)]

f’(x) = 6x (4x²– 1)⁶ (32x²– 1)

Question 6:

Given that y = (1 + 4x)³(3x²– 1)⁴, find

\frac{d y}{d x}

Solution:

y = (1 + 4x)³(3x²– 1)⁴

\frac{d y}{d x}

= (1 + 4x)³. 4(3x²– 1)³.6x + (3x²– 1)⁴. 3(1 + 4x)².4

= 24x (1 + 4x)³(3x²– 1)³ + 12 (3x² – 1)⁴(1 + 4x)²

= 12 (1 + 4x)²(3x²– 1)³ [2x (1 + 4x) + (3x²– 1)]

= 12 (1 + 4x)²(3x²– 1)³ [2x + 8x² + 3x²– 1]

= 12 (1 + 4x)²(3x²– 1)³ [11x² + 2x – 1]

Question 7:

Given that f (x) = 3 x \sqrt{4 x^{2} - 1}, find f' (x) .

.

Solution:

\begin{array}{l} f (x) = 3 x \sqrt{4 x^{2} - 1} = 3 x {(4 x^{2} - 1)}^{\frac{1}{2}} \\ f' (x) = 3 x . \frac{1}{2} {(4 x^{2} - 1)}^{- \frac{1}{2}} .8 x + {(4 x^{2} - 1)}^{\frac{1}{2}} .3 \\ f' (x) = 12 x^{2} {(4 x^{2} - 1)}^{- \frac{1}{2}} + 3 {(4 x^{2} - 1)}^{\frac{1}{2}} \\ f' (x) = 3 {(4 x^{2} - 1)}^{- \frac{1}{2}} [4 x^{2} + (4 x^{2} - 1)] \\ f' (x) = \frac{3 (8 x^{2} - 1)}{\sqrt{(4 x^{2} - 1)}} \end{array}

Short Questions (Question 1 – 4)

Posted on April 22, 2020 by user

Question 1:

Differentiate the expression 2x (4x² + 2x – 5) with respect to x.

Solution:

2x (4x² + 2x – 5) = 8x³ + 4x²– 10x

\frac{d}{d x}

(8x³ + 4x² – 10x)

= 24x + 8x –10

Question 2:

Given that y = \frac{x^{3} + 2 x^{2} + 1}{3 x}, find \frac{d y}{d x} .

.

Solution:

\begin{array}{l} y = \frac{x^{3} + 2 x^{2} + 1}{3 x} \\ y = \frac{x^{3}}{3 x} + \frac{2 x^{2}}{3 x} + \frac{1}{3 x} \\ y = \frac{x^{2}}{3} + \frac{2 x}{3} + \frac{1}{3} x^{- 1} \\ \frac{d y}{d x} = \frac{2 x}{3} + \frac{2}{3} - \frac{1}{3} x^{- 2} \\ \frac{d y}{d x} = \frac{2 x}{3} + \frac{2}{3} - \frac{1}{3 x^{2}} \end{array}

Question 3:

Given that y = \frac{3}{\sqrt{5 x + 1}}, find \frac{d y}{d x}

Solution:

\begin{array}{l} y = \frac{3}{\sqrt{5 x + 1}} = 3 {(5 x + 1)}^{- \frac{1}{2}} \\ \frac{d y}{d x} = - \frac{1}{2} .3 {(5 x + 1)}^{- \frac{3}{2}} (5) \\ \frac{d y}{d x} = \frac{- 15}{2 {[{(5 x + 1)}^{3}]}^{\frac{1}{2}}} \\ \frac{d y}{d x} = \frac{- 15}{2 \sqrt{{(5 x + 1)}^{3}}} \end{array}

Question 4:

Given that

y = \frac{3}{5} u^{5}

, where u = 4x + 1. Find

\frac{d y}{d x}

in terms of x.

Solution:

\begin{array}{l} y = \frac{3}{5} u^{5}, u = 4 x + 1 \\ y = \frac{3}{5} {(4 x + 1)}^{5} \\ \frac{d y}{d x} = 5. \frac{3}{5} {(4 x + 1)}^{4} .4 \\ \frac{d y}{d x} = 12 {(4 x + 1)}^{4} \end{array}

9.9 Small Changes and Approximations

Posted on April 22, 2020 by user

[adinserter block="3"]

9.9 Small Changes and Approximations

If δ x is very small, \frac{δ y}{δ x} will be a good approximation of \frac{d y}{d x},

This is very useful information in determining an approximation of the change in one variable given the small change in the second variable.

[adinserter block="3"]

Example:

Given that y = 3x² + 2x – 4. Use differentiation to find the small change in y when x increases from 2 to 2.02.

Solution:

\begin{array}{l} y = 3 x^{2} + 2 x - 4 \\ \frac{d y}{d x} = 6 x + 2 \end{array}

The small change in y is denoted by δy while the small change in the second quantity that can be seen in the question is the x and is denoted by δx.

\begin{array}{l} \frac{δ y}{δ x} \approx \frac{d y}{d x} \\ δ y = \frac{d y}{d x} \times δ x \\ δ y = (6 x + 2) \times (2.02 - 2) \to δ x = new x - original x \\ δ y = [6 (2) + 2] \times 0.02 \\ Substitute x with the original value of x, i .e . 2. \\ δ y = 0.28 \end{array}

Related Rates of Change

Posted on April 22, 2020 by user

(A) Related Rates of Change

1. If two variables x and y are connected by the equation y = f(x)

Notes:

If x changes at the rate of 5 cms ^-1⇒

\frac{d x}{d t} = 5

Decreases/leaks/reduces Þ NEGATIVES values!!!

Example 1 (Rate of change of y and x)

Two variables, x and y are related by the equation

y = 4 x + \frac{3}{x}

. Given that y increases at a constant rate of 2 units per second, find the rate of change of x when x = 3.

Solution:

\begin{array}{l} y = 4 x + \frac{3}{x} = 4 x + 3 x^{- 1} \\ \frac{d y}{d x} = 4 - 3 x^{- 2} = 4 - \frac{3}{x^{2}} \\ \frac{d y}{d t} = \frac{d y}{d x} \times \frac{d x}{d t} \\ 2 = (4 - \frac{3}{x^{2}}) \times \frac{d x}{d t} \\ when x = 3 \\ 2 = (4 - \frac{3}{3^{2}}) \times \frac{d x}{d t} \\ 2 = \frac{11}{3} \times \frac{d x}{d t} \\ \frac{d x}{d t} = \frac{6}{11} unit s^{- 1} \end{array}

(B) Rates of Change of Volume, Area, Radius, Height and Length

(C) Rate of Change of Any Combination of Two Variables

9.7 Second-Order Differentiation, Turning Points, Maximum and Minimum Points

Posted on April 22, 2020 by user

(A) Second-Order Differentiation

1. When a function y = x³+ x²– 3x + 6 is differentiated with respect to x, the derivative

\frac{d y}{d x} = 3 x^{2} + 2 x - 3

2. The second function

\frac{d y}{d x}

can be differentiated again with respect to x. This is called the second derivative of y with respect to x and can be written as

\frac{d^{2} y}{d x^{2}}

3. Take note that

\frac{d^{2} y}{d x^{2}} \neq {(\frac{d y}{d x})}^{2}

For example,

If y = 4x³ – 7x² + 5x – 1,

The first derivative

\frac{d y}{d x} = 12 x^{2} - 14 x + 5

The second derivative

\frac{d^{2} y}{d x^{2}} = 24 x - 14

(B) Turning Points, Maximum and Minimum Points

(a) At Turning Points A and B,

(b) At Maximum Point A,

(c) At Minimum Point B,