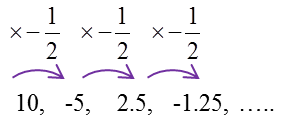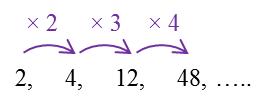Soalan 9 (4 markah):
Diberi bahawa p, 2 dan q ialah tiga sebutan pertama bagi suatu janjang geometri.
Ungkapkan dalam sebutan q
(a) sebutan pertama dan nisbah sepunya janjang itu.
(b) hasil tambah sebutan hingga ketakterhinggaan janjang itu.
Penyelesaian:
(a)
T1=p, T2=2, T3=qT2T1=T3T22p=q2p=4qSebutan pertama, T1=p=4qNisbah sepunya=q2
(b)
a=4q, r=q2S∞=a1−r=4q1−q2=4q÷[1−q2]=4q÷[2−q2]=4q×22−q=82q−q2
Diberi bahawa p, 2 dan q ialah tiga sebutan pertama bagi suatu janjang geometri.
Ungkapkan dalam sebutan q
(a) sebutan pertama dan nisbah sepunya janjang itu.
(b) hasil tambah sebutan hingga ketakterhinggaan janjang itu.
Penyelesaian:
(a)
T1=p, T2=2, T3=qT2T1=T3T22p=q2p=4qSebutan pertama, T1=p=4qNisbah sepunya=q2
(b)
a=4q, r=q2S∞=a1−r=4q1−q2=4q÷[1−q2]=4q÷[2−q2]=4q×22−q=82q−q2
Soalan 10 (3 markah):
Seorang murid mempunyai seutas dawai dengan panjang 13.16 m. Murid itu membahagikan dawai itu kepada beberapa bahagian. Setiap bahagian akan membentuk satu segi empat sama. Rajah menunjukkan tiga buah segi empat sama yang pertama yang dibentuk oleh murid itu.

Rajah
Berapa buah segi empat sama yang boleh dibentuk oleh murid itu?
Penyelesaian:
Perimeter segi empat sama;T1=4(4)=16 cmT2=4(7)=28 cmT3=4(10)=40 cmSebutan pertama, a=16,Beza sepunya, d=28−16=12Jumlah perimeter, Sn=13.16 m=1316 cmn2[2(16)+(n−1)12]=1316n[32+12n−12]=263212n2+20n−2632=03n2+5n−658=0(n−14)(3n+47)=0n−14=0n=14Atau3n+47=0n=−473 (ditolak)14 buah segi empat sama boleh dibentuk dengan menggunakan dawai 13.16 m.
Seorang murid mempunyai seutas dawai dengan panjang 13.16 m. Murid itu membahagikan dawai itu kepada beberapa bahagian. Setiap bahagian akan membentuk satu segi empat sama. Rajah menunjukkan tiga buah segi empat sama yang pertama yang dibentuk oleh murid itu.

Rajah
Berapa buah segi empat sama yang boleh dibentuk oleh murid itu?
Penyelesaian:
Perimeter segi empat sama;T1=4(4)=16 cmT2=4(7)=28 cmT3=4(10)=40 cmSebutan pertama, a=16,Beza sepunya, d=28−16=12Jumlah perimeter, Sn=13.16 m=1316 cmn2[2(16)+(n−1)12]=1316n[32+12n−12]=263212n2+20n−2632=03n2+5n−658=0(n−14)(3n+47)=0n−14=0n=14Atau3n+47=0n=−473 (ditolak)14 buah segi empat sama boleh dibentuk dengan menggunakan dawai 13.16 m.