Bab 8 Bulatan III

Posted on October 16, 2016 by user

8.4.3 SPM Praktis, Bulatan III (Kertas 1)

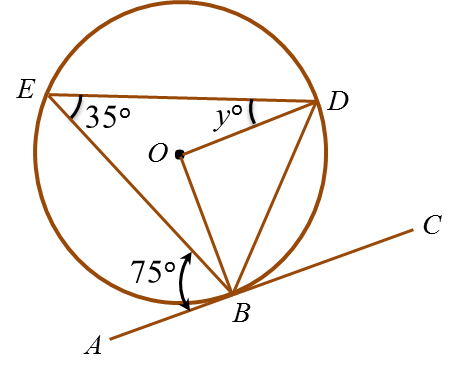
Soalan 9:

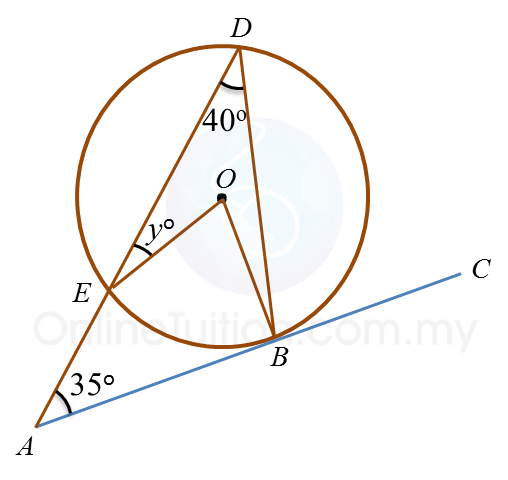
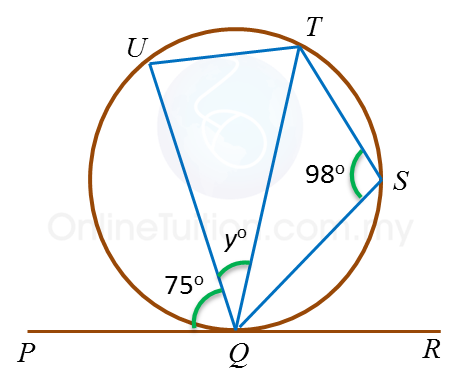
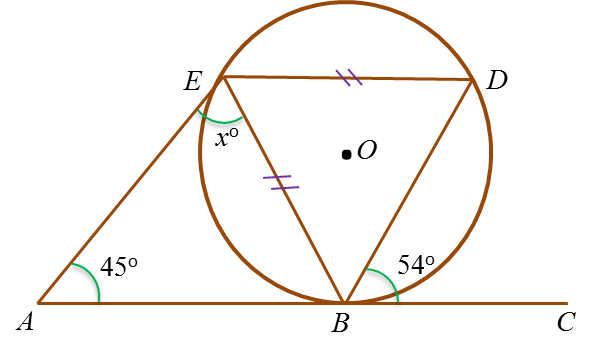
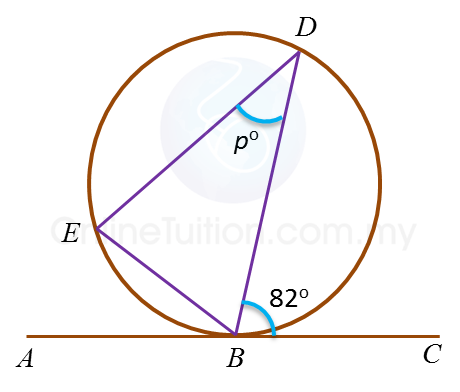
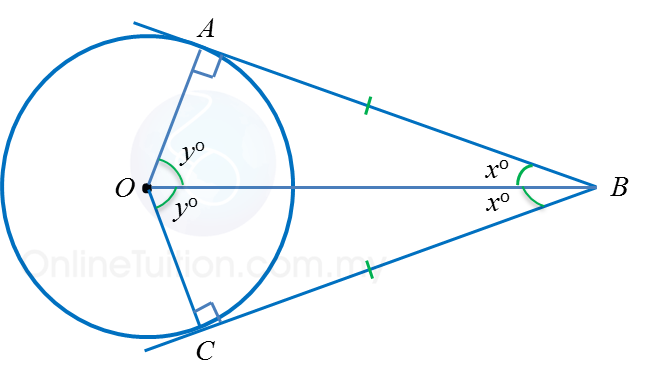
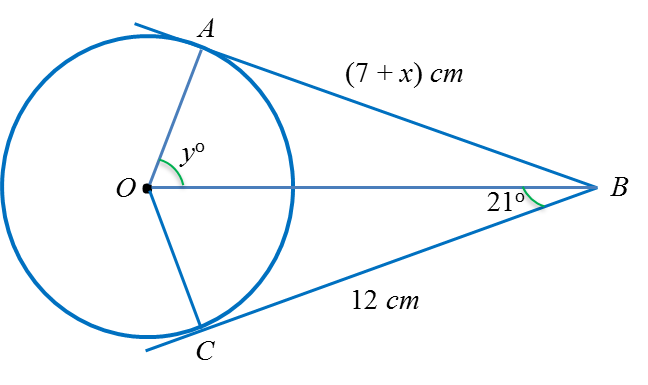
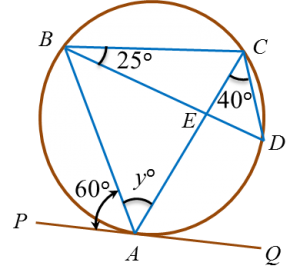
Dalam rajah di atas, ABC ialah tangen kepada bulatan berpusat O , di titik B.

Cari nilai y.

Penyelesaian:

∠ABO = 90^o

∠BOE = 2 × 40^o= 80^o

Dalam segi empat AEOB,

∠AEO = 360^o– ∠ABO– ∠BOE– 35^o

= 360^o– 90^o – 80^o – 35^o= 155^o

y^o+ ∠AEO = 180^o

y^o+ 155^o = 180^o

y^o= 180^o– 155^o

y^o = 25

Soalan 10:

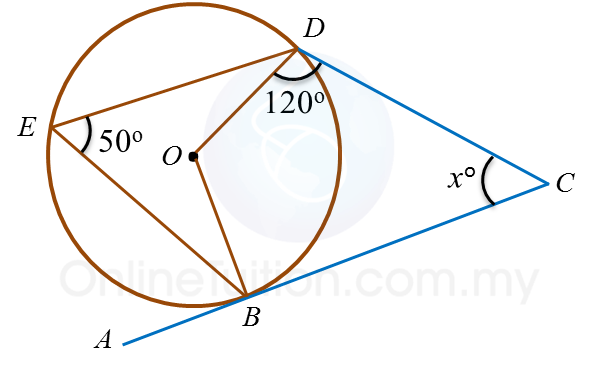
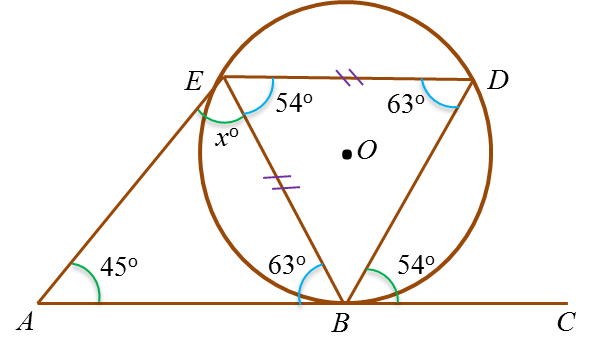
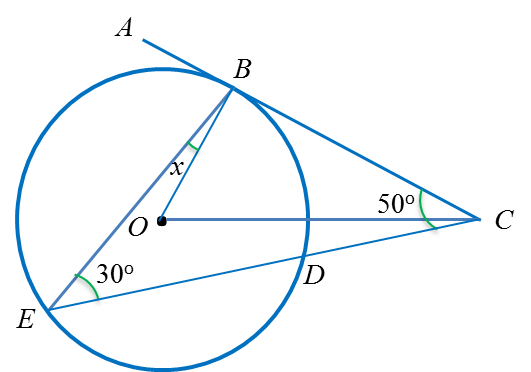
Dalam rajah di atas, ABC ialah tangen kepada bulatan berpusat O, di titik B.

Nilai x ialah

Penyelesaian:

∠OBC = 90^o

∠BOD = 2 × 50^o= 100^o

Dalam segi empat BODC,

x^o= 360^o– ∠BOD – ∠OBC – 120^o

= 360^o– 100^o – 90^o – 120^o

= 50

Bab 8 Bulatan III

Posted on May 4, 2016 by user

8.3 Tangen Sepunya

Tangen sepunya kepada dua bulatan ialah suatu garis lurus yang menyentuh kedua-dua bulatan itu masing-masing pada satu titik sahaja.

1. Bersilang di dua titik
(a) Bulatan sama saiz

Bilangan Tangen Sepunya	Sifat-sifat Tangen Sepunya
Dua tangen sepunya: AB dan CD	AC = BD AB = CD AB selari dengan OR selari dengan CD

(b) Bulatan saiz berbeza

Bilangan Tangen Sepunya	Sifat-sifat Tangen Sepunya
Dua tangen sepunya: ABE dan CDE	AB = CD BE = DE OA // RB OC // RD

2. Bersilang di satu titik
(a) Bulatan sama saiz

Bilangan Tangen Sepunya	Sifat-sifat Tangen Sepunya
Tiga tangen sepunya: AB, CD dan PQ	AC = PQ = BD AB = OR = CD AB // OR // CD AC // PQ // BD PQ berserenjang dengan OR

(b) Bulatan saiz berbeza
(i) Bersentuh di luar bulatan

Bilangan Tangen Sepunya	Sifat-sifat Tangen Sepunya
Tiga tangen sepunya: ABE, CDE dan PQ	AB = CD BE = DE OA // RB OC // RD PQ berserenjang dengan ORE

(ii) Bersentuh di dalam bulatan

Bilangan Tangen Sepunya	Sifat-sifat Tangen Sepunya
Satu tangen sepunya: PQR	ONQ berserenjang dengan PR

3. Tidak bersilang

(a) Bulatan sama saiz

Bilangan Tangen Sepunya	Sifat-sifat Tangen Sepunya
Empat tangen sepunya: AB, CD, PS and RQ	AB = CD = OV PS = RQ AB // OV // CD

(b) Bulatan saiz berbeza

Bilangan Tangen Sepunya	Sifat-sifat Tangen Sepunya
Empat tangen sepunya: AB, CD, PS dan RQ	AB = CD BT = DT PS = RQ OA // VB OC // VD

Bab 8 Bulatan III

Posted on May 4, 2016 by user

8.2.1 Sudut di antara Tangen dengan Perentas (Contoh Soalan)

Contoh 2:

Dalam rajah, PQR ialah tangen kepada bulatan QSTU di titik Q.

Cari nilai bagi y.

Penyelesaian:

∠QUT = 180^o– 98^o ← (sudut bertentangan dalam sisi empat kitaran QSTU)

= 82^o

∠QTU = 75^o ← (sudut dalam tembereng selang-seli)

Oleh itu y = 180^o – (82^o + 75^o) ← (Jumlah sudut dalaman ∆ QTU)

= 23^o

Contoh 3:

Dalam rajah, PQR ialah tangen kepada bulatan QSTU di titik Q.

Cari nilai bagi
(a) x
(b) y

Penyelesaian:

(a)

∠UTS + ∠UQS = 180^o ← (sudut bertentangan dalam sisi empat kitaran QSTU)

105^o + ∠UQS = 180^o

∠UQS = 75^o

x + 75^o + 20^o = 180^o ← (Jumlah sudut garis lurus PQR = 180^o)

x + 95^o = 180^o

x = 85^o

(b)

∠PQU = ∠QSU ← (sudut dalam tembereng selang-seli)

85^o = 35^o + y

y = 50^o

Contoh 4:

Dalam rajah, ABC ialah tangen kepada bulatan BDE dengan pusat O, di titik B.

Cari nilai bagi x.

Penyelesaian:

\begin{array}{l} ∠ B E D = ∠ C B D = 54^{\circ} \\ ∠ B D E \\ = \frac{180^{\circ} - 54^{\circ}}{2} = 63^{\circ} \leftarrow \begin{array}{l} Segi tiga kaki sama \\ ∠ E B D = ∠ E D B \end{array} \end{array}

∠ABE = ∠BDE = 63^o

Dalam ∆ABE,

x^o+ 45^o+ 63^o= 180^o

x^o+ 108^o= 180^o

x = 72

Bab 8 Bulatan III

Posted on May 4, 2016 by user

8.2 Sudut di antara Tangen dengan Perentas

1. Dalam rajah, ABC ialah tangen kepada bulatan di titik B.

2. Perentas PB membahagikan bulatan kepada dua tembereng, iaitu tembereng minor PRB dan tembereng major PQB.

3. Sudut dalam tembereng selang-seli yang dicangkum oleh perentas PB yang melalui titik sentuhan tangen ialah ∠BQP.

4. Manakala, sudut dalam tembereng selang-seli yang dicangkum oleh perentas BQ yang melalui titik sentuhan tangen ialah ∠BPQ.

5. Sudut di antara tangen dengan perentas yang melalui titik sentuhan tangen adalah sama dengan sudut dalam tembereng selang-seli yang dicangkum oleh perentas itu.

6. Hubungan antara sudut-sudut adalah berikut:

∠ ABP = ∠ BQP

∠ CBQ = ∠ BPQ

Contoh 1:

Dalam rajah di atas, ABC ialah tangen kepada bulatan BDE di titik B.

Panjang lengkok BD adalah sama dengan panjang lengkok DE.

Cari nilai bagi p.

Penyelesaian:

∠BED = 82^o ← (sudut dalam tembereng selang-seli)

∠DBE = 82^o ← (Lengkok BD = Lengkok DE, BDE ialah segi tiga kaki sama)

Oleh itu p= 180^o – 82^o – 82^o

= 16^o

Bab 8 Bulatan III

Posted on May 3, 2016 by user

8.1 Tangen kepada Bulatan

1. Tangen kepada bulatan ialah garis lurus yang menyentuh bulatan itu pada satu titik sahaja. Titik tersebut dipanggil titik sentuhan.

2. Jejari yang melalui titik sentuhan tangen adalah berserenjang dengan tangen itu.

Jika ABC ialah tangen kepada bulatan di B, maka ∠ABO = ∠CBO = 90^o.

8.1.1 Sifat-sifat Berkaitan dengan Dua Tangen kepada Suatu Titik di Luar Bulatan

Dalam rajah di atas, BA dan BC ialah dua tangen dari satu titik luar B. Sifat-sifat bagi tangennya adalah berikut.

\begin{array}{l} (a) B A = B C \\ (b) ∠ A B O = ∠ C B O = x^{o} \\ (c) ∠ A O B = ∠ C O B = y^{o} \\ (d) ∠ O A B = ∠ O C B = 90^{o} \\ (e) ∠ A O C + ∠ A B C = 180^{o} \\ (f) Δ A O B dan Δ C O B adalah kongruen \end{array}

Contoh 1:

Rajah di atas menunjukkan sebuah bulatan dengan pusat O. ABC dan CDE ialah dua tangen kepada bulatan di titik B dan D masing-masing. Cari panjang OC

Penyelesaian:

OC²= OB² + BC² ← (Teori Pythagoras)

= 6²+ 8²

= 100

OC = √100 = 10 cm

Contoh 2:

Dalam rajah di atas, AB dan BC ialah dua tangen kepada bulatan dengan pusat O. Hitung nilai bagi
(a) x (b) y

Penyelesaian:

(a) AB = BC

7 + x = 12

x = 5

(b)

∠OBA = ∠OCB = 21^o

∠OCB = 90^o← (OC berserenjang dengan CB)

y^o= 180^o– 21^o– 90^o

y = 69

Contoh 3:

Dalam rajah di atas, ABC ialah tangen kepada bulatan dengan pusat O di titikt B. CDE ialah garis lurus. Cari nilai bagi x.

Penyelesaian:

∠CBO = 90^o← (OB berserenjang dengan BC)

Dalam ∆ BCE,

x^o= 180^o– 30^o– 50^o – 90^o

x = 10^o

Bab 8 Bulatan III

Posted on April 30, 2016 by user

8.3.1 Tangen Sepunya (Contoh Soalan)

Contoh 1:

Dalam rajah di atas, O dan F ialah pusat bagi dua bulatan yang bersilang. ABG dan CDG ialah tangen-tangen sepunya kepada bulatan-bulatan itu. Cari nilai
(a) x, (b) y, (c) z

Penyelesaian:

(a)

Dalam ∆ BFG,

∠BFG = ½× 56^o = 28^o

∠FBG= 90^o ← (jejari berserenjang dengan tangen)

x^o+ 28^o + 90^o = 180^o

x^o= 180^o – 118^o

x^o= 62^o

x = 62

(b)

∠AOF= x^o = 62^o ← (AO // BF)

y^o= 2 × 62^o

y^o= 124^o

y = 124

(c)

Sudut luaran bagi AOC = 360^o – 124^o = 236^o

∠EOC = ½ × 236^o = 118^o

z^o= (180^o – 118^o) × ½ ← (∆ EOC ialah segitiga kaki sama, ∠OEC = ∠OCE)

z^o= 31^o

z = 31

Bab 8 Bulatan III

Posted on April 30, 2016 by user

Soalan 5:

Dalam rajah di atas, PAQ ialah tangen kepada bulatan ABCD di titik A. AEC dan BED ialah garis lurus. Nilai bagi y ialah

Penyelesaian:

∠ABD = ∠ACD = 40^o

∠ACB = ∠PAB = 60^o

y = 180^o– ∠ACB – ∠CBD – ∠ABD

y = 180^o– 60^o – 25^o– 40^o = 55^o

Soalan 6:

Dalam rajah di atas, KPL ialah tangen kepada bulatan PQRS di titik P. Nilai bagi x ialah

Penyelesaian:

∠PQS = ∠SPL= 55^o

∠SPQ = 180^o– 30^o – 55^o= 95^o

Dalam sisi empat kitaran,

∠SPQ + ∠SRQ = 180^o

95^o+ x^o = 180^o

x = 85^o

Soalan 7:

Dalam rajah di atas, APB ialah tangen kepada bulatan PQR di titik P. QRB ialah garis lurus.
Nilai bagi x ialah

Penyelesaian:

∠PQR = ∠RPB= 45^o

∠QPR = (180^o– 45^o) ÷ 2 = 67.5^o

∠PQR + ∠BPQ + x^o = 180^o

45^o+ (67.5^o + 45^o) + x^o = 180^o

x = 22.5^o

Soalan 8:

Rajah di atas menunjukkan dua bulatan berpusat di O dan V. AB ialah tangen sepunya kepada bulatan-bulatan itu. OPRV ialah garis lurus. Panjang PR, dalam cm, ialah

Penyelesaian: