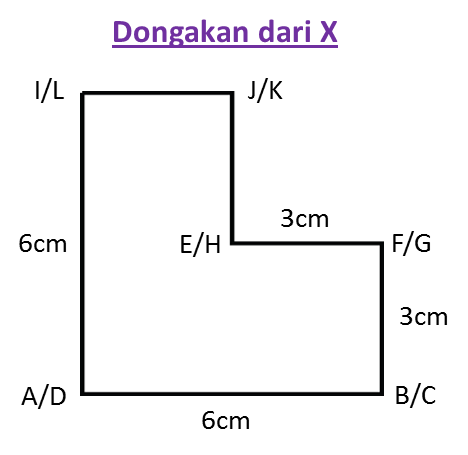
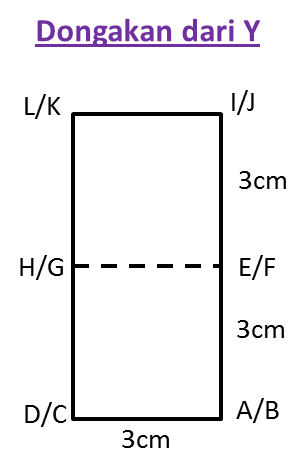
Soalan 3:
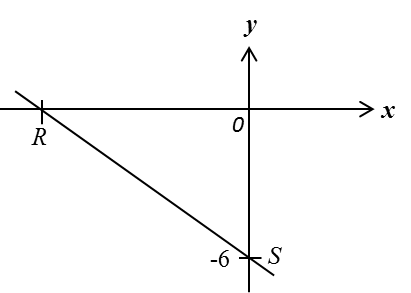
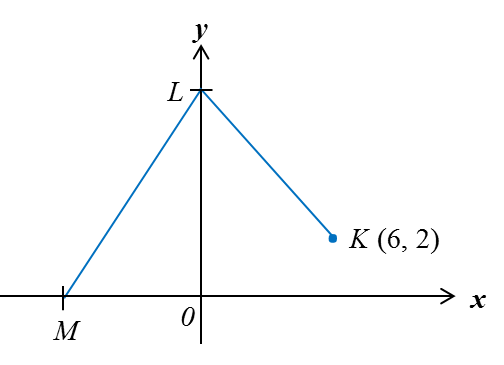
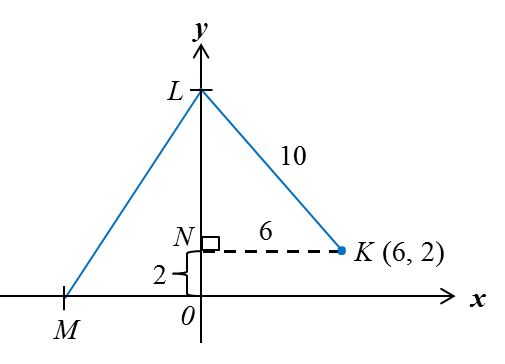
(a) Rajah di bawah menunjukkan dua titik, M dan N, pada suatu satah Cartesan.
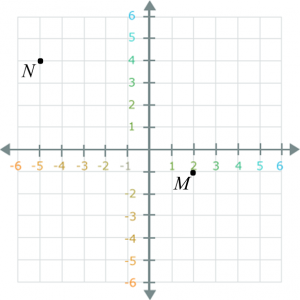
Penjelmaan T ialah satu translasi dan penjelmaan R ialah satu putaran 90o lawan arah jam pada pusat (0, 2).
(i) Nyatakan koordinat imej bagi titik M di bawah penjelmaan R.
(ii) Nyatakan koordinat imej bagi titik N di bawah penjelmaan berikut:
(a) T2,
(b) TR,
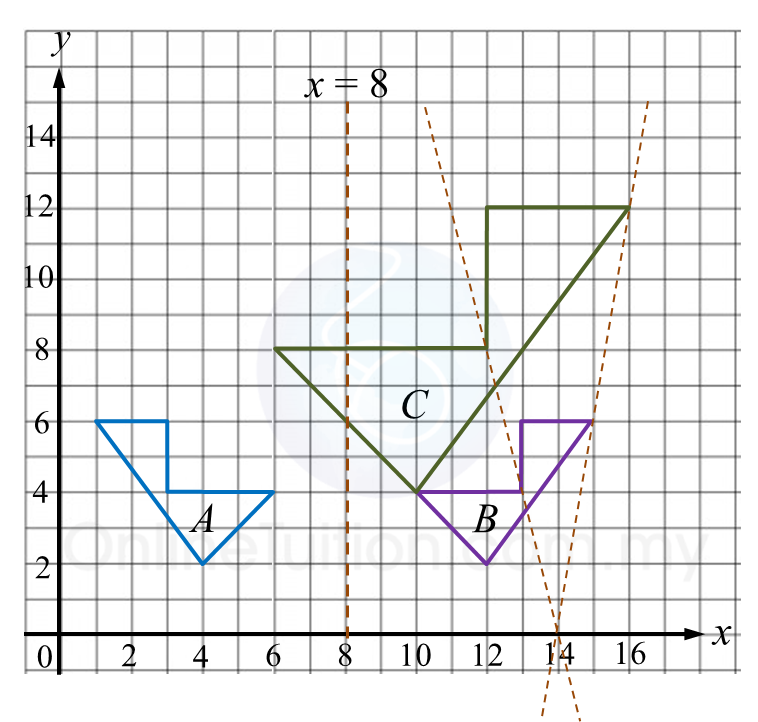
(b) Rajah di bawah menunjukkan tiga pentagon, A, B dan C, dilukis pada suatu satah Cartesan.

(i) C ialah imej bagi A di bawah gabungan penjelmaan WV.
Huraikan selengkapnya penjelmaan:
(a) V (b) W
(ii) Diberi bahawa A mewakili suatu kawasan yang mempunyai luas 12 m2, hitung luas, dalam m2, kawasan yang diwakili oleh C.
Penyelesaian:
(a)
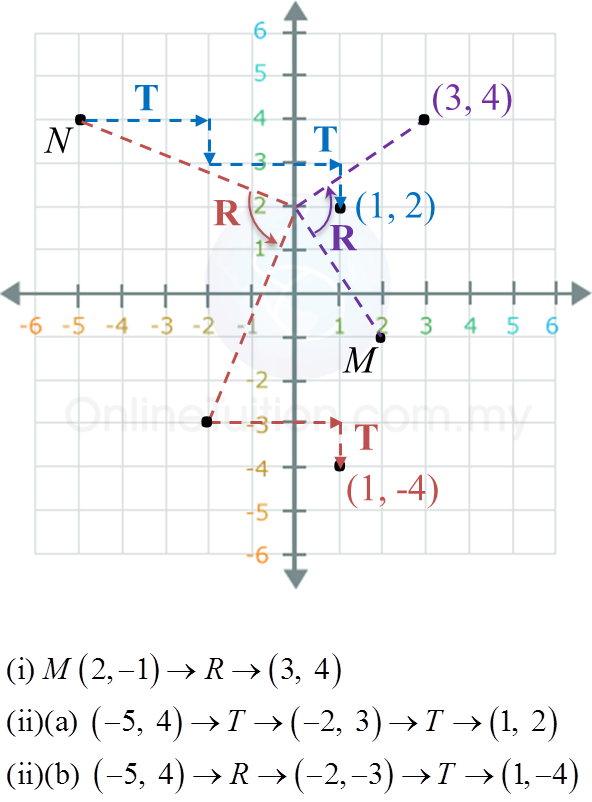
(b)
(b)(i)(a)
V: Satu pantulan pada garis x = 8
(b)(i)(b)
W: Satu pembesaran pada pusat (14, 0) dengan faktor skala.
(b)(ii)
Luas B = luas A = 12 m2
Luas C = (faktor skala)2 x Luas objek
= 22 x luas B
= 22 x 12
= 48 m2
(a) Rajah di bawah menunjukkan dua titik, M dan N, pada suatu satah Cartesan.

Penjelmaan T ialah satu translasi dan penjelmaan R ialah satu putaran 90o lawan arah jam pada pusat (0, 2).
(i) Nyatakan koordinat imej bagi titik M di bawah penjelmaan R.
(ii) Nyatakan koordinat imej bagi titik N di bawah penjelmaan berikut:
(a) T2,
(b) TR,
(b) Rajah di bawah menunjukkan tiga pentagon, A, B dan C, dilukis pada suatu satah Cartesan.

(i) C ialah imej bagi A di bawah gabungan penjelmaan WV.
Huraikan selengkapnya penjelmaan:
(a) V (b) W
(ii) Diberi bahawa A mewakili suatu kawasan yang mempunyai luas 12 m2, hitung luas, dalam m2, kawasan yang diwakili oleh C.
Penyelesaian:
(a)

(b)

(b)(i)(a)
V: Satu pantulan pada garis x = 8
(b)(i)(b)
W: Satu pembesaran pada pusat (14, 0) dengan faktor skala.
(b)(ii)
Luas B = luas A = 12 m2
Luas C = (faktor skala)2 x Luas objek
= 22 x luas B
= 22 x 12
= 48 m2
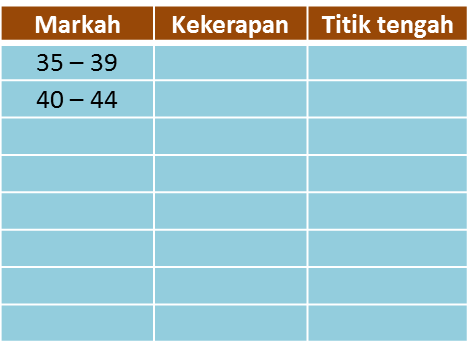
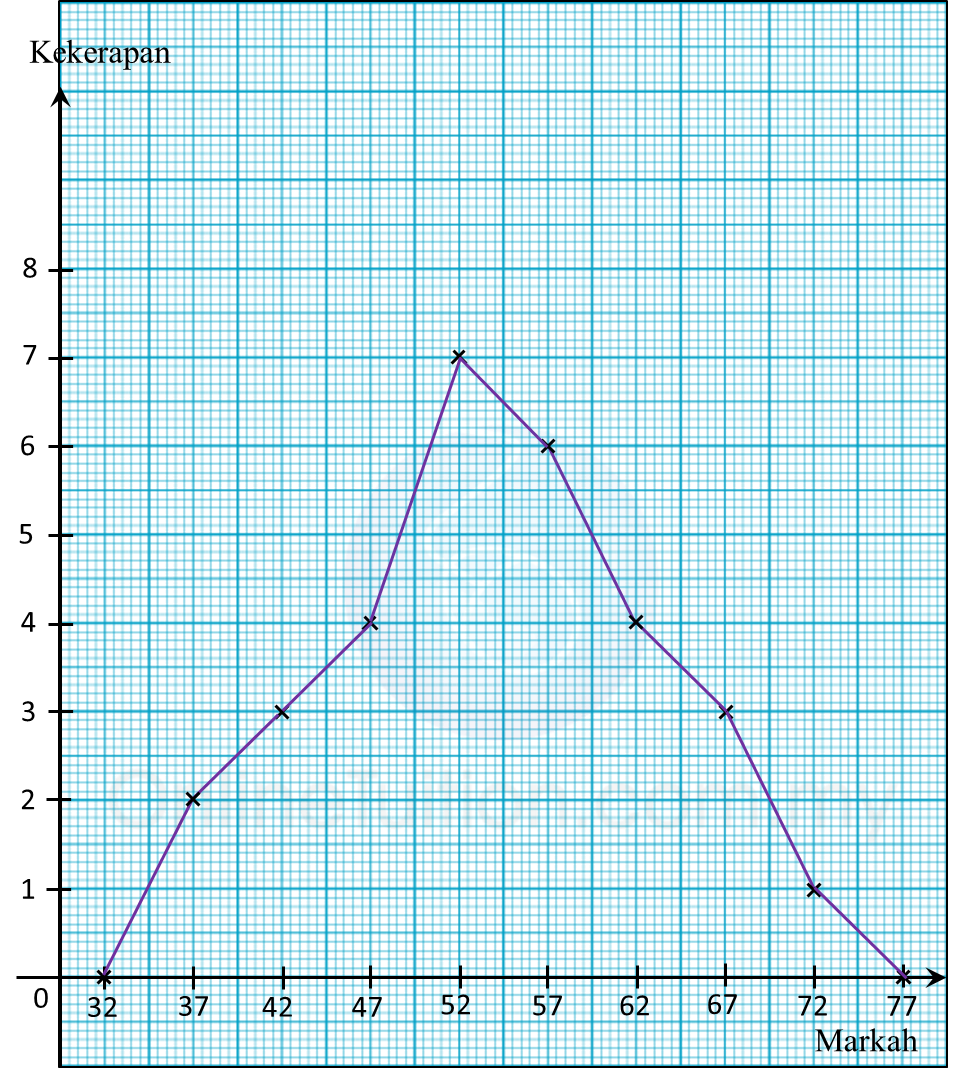
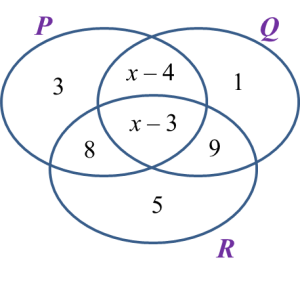
 (a) Berdasarkan data dalam rajah di atas, lengkapkan Jadual di ruang jawapan.
(a) Berdasarkan data dalam rajah di atas, lengkapkan Jadual di ruang jawapan.