10.3.1 Pelan dan Dongakan, SPM Praktis (Kertas 2)
Soalan 1:
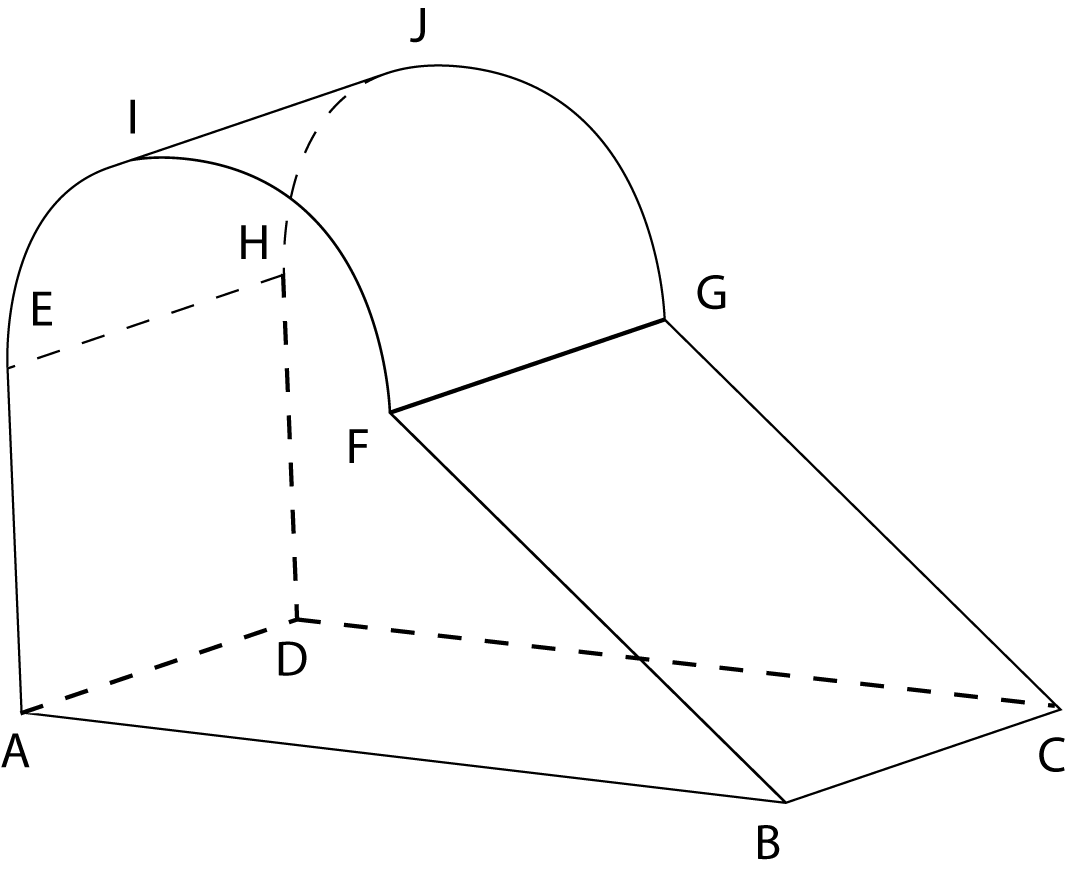
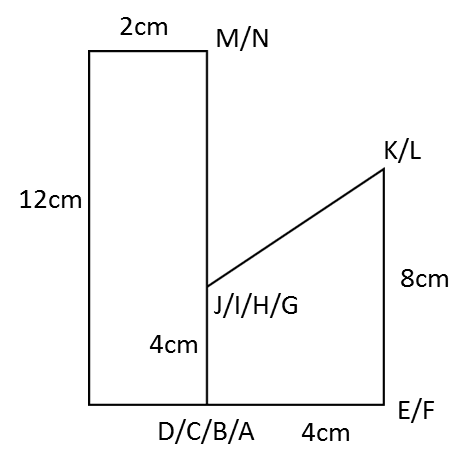
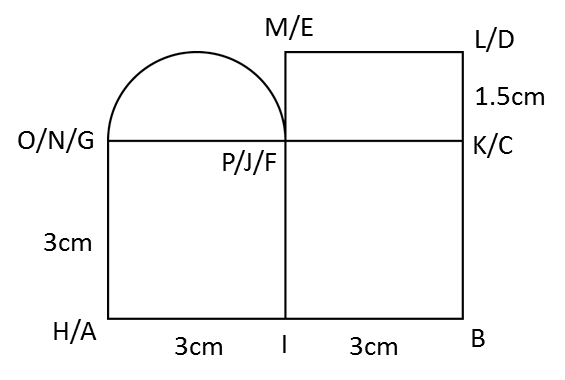
Rajah di atas menunjukkan sebuah pepejal yang terdiri daripada sebuah prisma tegak dan sebuah separuh silinder yang dicantumkan pada satah EFGH. EF ialah diameter kepada separuh silinder dan berukuran 3cm. Tapak ABCD terletak di atas satu satah mengufuk dan AB = 6cm, BC = 4cm. Satah mencancang ABFE ialah keratan rentas seragam prisma itu.
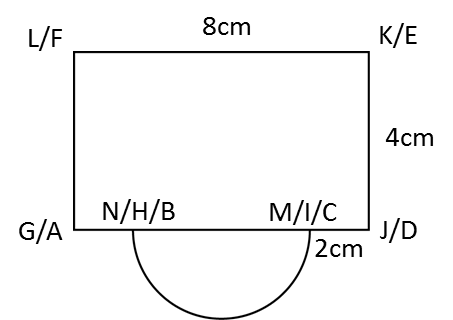
Lukis dengan skala penuh, Plan pepejal itu.
Lukis dengan skala penuh, Plan pepejal itu.
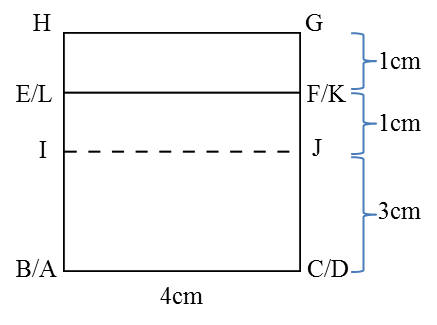
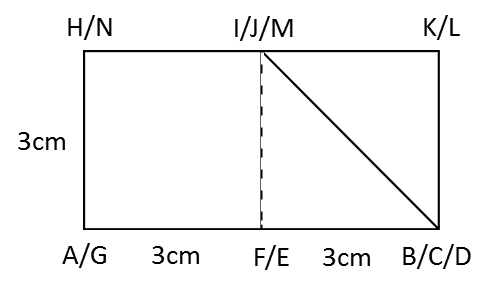
Penyelesaian:


Soalan 2:
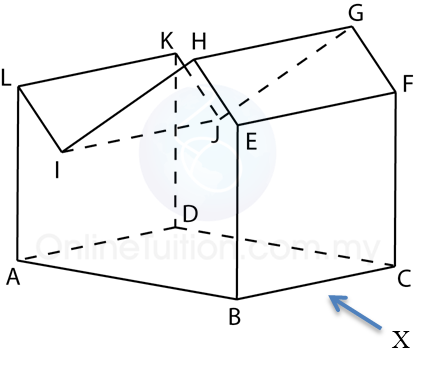
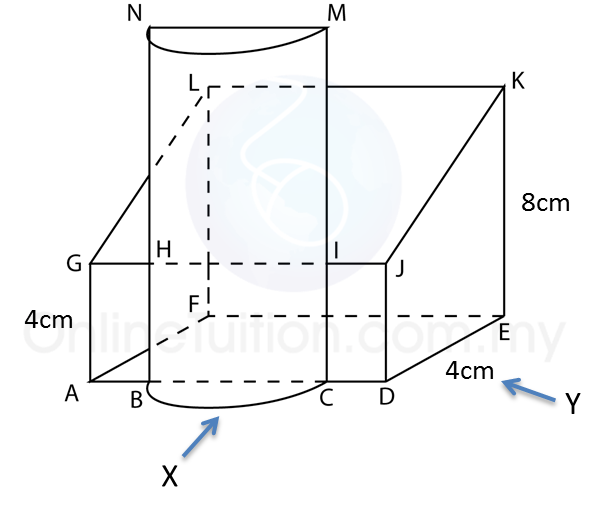
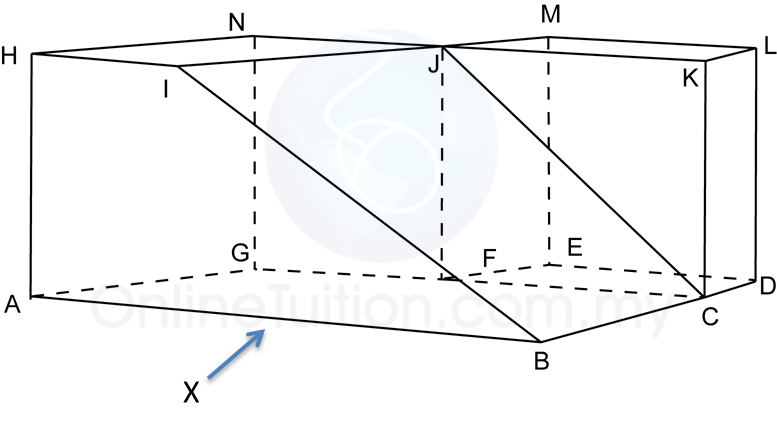
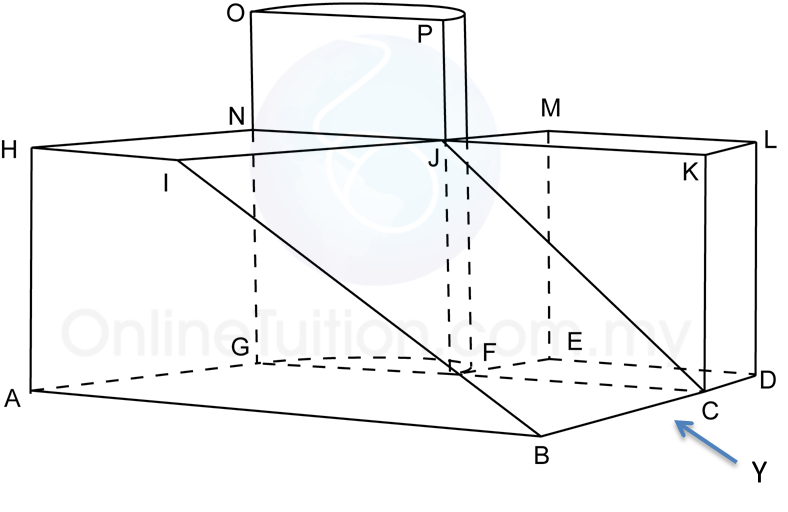
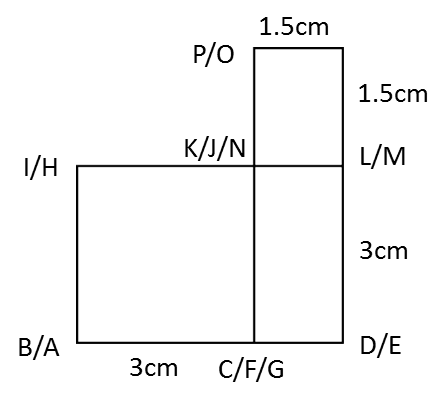
Rajah di atas menunjukkan sebuah pepejal berbentuk prisma tegak dengan tapak segi empat tepat ABCD atas sebuah meja mengufuk. Satah mencancang ABEHIL ialah keratan rentas seragam prisma itu. Segi empat tepat LIJK, IHGJ dan HEFG adalah satah condong. Tepi AL, DK, BE dan CF adalah tegak.
Diberi BC = 4cm, AB = 6cm. EB = FC = LA = KD = 4cm, dan tinggi mencancang bagi I dan J dari tapak segi empat tepat ABCD = 3cm, manakala tinggi mencancang bagi H dan G dari tapak segi empat tepat ABCD = 5cm.
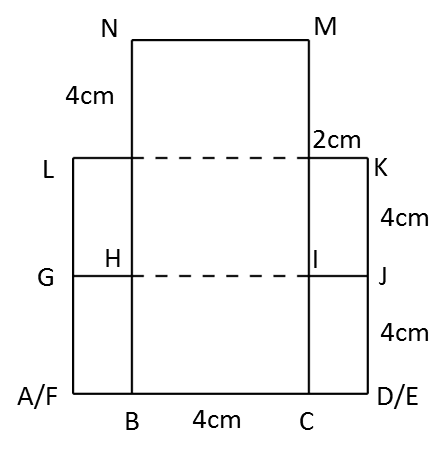
Lukis dengan skala penuh, dongakan pepejal itu pada satah mencancang yang selari dengan BC sebagaimana dilihat dari X.
Lukis dengan skala penuh, dongakan pepejal itu pada satah mencancang yang selari dengan BC sebagaimana dilihat dari X.
Penyelesaian: