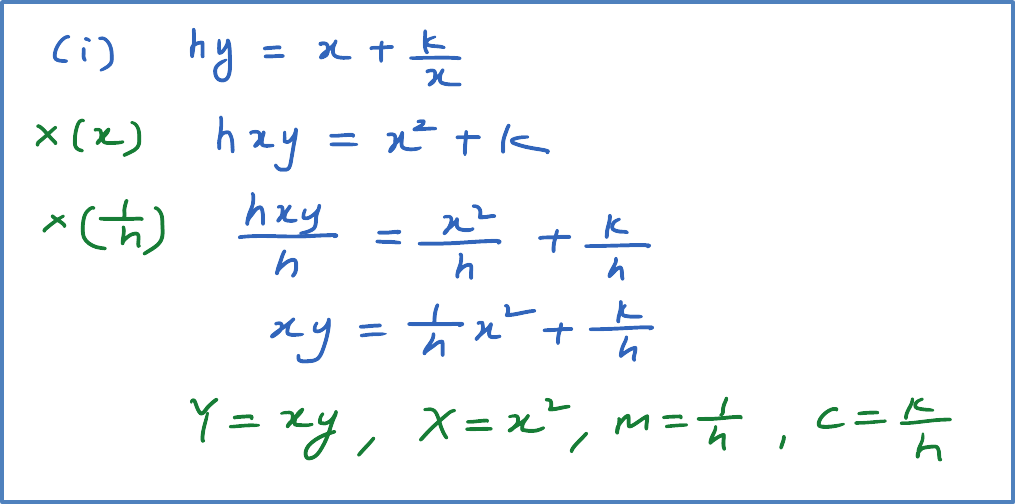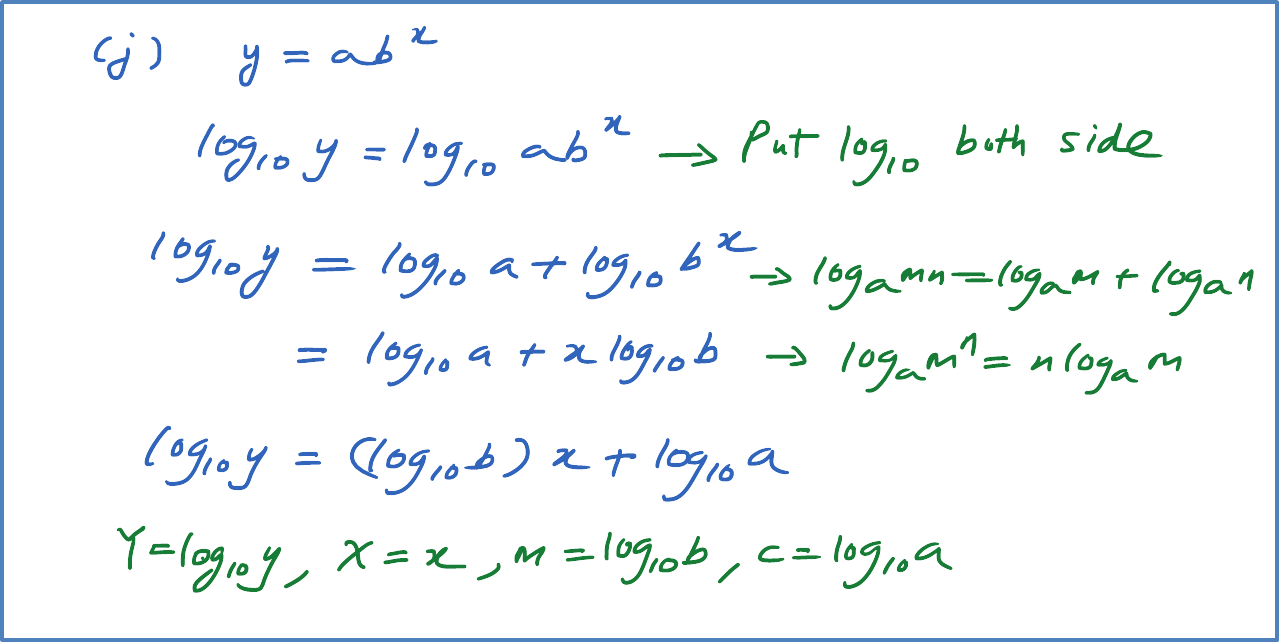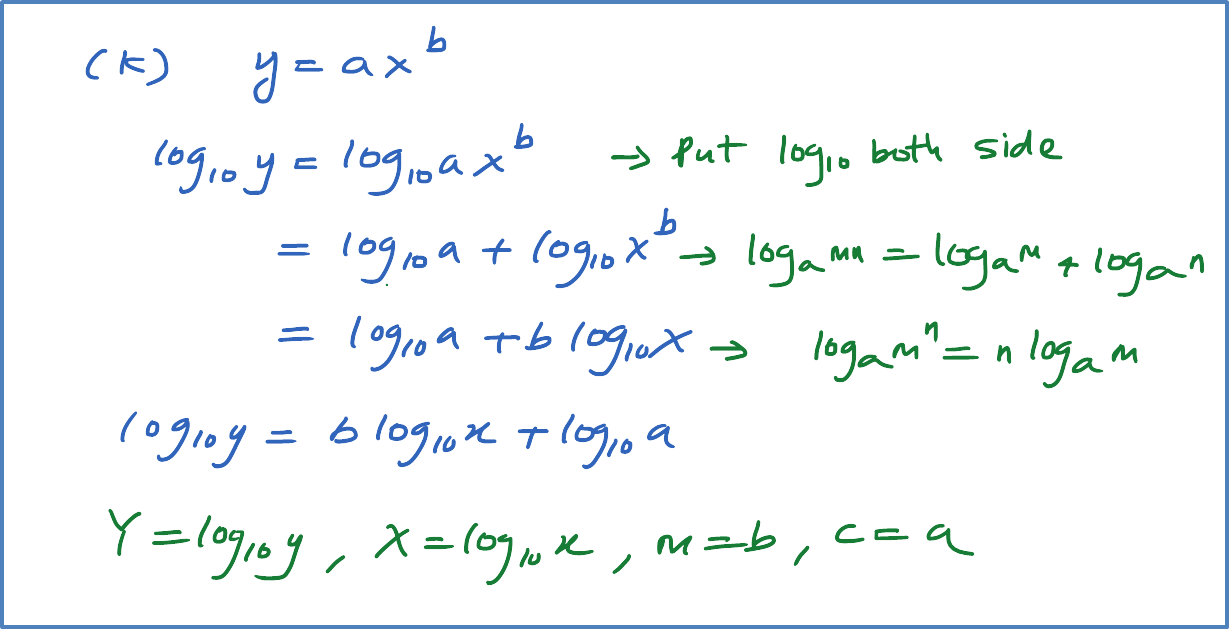Definite Integrals

Posted on April 22, 2020 by user

3.4a Definite Integral of f(x) from x=a to x=b

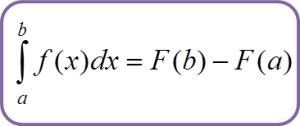
Example:

Evaluate each of the following.

\begin{array}{l} (a) \int_{- 1}^{0} (3 x^{2} - 2 x + 5) d x \\ (b) \int_{0}^{2} {(2 x + 1)}^{3} d x \end{array}

Solution:

\begin{array}{l} (a) \int_{- 1}^{0} (3 x^{2} - 2 x + 5) d x \\ = {[\frac{3 x^{3}}{3} - \frac{2 x^{2}}{2} + 5 x]}_{- 1}^{0} \\ = {[x^{3} - x^{2} + 5 x]}_{- 1}^{0} \\ = 0 - [{(- 1)}^{3} - {(- 1)}^{2} + 5 (- 1)] \\ = 0 - (- 1 - 1 - 5) \\ = 7 \\ (b) \int_{0}^{2} {(2 x + 1)}^{3} d x \\ = {[\frac{{(2 x + 1)}^{4}}{4 (2)}]}_{0}^{2} \\ = {[\frac{{(2 x + 1)}^{4}}{8}]}_{0}^{2} \\ = [\frac{{(2 (2) + 1)}^{4}}{8}] - [\frac{{(2 (0) + 1)}^{4}}{8}] \\ = \frac{625}{8} - \frac{1}{8} \\ = 78 \end{array}

Short Question 2 – 4

Posted on April 22, 2020 by user

Question 2:

Given that

Given that \int \frac{4}{{(1 + x)}^{4}} d x = m {(1 + x)}^{n} + c,

find the values of m and n.

Solution:

\begin{array}{l} \int \frac{4}{{(1 + x)}^{4}} d x = m {(1 + x)}^{n} + c \\ \int 4 {(1 + x)}^{- 4} d x = m {(1 + x)}^{n} + c \\ \frac{4 {(1 + x)}^{- 3}}{- 3 (1)} + c = m {(1 + x)}^{n} + c \\ - \frac{4}{3} {(1 + x)}^{- 3} + c = m {(1 + x)}^{n} + c \\ m = - \frac{4}{3}, n = - 3 \end{array}

Question 3:

\begin{array}{l} Given \int_{- 1}^{2} 2 g (x) d x = 4, and \int_{- 1}^{2} [m x + 3 g (x)] d x = 15. \\ Find the value of constant m . \end{array}

Solution:

\begin{array}{l} \int_{- 1}^{2} [m x + 3 g (x)] d x = 15 \\ \int_{- 1}^{2} m x d x + \int_{- 1}^{2} 3 g (x) d x = 15 \\ {[\frac{m x^{2}}{2}]}_{- 1}^{2} + 3 \int_{- 1}^{2} g (x) d x = 15 \\ [\frac{m {(2)}^{2}}{2} - \frac{m {(- 1)}^{2}}{2}] + \frac{3}{2} \int_{- 1}^{2} 2 g (x) d x = 15 \\ 2 m - \frac{1}{2} m + \frac{3}{2} (4) = 15 \leftarrow given \int_{- 1}^{2} 2 g (x) d x = 4 \\ \frac{3}{2} m + 6 = 15 \\ \frac{3}{2} m = 9 \\ m = 9 \times \frac{2}{3} \\ m = 6 \end{array}

Question 4:

Given \frac{d}{d x} (\frac{2 x}{3 - x}) = g (x), find \int_{1}^{2} g (x) d x .

Solution:

\begin{array}{l} Given \frac{d}{d x} (\frac{2 x}{3 - x}) = g (x) \\ \int g (x) d x = \frac{2 x}{3 - x} \\ Thus, \\ \int_{1}^{2} g (x) d x = {[\frac{2 x}{3 - x}]}_{1}^{2} \\ = \frac{2 (2)}{3 - 2} - \frac{2 (1)}{3 - 1} \\ = 4 - 1 \\ = 3 \end{array}

Long Question 6

Posted on April 22, 2020 by user

Question 6:
Diagram below shows part of the curve

y = \frac{2}{{(3 x - 2)}^{2}}

which passes through B (1, 2).

(a) Find the equation of the tangent to the curve at the point B.
(b) A region is bounded by the curve, the x-axis and the straight lines x = 2 and x = 3.
(i) Find the area of the region.
(ii) The region is revolved through 360° about the x–axis. Find the volume generated, in terms of p.

Solution:
(a)

\begin{array}{l} y = \frac{2}{{(3 x - 2)}^{2}} = 2 {(3 x - 2)}^{- 2} \\ \frac{d y}{d x} = - 4 {(3 x - 2)}^{- 3} (3) \\ \frac{d y}{d x} = \frac{- 12}{{(3 x - 2)}^{3}} \\ \frac{d y}{d x} = \frac{- 12}{{(3 (1) - 2)}^{3}}, x = 1 \\ \frac{d y}{d x} = - 12 \\ y - 2 = - 12 (x - 1) \\ y - 2 = - 12 x + 12 \\ y = - 12 x + 14 \end{array}

(b)(i)

\begin{array}{l} Area = \int_{2}^{3} y d x \\ = \int_{2}^{3} \frac{2}{{(3 x - 2)}^{2}} d x = \int_{2}^{3} 2 {(3 x - 2)}^{- 2} d x \\ = {[\frac{2 {(3 x - 2)}^{- 1}}{- 1 (3)}]}_{2}^{3} \\ = {[- \frac{2}{3 (3 x - 2)}]}_{2}^{3} \\ = [- \frac{2}{3 [3 (3) - 2]}] - [- \frac{2}{3 [3 (2) - 2]}] \\ = - \frac{2}{21} + \frac{1}{6} \\ = \frac{1}{14} {unit}^{2} \end{array}

(b)(ii)

\begin{array}{l} Volume generated \\ = π \int y^{2} d x \\ = π \int_{2}^{3} \frac{4}{{(3 x - 2)}^{4}} d x = π \int_{2}^{3} 4 {(3 x - 2)}^{- 4} d x \\ = π {[\frac{4 {(3 x - 2)}^{- 3}}{- 3 (3)}]}_{2}^{3} = π {[- \frac{4}{9 {(3 x - 2)}^{3}}]}_{2}^{3} \\ = π [- \frac{4}{9 {[3 (3) - 2]}^{3}}] - [- \frac{4}{9 {[3 (2) - 2]}^{3}}] \\ = π (- \frac{4}{3087} + \frac{4}{576}) \\ = \frac{31}{5488} π {unit}^{3} \end{array}

3.5 Integration as the Summation of Areas

Posted on April 22, 2020 by user

3.5 Integration as the Summation of Areas

(A) Area of the region between a Curve and the x-axis.

Area of the shaded region;

A = \int_{a}^{b} y d x

(B) Area of the region between a curve and the y-axis.

Area of the shaded region;

A = \int_{a}^{b} x d y

(C) Area of the region between a curve and a straight line.

Area of the shaded region;

A = \int_{a}^{b} f (x) d x - \int_{a}^{b} g (x) d x

SPM Practice 2 (Question 1 – 3)

Posted on April 22, 2020 by user

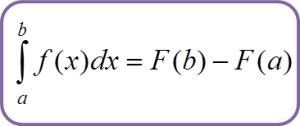
Question 1:
Reduce non-linear relation, $y = p x^{n - 1}$ , where k and n are constants, to linear equation. State the gradient and vertical intercept for the linear equation obtained.
[Note : Reduce No-linear function to linear function]

Solution: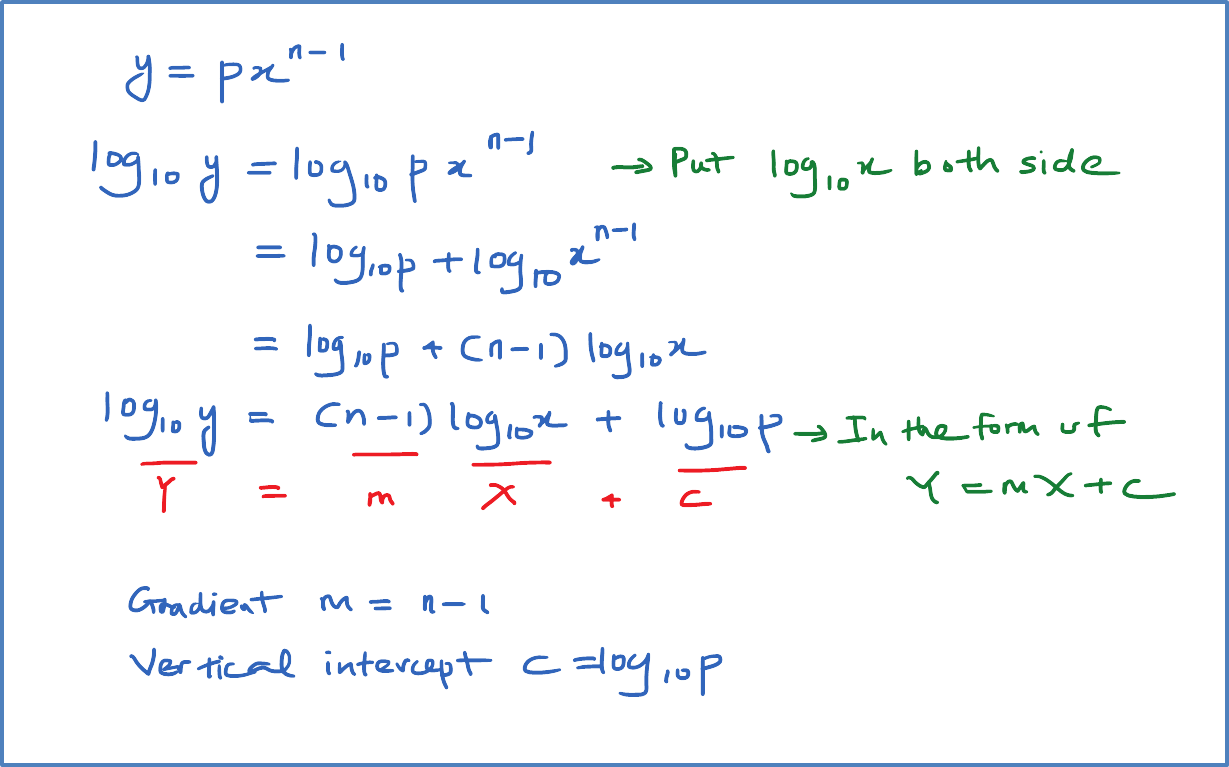

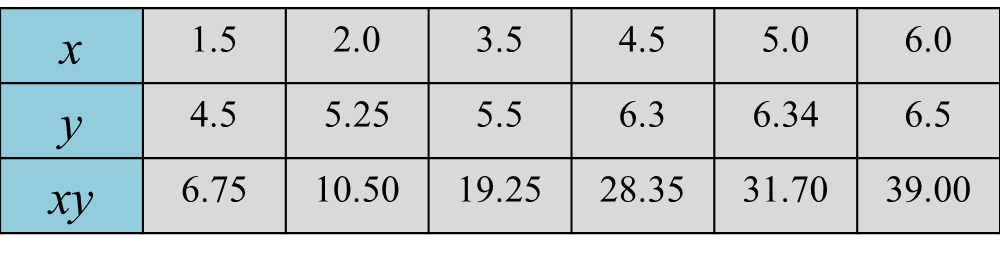
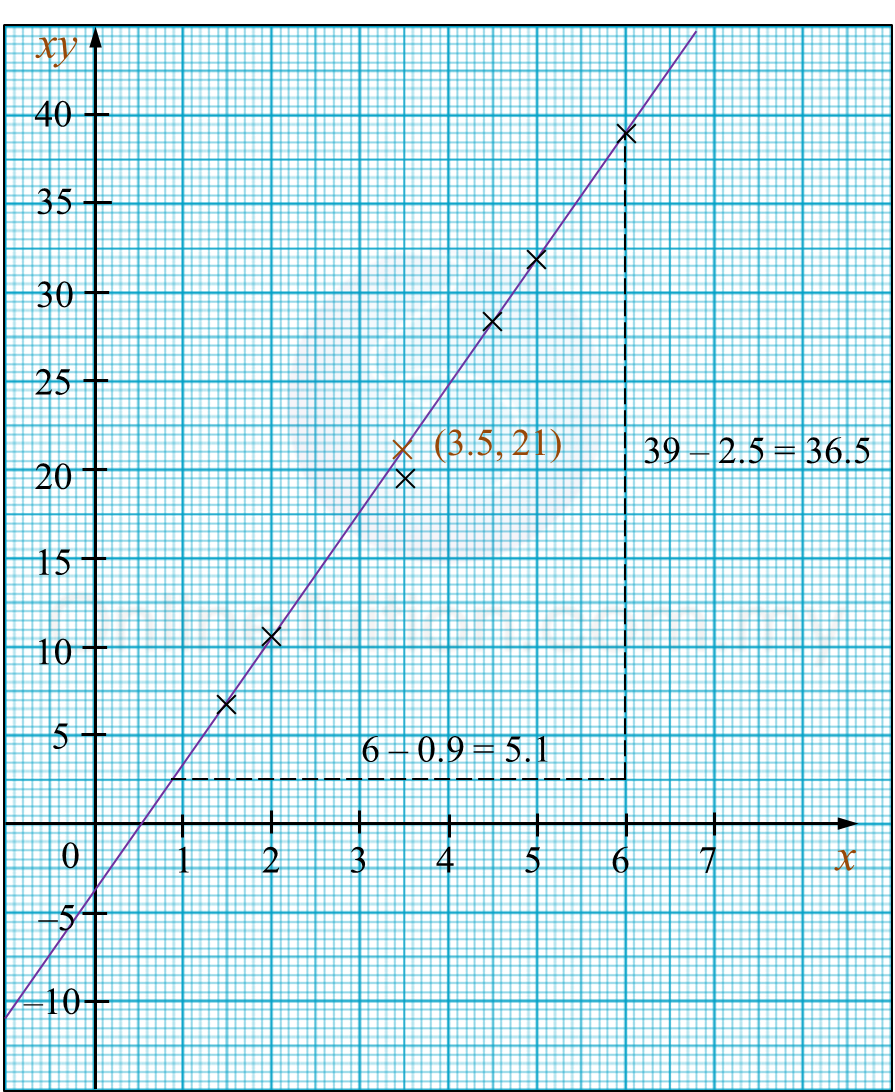
Question 2:
The diagram shows a line of best fit by plotting a graph of 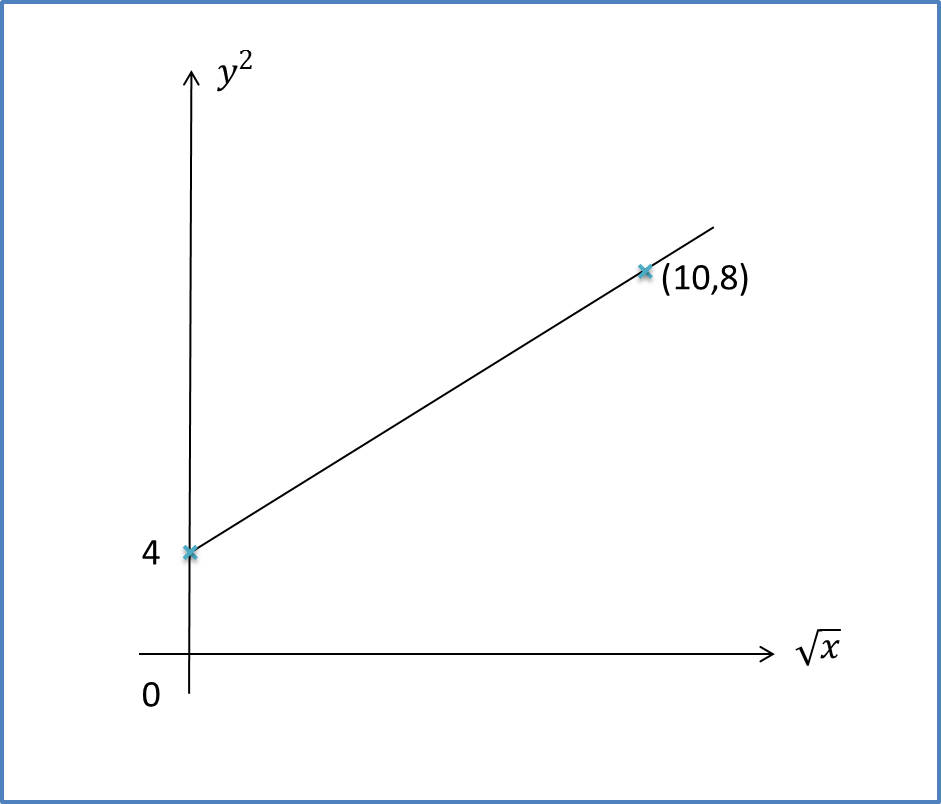$y^{2}$ against $\sqrt{x}$ .

Find the equation of the line of best fit.
Determine the value of
1. x when y = 4,
2. y when x = 25.

Solution:

Question 3:
The diagram shows part of the straight line graph obtained by plotting 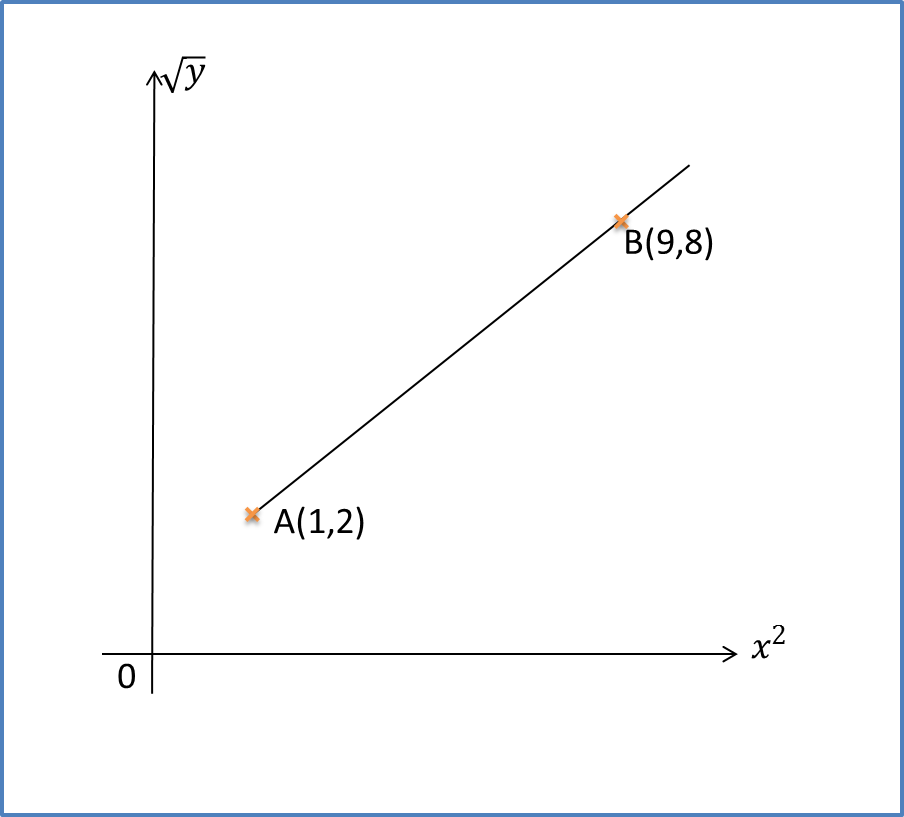$\sqrt{y}$ against $x^{2}$ .

Express y in terms of x.

Solution:

SPM Practice 3 (Linear Law) – Question 1

Posted on April 22, 2020 by user

Question 1 (10 marks):
Use a graph to answer this question.
Table 1 shows the values of two variables, x and y, obtained from an experiment.
The variables x and y are related by the equation

y - \sqrt{h} = \frac{h k}{x}

, where h and k are constants.

(a) Plot xy against x, using a scale of 2 cm to 1 unit on the x-axis and 2 cm to 5 units on the xy-axis.
Hence, draw the line of best fit.

(b) Using the graph in 9(a), find
(i) the value of h and of k,
(ii) the correct value of y if one of the values of y has been wrongly recorded during the experiment.

Solution:
(a)

(b)

\begin{array}{l} y - \sqrt{h} = \frac{h k}{x} \\ x y - \sqrt{h} x = h k \\ x y = \sqrt{h} x + h k \\ Y = m X + C \\ Y = x y, m = \sqrt{h}, C = h k \end{array}

(b)(i)

\begin{array}{l} m = \frac{36.5}{5.1} \\ \sqrt{h} = \frac{36.5}{5.1} \\ \sqrt{h} = 7.157 \\ h = 51.22 \\ C = - 4 \\ h k = - 4 \\ k = \frac{- 4}{h} \\ k = - \frac{4}{51.22} \\ k = - 0.0781 \end{array}

(b)(ii)

\begin{array}{l} x y = 21 \\ 3.5 y = 21 \\ y = \frac{21}{3.5} = 6.0 \\ Correct value of y is 6 .0 . \end{array}

Tips To Reduce Non-Linear Function To Linear Function

Posted on April 22, 2020 by user

Tips:
(1) The equation must have one constant (without x and y).
(2) X and Y cannot have constant, but can have the variables (for example x and y).
(3) m and c can only have the constant (for example a and b), cannot have the variables x and y.

Examples
(1)
X and Y cannot have constant, but can have the variables (for example x and y)

(2)
m and c can only have the constant (for example a and b), cannot have the variables x and y

SPM Practice 2 (Linear Law) – Question 4

Posted on April 22, 2020 by user

Question 4
The table below shows the corresponding values of two variables, x and y, that are related by the equation

y = q x + \frac{p}{q x}

, where p and q are constants.

One of the values of y is incorrectly recorded.
(a) Using scale of 2 cm to 5 units on the both axis, plot the graph of xy against

x^{2}

. Hence, draw the line of best fit

(b) Use your graph in (a) to answer the following questions:
(i) State the values of y which is incorrectly recorded and determine its actual value.
(ii) Find the value of p and of q.

Solution
Step 1 : Construct a table consisting X and Y.

Step 2 : Plot a graph of Y against X, using the scale given and draw a line of best fit

Steps to draw line of best fit - Click here

(b) (i) State the values of y which is incorrectly recorded and determine its actual value.

Step 3 : Calculate the gradient, m, and the Y-intercept, c, from the graph

Step 4 : Rewrite the original equation given and reduce it to linear form

Step 5 : Compare with the values of m and c obtained, find the values of the unknown required

Distance Between Two Points

Posted on April 22, 2020 by user

Distance between point $A (x_{1}, y_{1})$ and point is $B (x_{2}, y_{2})$ given by

$\sqrt{{(x_{1} - x_{2})}^{2} + {(y_{1} - y_{2})}^{2}}$

Reduce Non-Linear Function To Linear Function – Examples (G) To (L)

Posted on April 22, 2020 by user

Examples:
Reduce each of the following equations to the linear form. Hence, state the gradient and the Y-intercept of the linear equations in terms of a and b.

(g)

k x^{2} + t y^{2} = x

(h)

y = \frac{x}{p + q x}

(i)

h y = x + \frac{k}{x}

(j)

y = a b^{x}

(k)

y = a x^{b}

(l)

y = a b^{x + 1}

[Note :
X and Y cannot have constant, but can have the variables (for example x and y)
m and c can only have the constant (for example a and b), cannot have the variables x and y]

Solution: