6.4 Frequency Polygons
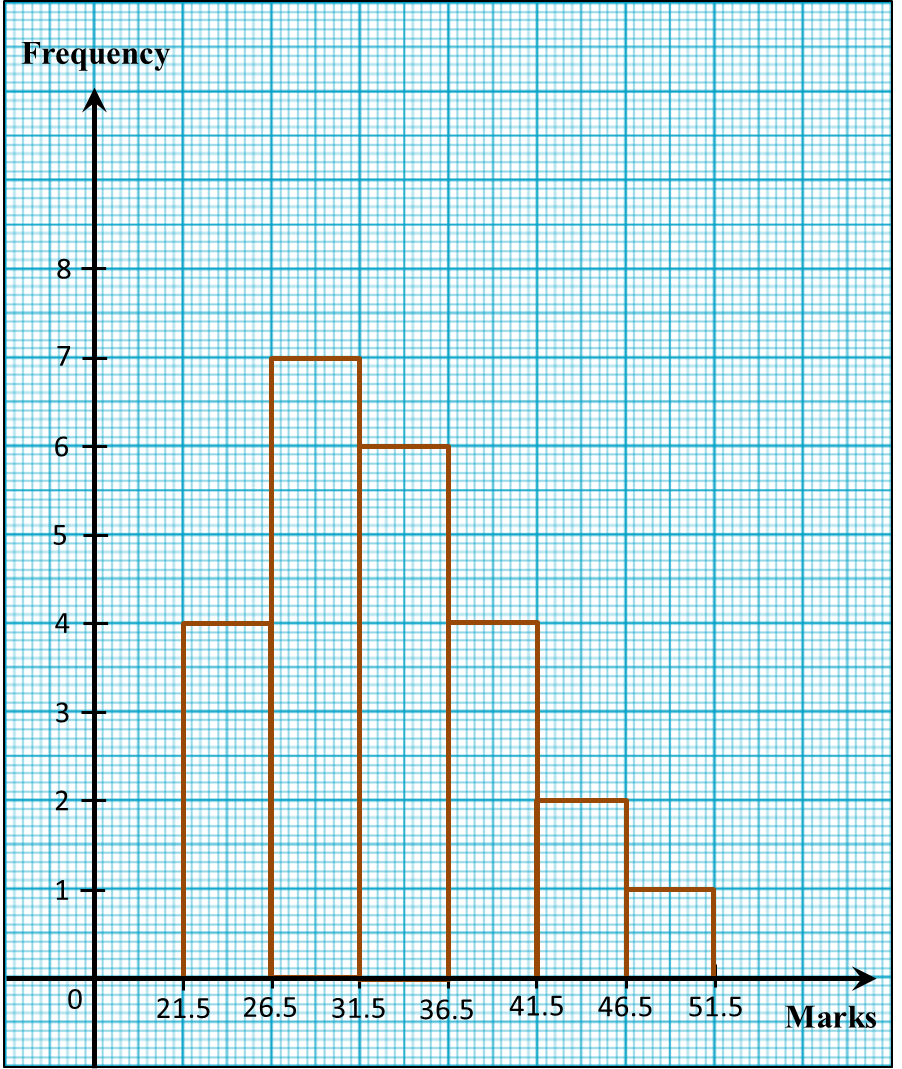
1. A frequency polygon is a line graph that connects the midpoints of each class interval at the top end of each rectangle in a histogram.
2. A frequency polygon can be drawn from a
(a) Histogram,
(b) Frequency table
3. Steps for drawing a frequency polygon:
Step 1: Add a class with 0 frequency before the first class and add also a class with 0 frequency after the last class.
Step 2: Calculate the midpoints or mark the midpoints of the top sides of the rectangular bars including the midpoints of the two additional classes.
Step 3: Joint all the midpoints with straight lines.
Example:
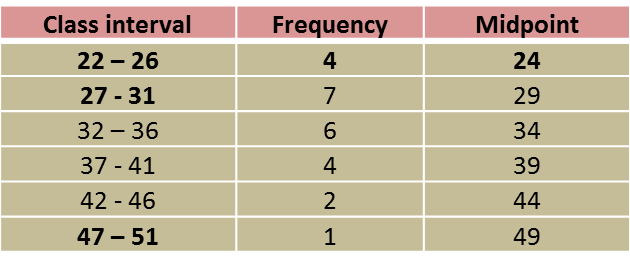
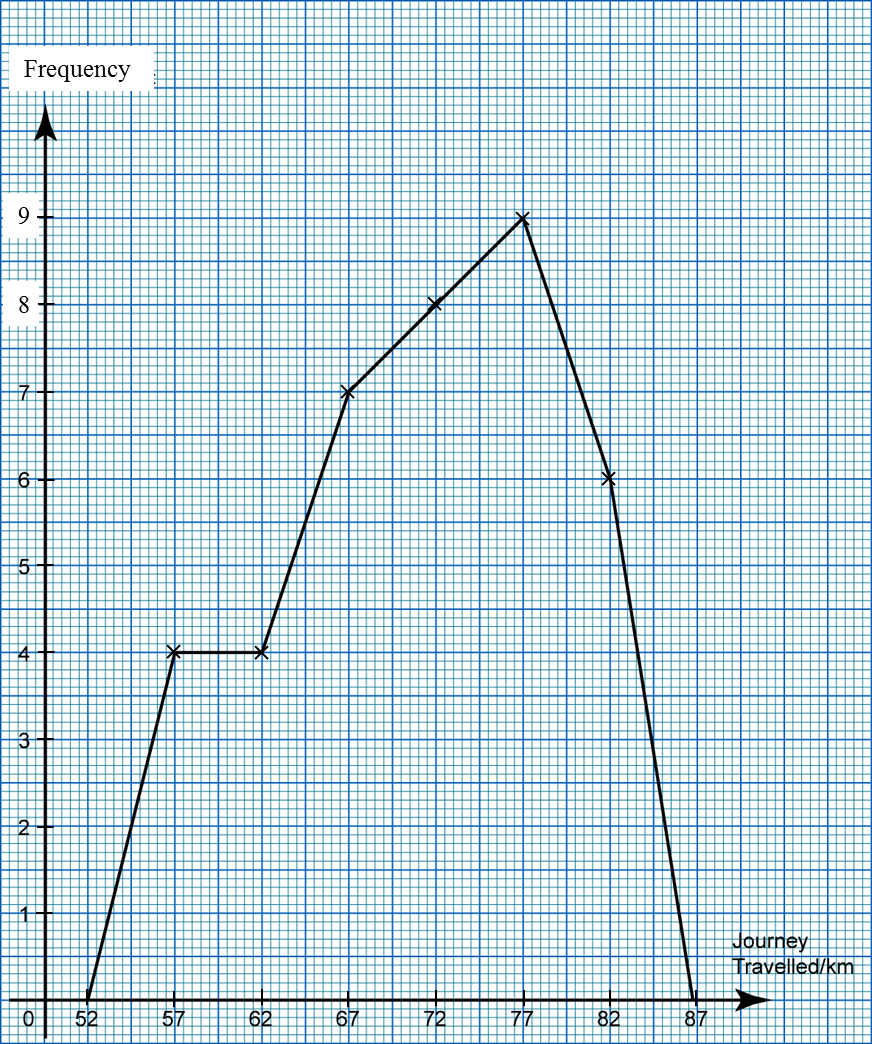
The following frequency table shows the distance travelled by 38 teenagers by motorcycles in one afternoon.
Journey travelled (km) |
Frequency |
55 – 59 |
4 |
60 – 64 |
4 |
65 – 69 |
7 |
70 – 74 |
8 |
75 – 79 |
9 |
80 – 84 |
6 |
Draw a frequency polygon based on the frequency table.
Solution:
Journey travelled (km) |
Frequency |
Midpoint |
50 – 54 |
0 |
52 |
55 – 59 |
4 |
57 |
60 – 64 |
4 |
62 |
65 – 69 |
7 |
67 |
70 – 74 |
8 |
72 |
75 – 79 |
9 |
77 |
80 – 84 |
6 |
82 |
85 – 89 |
0 |
87 |
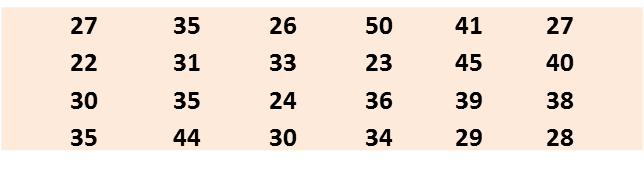 (a) Based on the data in diagram above, complete Table in the answer space.
(a) Based on the data in diagram above, complete Table in the answer space.