4.2 Quantifiers ‘All’ and ‘Some’

Posted on by
4.2 Quantifiers ‘All’ and ‘Some’
 
Statement using ‘All’ and ‘Some’
1. Quantifiers are words that denote the number of objects or cases referred to in a given statement.
2. Quantifier ‘all’, ‘any’ and ‘every’ describe each and every object or case.
3. Quantifier ‘some’, ‘several’ and ‘part of’ describe one or more objects or cases.
 
Example:
Complete each of the following statements using the quantifiers ‘all’ or ‘some’ to make the statement true.
(a) _______  polygons have the same number of vertices and sides.
(b) _______  multiples of 9 are even numbers.
(c) _______  of the whole numbers are divisible by 7.
(d) _______  factors of 4 are factors of 20.
 
Solution:
(a) All polygons have the same number of vertices and sides.
(b) Some multiples of 9 are even numbers.
(c) Some of the whole numbers are divisible by 7.
(d) All factors of 4 are factors of 20.

4.3 Operations on Statements

Posted on by
4.3 Operations on Statements (Part 1)
 
(A) Nagating a Statement using ‘No’ or ‘Not’
 
1. Negation of a statement refers to changing the truth value of the statement, that is, changing a true statement to a false statement and vice versa, using the word ‘not’ or ‘no’.
 
Example 1:
Change the true value of the following statements by using ‘no’ or ‘not’.
(a) 17 is a prime number.
(b) 39 is a multiple of 9.
 
Solution:
(a) 17 is not a prime number. (True to false)
(b) 39 not is a multiple of 9. (False to true)


2. A compound statement can be formed by combining two given statements using the word ‘and’.
 
Example 2:
Identify two statements from each of the following compound statements.
(a) All pentagons have 5 sides and 5 vertices.
(b) 33 = 27 and 43 = 64
 
Solution:
(a) All pentagons have 5 sides.
 All pentagons have 5 vertices.
(b) 33 = 27
  43 = 64



Example 3:
Form a compound statement from each of the following pairs of statements using the word ‘and’.
(a) 19 is a prime number.
  19 is an odd number.
(b) 15 – 5 = 10
  15 × 5 = 75

Solution:
(a) 19 is a prime number and an odd number. ← (Repeated words can be eliminated when combining two statements using ‘and’.)

(b) 15 – 5 = 10 and15 × 5 = 75.


3. A compound statement can also be formed by combining two given statements using the word ‘or’.
 
Example 4:
Form a compound statement from each of the following pairs of statements using the word ‘or’.
(a) 11 is an odd number.
  11 is a prime number.
(b) − 3 = − 27 3 − 3 = − 4 + 1

Solution:
(a) 11 is an odd number or a prime number.
( b) − 3 = − 27 3 or − 3 = − 4 + 1

3.4 SPM Practice (Long Questions)

Posted on by

Question 3:
(a) The Venn diagrams in the answer space shows sets P and Q such that the universal set, ξ = P υ Q.
  Shade the set P ∩ Q.
(b) The Venn diagrams in the answer space shows sets X and Y and Z, such that the universal set, ξ = X υ Y υ Z.
  Shade the set (X υ Z) ∩ Y.

Solution:
(a)

• P ∩ Q means the intersection of the region P and the region Q.

(b)


• (X υ Z) means the union of the region X and the region Z.
• The region then intersects with region Y to give the result (X υ Z) ∩ Y.





Question 4:
The Venn diagrams in the answer space shows sets P, Q and R such that the universal set, ξ = P υ Q υ R
On the diagrams in the answer space, shade
(a) P ∩ R’,
(b) P’υ (Q ∩ R).

Solution:
(a)
P ∩ R’
(b)
P’υ (Q ∩ R)


3.1 Set

Posted on by
3.1 Set
1. A set is a collection of objects according to certain characteristics
2. The objects in a set are known as elements.
3. Sets are usually denoted by capital letters and notation used for sets is braces, {   }.

Example:
A = {1, 3, 5, 7, 9}
 
4. In set notation, the symbol ∈ means ‘is an element of’ or ‘belongs to’ and ∉ means ‘is not an element of’ or ‘does not belong to’.
 
Example 1:
Given that P= {factors of 15} and Q = {positive perfect squares less than 28}. By using the symbol ∈ or ∉ , complete each of the following:
(a) 5 ___  P   (b) 20 ___ P   (c) 25 ___ Q   (d) 8  ___ Q
 
Solution:
P = {1, 3, 5, 15}, Q = {1, 4, 9, 16, 25}

(a) 5 ∈ P ← 5 is an element of set P (b) 20 ∉ P ← 20 is not an element of set P (c) 2 5 ∈ Q ← 2 5 is an element of set Q (d) 8 ∉ Q ← 8 is not an element of set Q



(A) Represent sets by using Venn diagram
5. A set can be represented by a Venn diagram using closed geometry shapes such as circles, rectangles, triangles and etc.

6. A dot to the left of an object in a Venn diagram indicates that the object is an element of the set.

7. When a Venn diagram represents the number of elements in a set, no dot is placed to the left of the number.
 
Example 2:
(a) Draw a Venn diagram to represent each of the following sets.
(b) State the number of elements for each of the set.
A= {2, 3, 5, 7}
B= {k, m, r, t, y}
 
Solution:
(a)
(b)
n(A) = 4
n(B) = 5



(B) Determine whether a set is an empty set
8. A set with no elements is called an empty set or null set. The symbol φ or empty braces, {  }, denotes empty set.
For example, if set A is an empty set, then A = {  } or A = φ and
n (A) = 0.
 
9. If B = {0} or {φ} does not denote that B is an empty set. B = {0} means that there is an element ‘0’ in set B.
B = {φ} means that there is an element ‘φ’ in set B.

3.2 Subset, Universal Set and the Complement of a Set

Posted on by
3.2c Complement of a Set
1. The complement of set B is the set of all elements in the universal set, ξ, which are not elements of set B, and is denoted by B’.

Example 1:
If ξ = {17, 18, 19, 20, 21, 22, 23} and
B = {17, 20, 21} then
B’ = {18, 19, 22, 23}

2. The Venn diagram below shows the relationship between B, B’ and the universal set, ξ.









The complement of set B is represented by the green colour shaded region inside the universal set, ξ, but outside set B.

3.3 Operations on Sets (Part 1)

Posted on by

3.3a Intersection of Sets
 
1. The intersection of set P and set Q, denoted by P ∩ Q  is the set consisting of all elements common to set P and set Q.

2. The intersection of set P, set Q and set R, denoted by P ∩ Q ∩ R  is the set consisting of all elements common to set P, set Q and set R.

3. Represent the intersection of sets using Venn diagrams.

 (a) P ∩ Q





(b) Q ⊂ P , then P ∩ Q = Q

(c) P ∩ Q = ∅ , There is no intersection between set P and set Q .

(d) P ∩ Q ∩ R




3.2 Subset, Universal Set and the Complement of a Set

Posted on by

3.2a Subsets
1. If every element of a set A is also an element of a set B, then set A is called subset of set B.

2. The symbol ⊂ is used to denote ‘is a subset of’.
Therefore, set A is a subset of set B. In set notation, it is written as A ⊂ B.

Example:
A = {11, 12, 13} and B = {10, 11, 12, 13, 14}
Every element of set A is an element of set B.
Therefore  A ⊂ B .

3.   A ⊂ B .  can be illustrated using Venn diagram as below:


4. The symbol   ⊄ is used to denote ‘is not a subset of’.

5. An empty set is a subset of any set.
For example, ∅ ⊂ A

6. A set is a subset of itself.
For example,   B ⊂ B  

7. The number of subsets for a set with n elements is 2n.
For example, if A = {3, 7}
So n = 2, then number of subsets of set A = 22 = 4
All the subsets of set A are { }, {3}, {7} and {3, 7}.

3.2 Subset, Universal Set and the Complement of a Set

Posted on by
3.2b Universal Set
1. Universal set is a set that contains all the elements under consideration.
2. In set notation, the symbol ξ denotes a universal set.

Example:
Given that the universal set, ξ = {whole numbers less than 9}, A = {prime number} and B = {multiple of 4}.
(a) List all the elements of set A and set B.
(b) Illustrate the relationships between the following sets using Venn diagrams.
(i) ξ and A
(ii) ξ, A and B

Solution:
(a) ξ = {0, 1, 2, 3, 4, 5, 6, 7, 8}
 A = {2, 3, 5, 7}
 B = {4, 8}
 
(b)(i)








(b)(ii)

3.4 SPM Practice (Short Questions)

Posted on by

Question 1:

List all the subsets of set P = {r, s}.

Solution:

There are 2 elements, so the number of subsets of set P is 2n = 22 = 4.

Set P = {r, s}
Therefore subsets of set P = {r}, {s}, {r, s}, {}

Question 2:


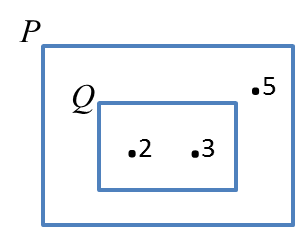
Diagram above shows a Venn diagram with the universal set,  ξ = Q ∪ P. List all the subset of set P.

Solution:

Set P has 3 elements, so the number of subsets of set P is 2n = 23 = 8.

Set P = {2, 3, 5}
Therefore subsets of set P = {}, {2}, {3}, {5}, {2, 3}, {2, 5}, {3, 5}, {2, 3, 5}.

Question 3:

It is given that the universal set, ξ = {x : 30 ≤ x < 42, x is an integer} and set P = {x : x is a number such that the sum of it its two digits is an even number}.
Find set P’.

Solution:

ξ = {30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41}
P = {31, 33, 35, 37, 39, 40}

Therefore P’ = {30, 32, 34, 36, 38, 41}

Question 4:

Given that universal set ξ = {x : 3 < x ≤ 16, x is an integer},
Set A = {4, 11, 13, 16},
Set B = {x : x is an odd number} and
Set C = {x : x is a multiple of 3}.
The elements of the set (A ∪ C)’ ∩ B are

Solution:

ξ = {4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16}
A = {4, 11, 13, 16}
B = {5, 7, 9, 11, 13, 15}
C = {6, 9, 12, 15}

(A∪C)' = {5, 6, 7, 8, 10, 14}
Therefore  (A∪C)’ ∩ B = {5, 7}

 

 

 

3.4 SPM Practice (Short Questions)

Posted on by

Question 5:

Diagram below shows a Venn diagram with the number of elements of set P, set Q and set R.

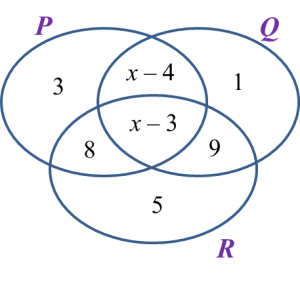
It is given that the universal set, ξ=P∪Q∪R and n(Q‘)=n(Q∩R).
Find the value of x.

Solution:

n(Q)’ = n(Q ∩ R)
3 + 8 + 5 = x– 3 + 9
16 = x + 6
x = 10

Question 6:

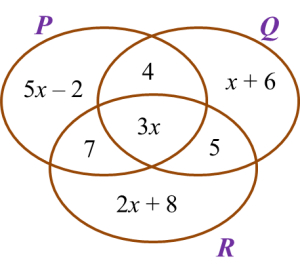
Diagram below is a Venn diagram showing the number of quiz participants in set P, set Q and set R.
It is given that the universal set, ξ=P∪Q∪R  , set P = {Science quiz participants}, set Q = {Mathematics quiz participants} and set R = {History quiz participants}.

If the number of participants who participate in only one quiz is 76, find the total number of the participants.

Solution:

Number of participants who participate in only one quiz = 76
(5x – 2) + (x + 6) + (2x + 8) = 76
8x + 12 = 76
8x = 64
x = 8
Total number of the participants
= 76 + 7 + 4 + 5 + 3(8)
= 116

Question 7:

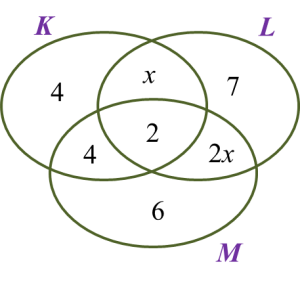
Diagram below is a Venn diagram showing the number of students in set K, set L and set M.
It is given that the universal set, ξ=K∪L∪M  , set K = {Karate Club}, set L = {Life Guards Club} and set M = {Martial Arts Club}.

If the number of students who join both the Life Guards Club and the Martial Arts Club is 8, find the number of students who join only two clubs.

Solution:

Number of students who join both the Life Guards Club and the Martial Arts Club = n(L ∩ M) = 2 + 2x
2 + 2x = 8
2x = 6
x = 3
Number of students who join only two clubs
= x + 4 + 2x
= 3 + 4 + 2(3)
= 13