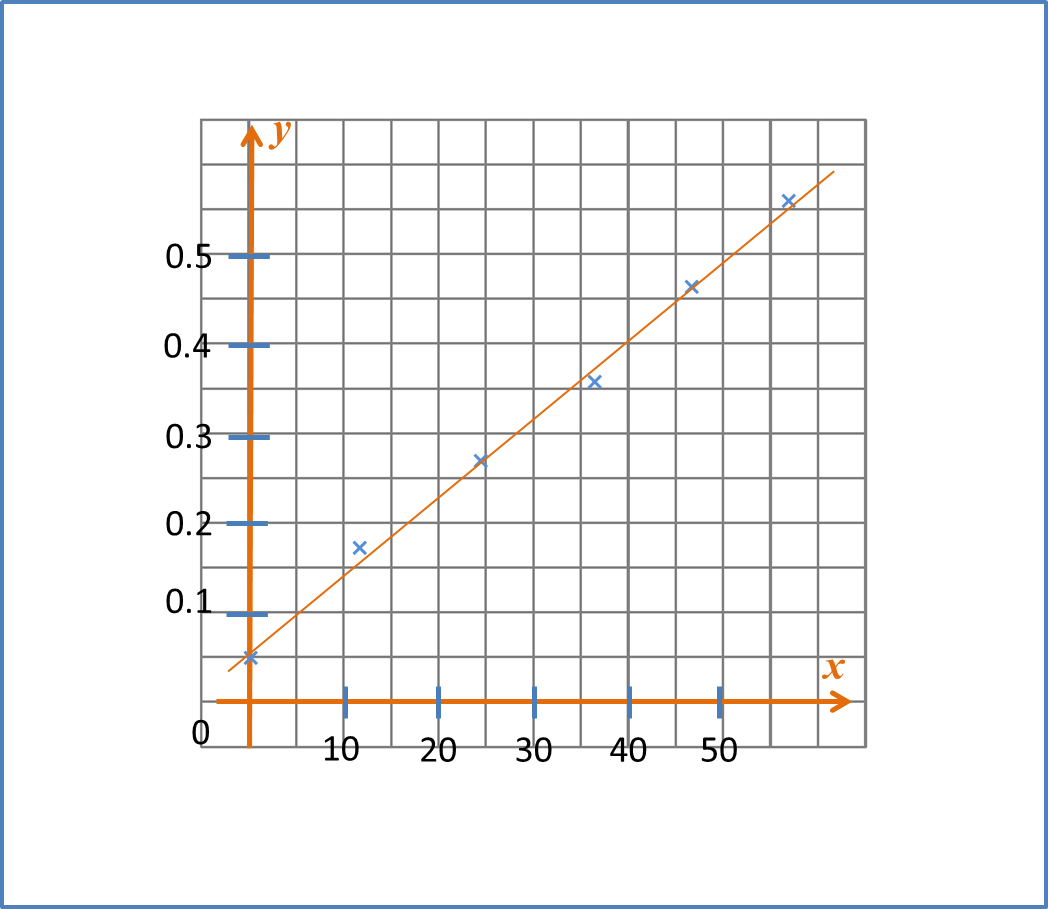
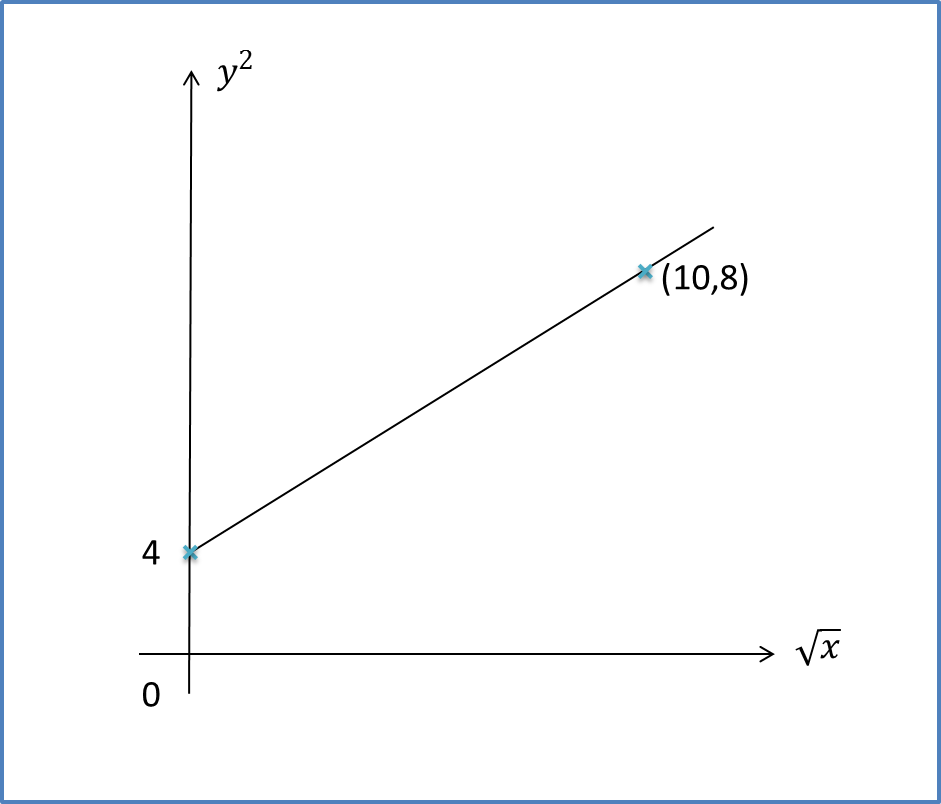
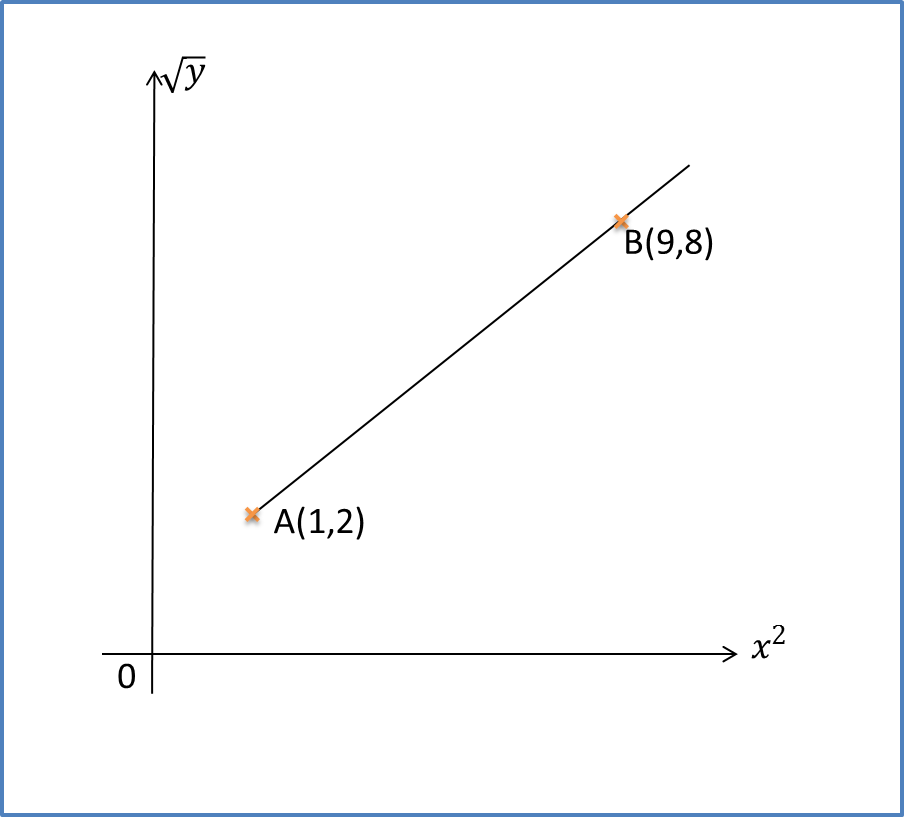
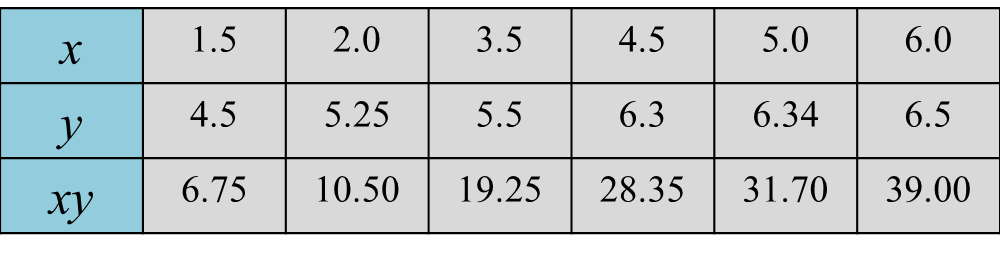
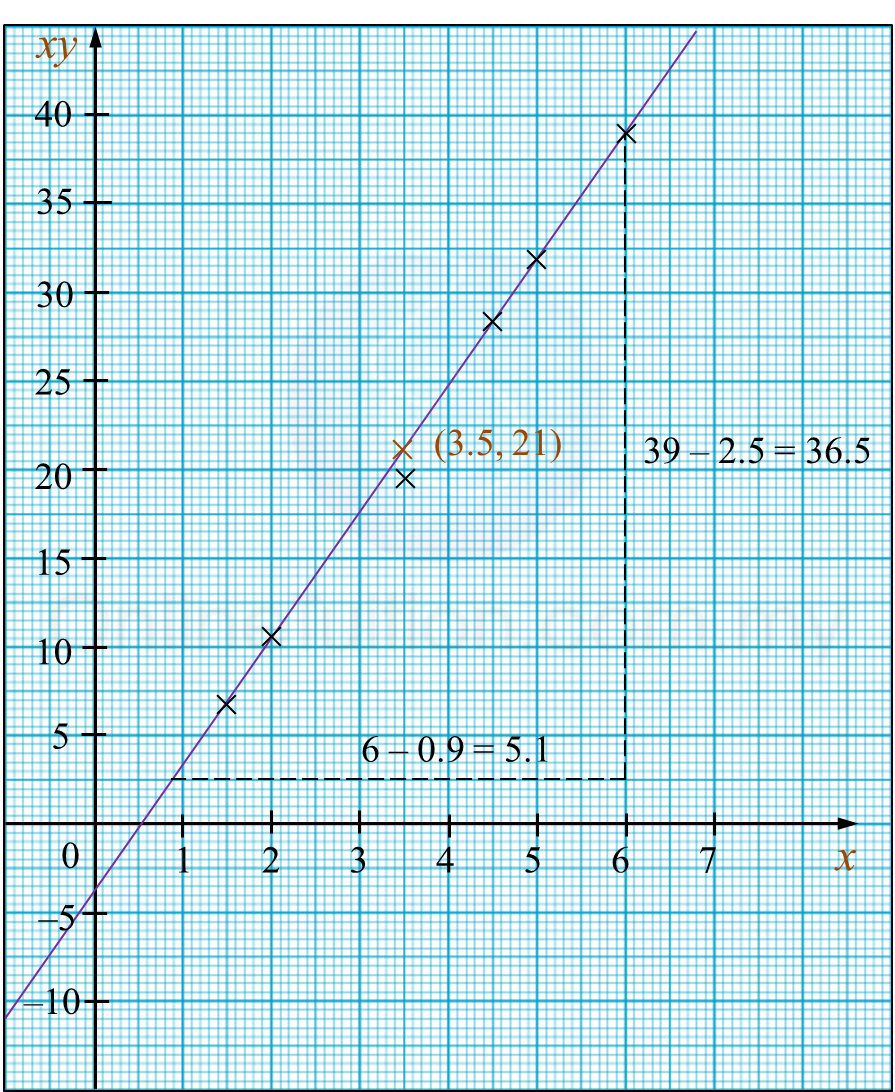
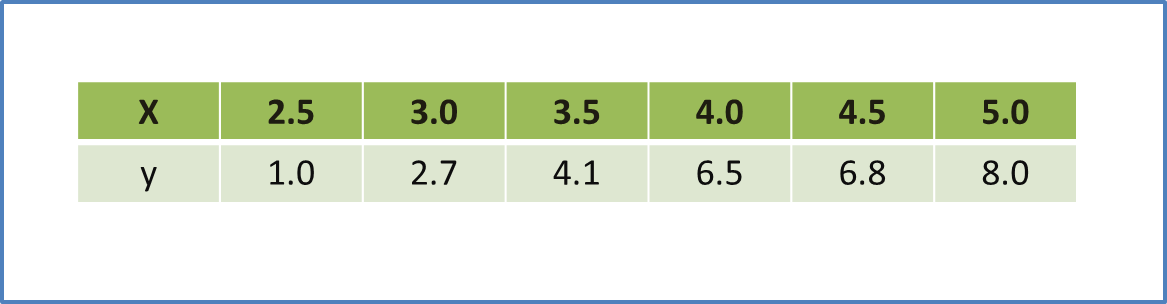
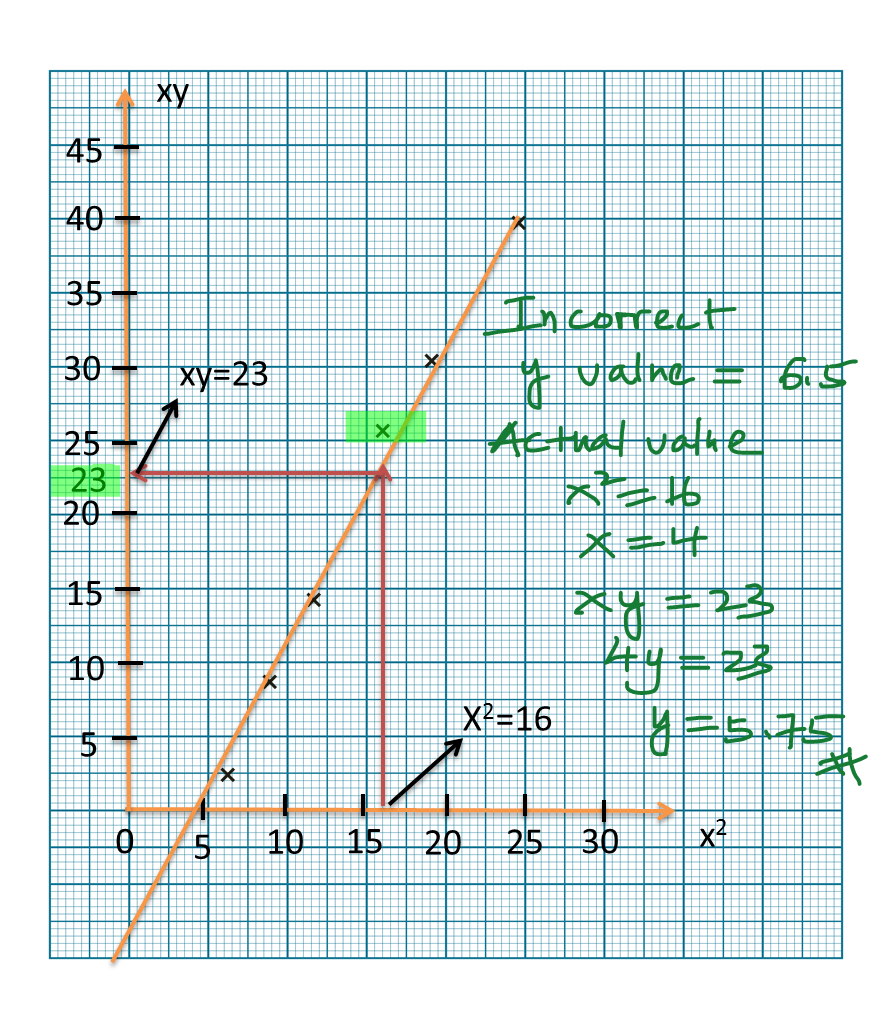
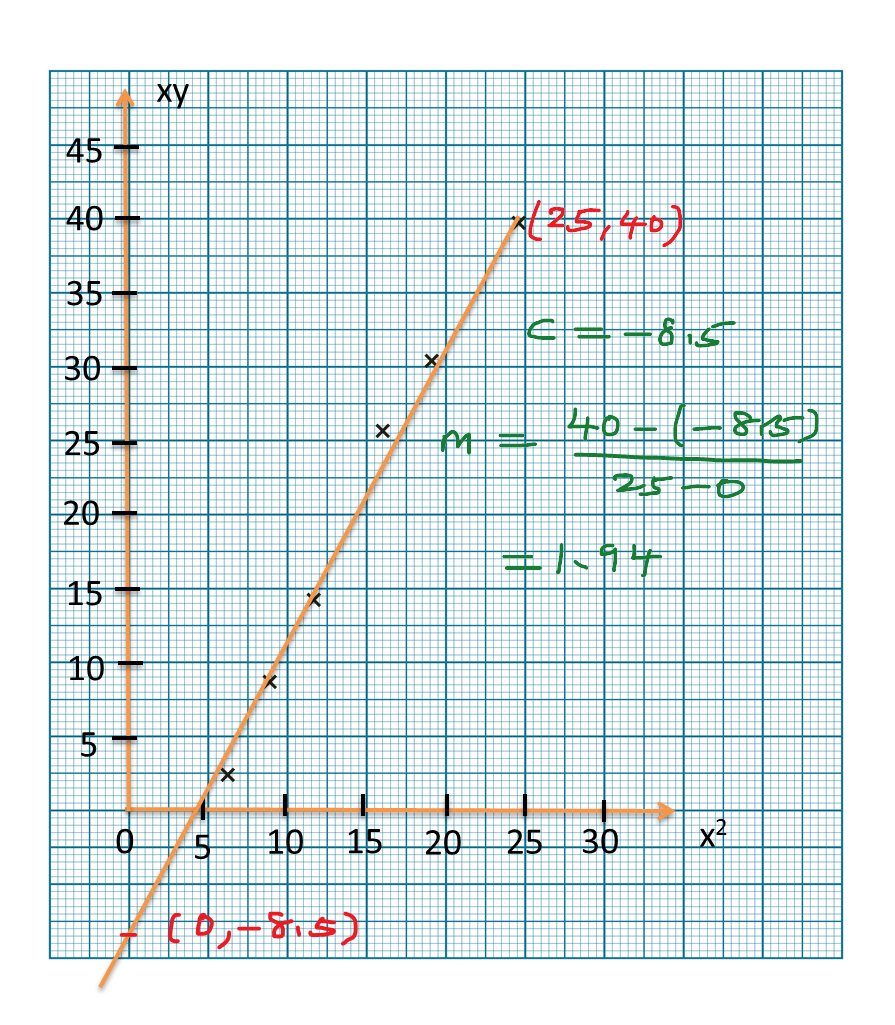
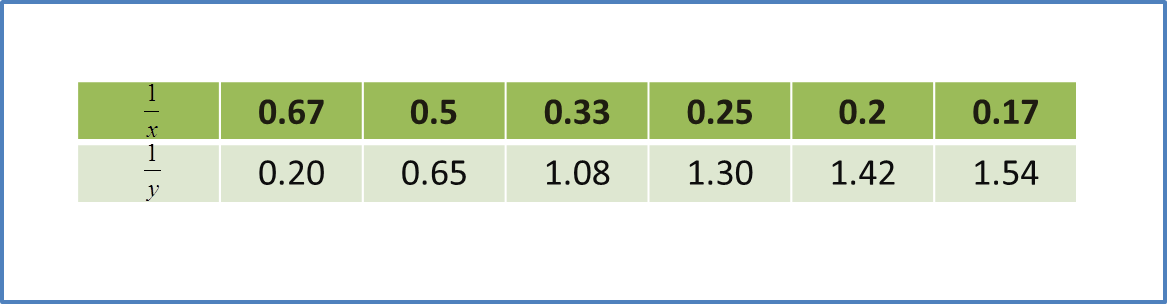
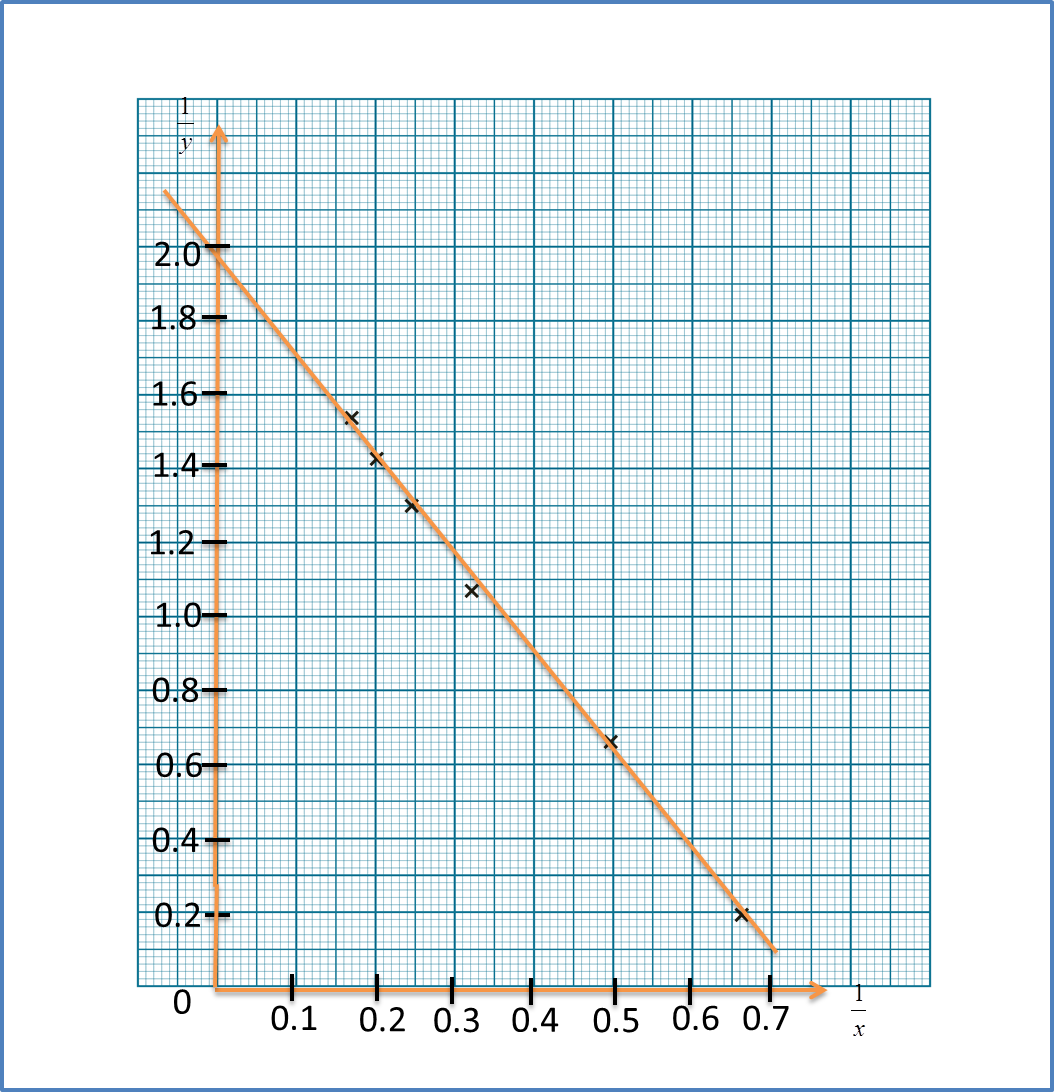
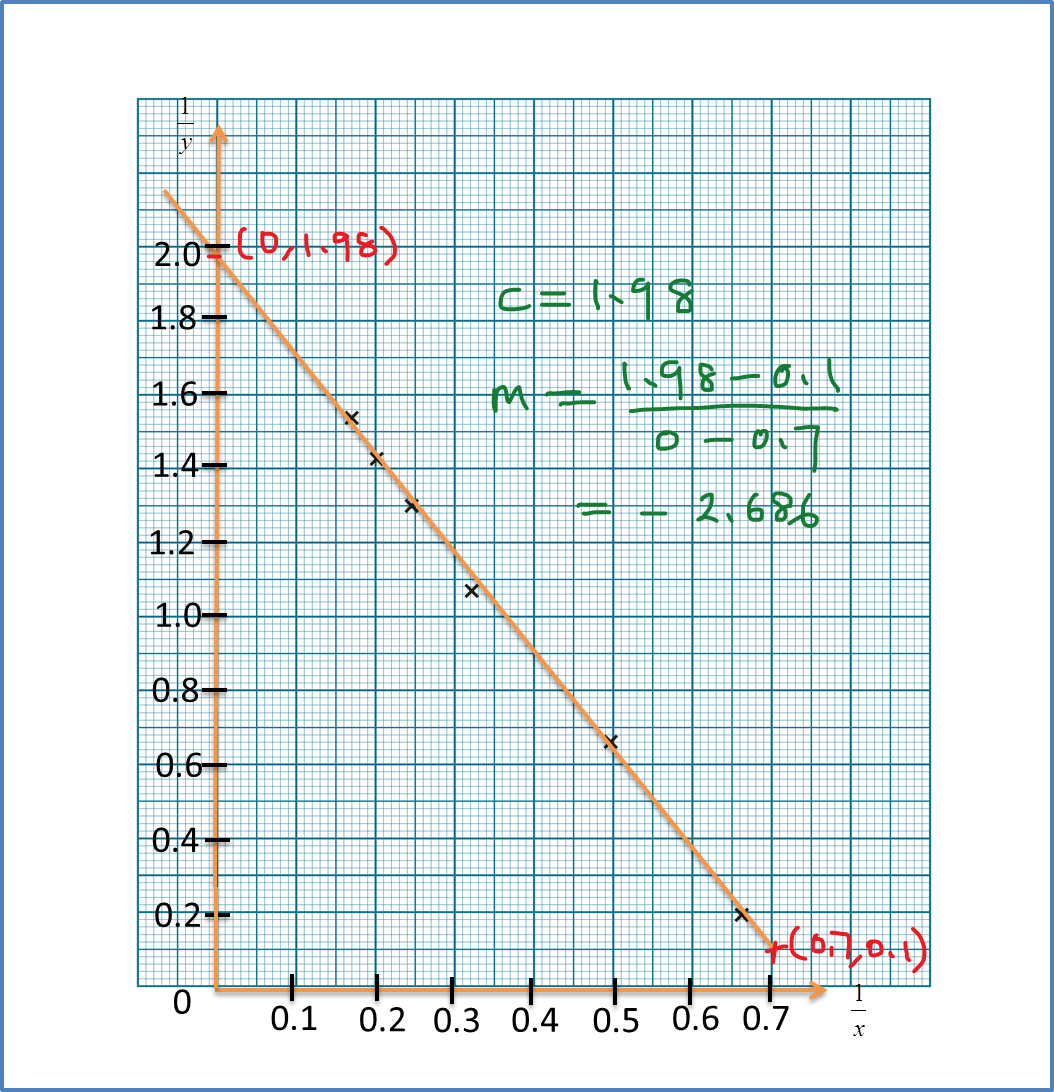
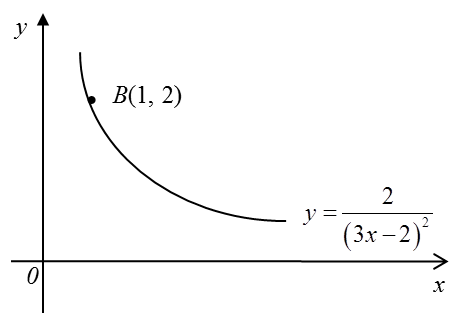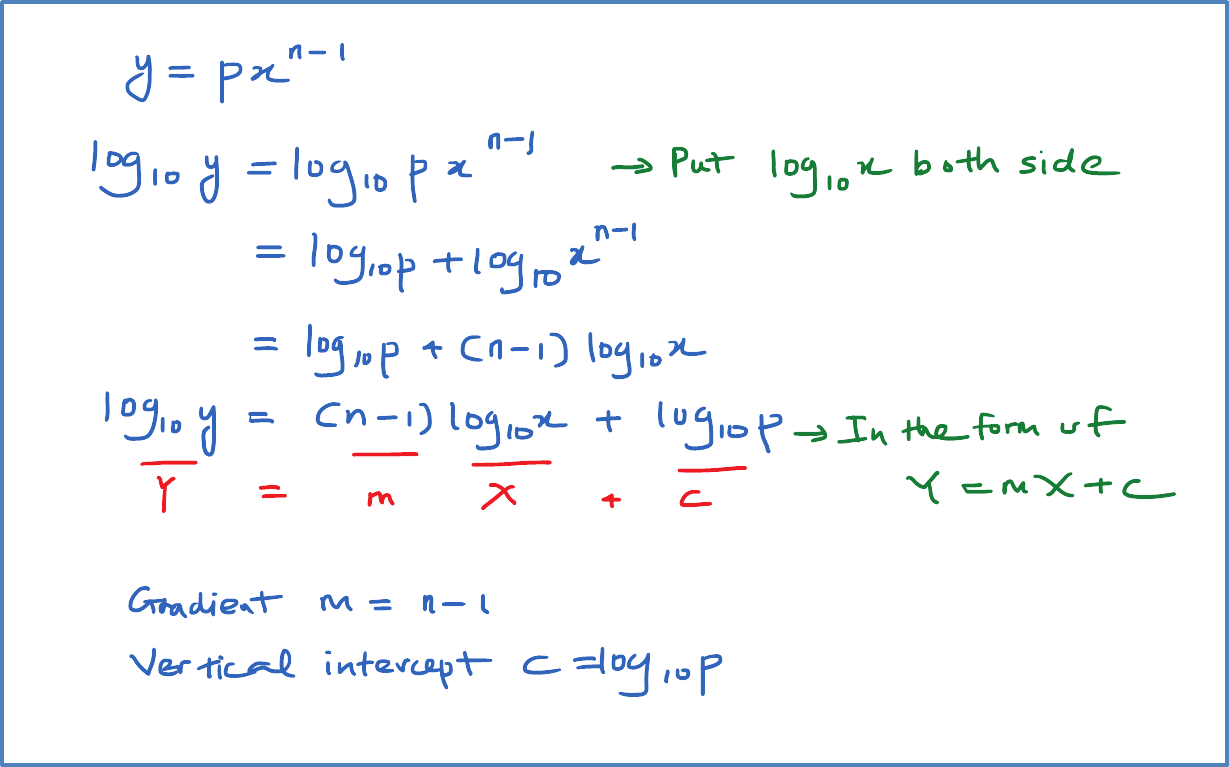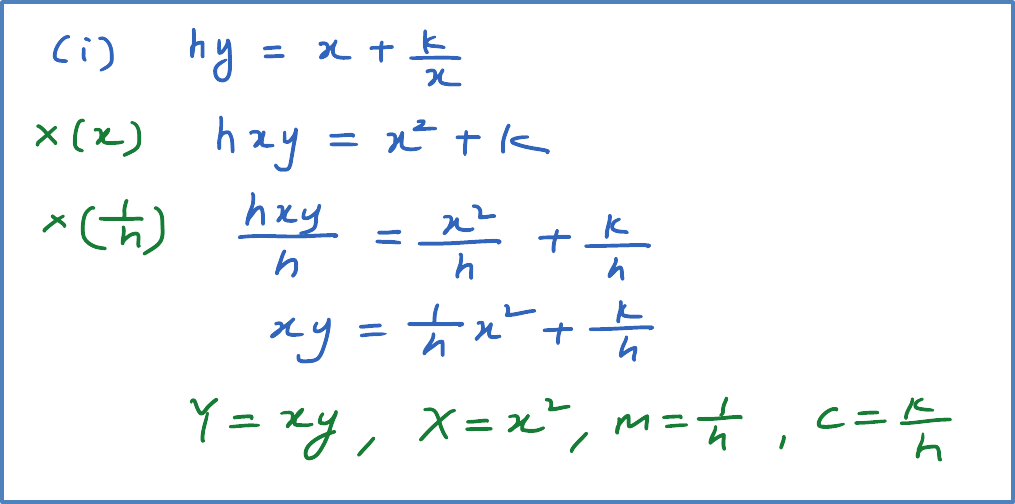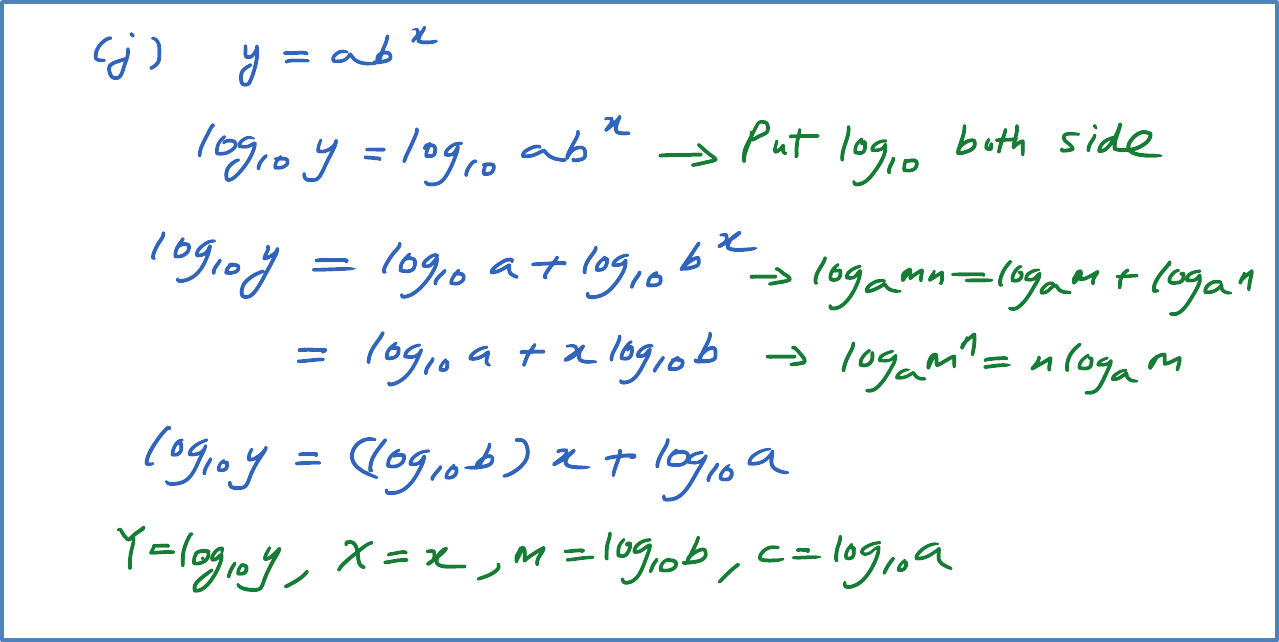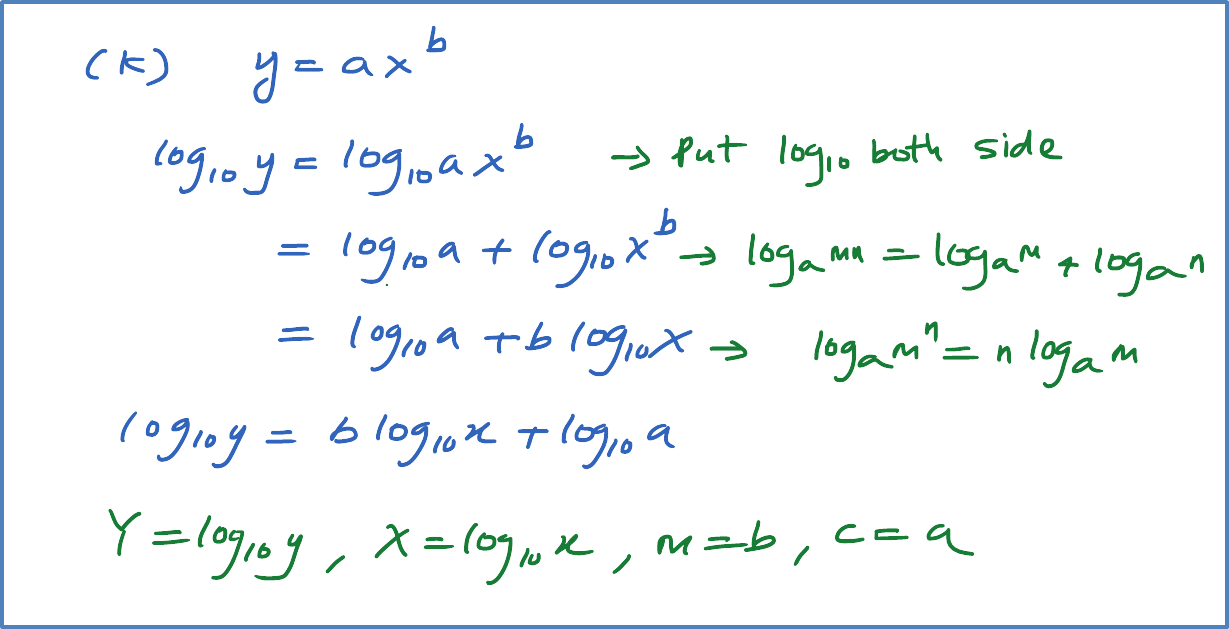Question 6:
Diagram below shows part of the curve which passes through B (1, 2).
(a) Find the equation of the tangent to the curve at the point B.
(b) A region is bounded by the curve, the x-axis and the straight lines x = 2 and x = 3.
(i) Find the area of the region.
(ii) The region is revolved through 360° about the x–axis. Find the volume generated, in terms of p.
Solution:
(a)
(b)(i)
(b)(ii)
Diagram below shows part of the curve which passes through B (1, 2).
(a) Find the equation of the tangent to the curve at the point B.
(b) A region is bounded by the curve, the x-axis and the straight lines x = 2 and x = 3.
(i) Find the area of the region.
(ii) The region is revolved through 360° about the x–axis. Find the volume generated, in terms of p.
(a)
(b)(i)
(b)(ii)