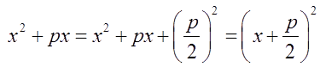2.2.2c Solving Quadratic Equations – Quadratic Formula
The quadratic equation
ax2+bx+c=0ax2+bx+c=0
can be solved by using the quadratic formula
−b±√b2−4ac2a−b±√b2−4ac2a
Example
Use the quadratic formula to find the solutions of the following equations.
a. x2+5x−24=0x2+5x−24=0
b. x(x+4)=10x(x+4)=10
Answer
(a)
For the equation x2+5x−24=0x2+5x−24=0
(b)
x(x+ 4) = 10x2+4x−10=0a=1, b=4, c=−10x=−b±√b2−4ac2ax=−(4)±√(4)2−4(1)(−10)2(1)x=−4±√562x=1.742 or x=−5.742x(x+ 4) = 10x2+4x−10=0a=1, b=4, c=−10x=−b±√b2−4ac2ax=−(4)±√(4)2−4(1)(−10)2(1)x=−4±√562x=1.742 or x=−5.742
−b±√b2−4ac2a−b±√b2−4ac2a
Example
Use the quadratic formula to find the solutions of the following equations.
a. x2+5x−24=0x2+5x−24=0
b. x(x+4)=10x(x+4)=10
Answer
(a)
For the equation x2+5x−24=0x2+5x−24=0
a = 1, b = 5, c = -24
x=−b±√b2−4ac2ax=−(5)±√(5)2−4(1)(−24)2(1)x=−5±√1212x=−8 or x=3x=−b±√b2−4ac2ax=−(5)±√(5)2−4(1)(−24)2(1)x=−5±√1212x=−8 or x=3
(b)
x(x+ 4) = 10x2+4x−10=0a=1, b=4, c=−10x=−b±√b2−4ac2ax=−(4)±√(4)2−4(1)(−10)2(1)x=−4±√562x=1.742 or x=−5.742x(x+ 4) = 10x2+4x−10=0a=1, b=4, c=−10x=−b±√b2−4ac2ax=−(4)±√(4)2−4(1)(−10)2(1)x=−4±√562x=1.742 or x=−5.742
2.2b Solving Quadratic Equations – Completing the Square (Examples)
2.4.2a Solving Quadratic Equations – Completing the Square (Examples)
(A) Steps to solve quadratic equation using completing the square
• make sure that the coefficient of x is 1.
• Rewrite the equation ax2 + bx + c = 0 in the form ax2 + bx = –c.
• Add (coefficient of x2)2(coefficient of x2)2 to both side of the equation.
• make sure that the coefficient of x is 1.
• Rewrite the equation ax2 + bx + c = 0 in the form ax2 + bx = –c.
• Add (coefficient of x2)2(coefficient of x2)2 to both side of the equation.
Example:
Solve the following quadratic equations by completing the square.
(a) x2 – 6x – 3 = 0
(a) x2 – 6x – 3 = 0
(b) 2x2 – 5x – 7 = 0
(c) x2 + 1 = 10x/3
Solution:
2.2b Solving Quadratic Equations – Completing the Square
2.4.2 Solving Quadratic Equations – Completing the Square
(A) The Perfect Square
(A) The Perfect Square
1. The expression x2 + 2x + 1 can be written in the form (x + 1)2, it is called a “perfect square”.
2. If the algebraic expression on the left hand side of the quadratic equation is a perfect, the roots can be easily obtained by finding the square roots.
2. If the algebraic expression on the left hand side of the quadratic equation is a perfect, the roots can be easily obtained by finding the square roots.
Example:
Solve each of the following quadratic equation
Solve each of the following quadratic equation
(a) (x + 1)2 = 25
(b) x2 − 8x + 16 = 49
Solution:
(a)
(x + 1)2 = 25
(x + 1)2 = ±√25
x = −1 ± 5
x = 5 or x = −6
(b)
x2 − 8x + 16 = 49
(x − 4)2 = 49
(x − 4) = ±√49
x = 4 ± 7
x = 11 or x = −3
(B) Solving Quadratic Equation by Completing the Square
1. To solve quadratic equation, we make the left hand side of the equation a perfect square.
2. To make any quadratic expression x2 + px into a perfect square, we add the term (p/2)2 to the expression and this will make
3. The following shows the steps to solve the equation by using completing the square method for quadratic equation ax2+ bx = – c.
(a) Rewrite the equation in the form ax2 + bx = – c.
(b) If the coefficient a ≠ 1, reduce it to 1 (by dividing).
(c) Add (p/2)2 to both sides of the equation.
(d) Write the expression on the left hand side as a perfect square.
(e) Solve the equation.
Solving Quadratic Equations
Solving Quadratic Equations
To solve a quadratic equation means to find all the roots of the quadratic equations.Example:
Find the roots of the quadratic equations
a. x2=9x2=9
b. 2x2−98=02x2−98=0
Answer:
(a)
x2=9x=±√9x=±3x2=9x=±√9x=±3
(b)
2x2−98=02x2=98x2=982=49x=±√49=±72x2−98=02x2=98x2=982=49x=±√49=±7
Roots of Quadratic Equation – Example
Remember : Roots of a quadratic equation are the values of variables/unknowns that satisfy the equation.
Example
(a) Given x = 3 is the root of the quadratic equation x2+2x+p=0x2+2x+p=0 , find the value of p.
(b) The roots of the quadratic equation 3x2+hx+k=03x2+hx+k=0 are -2 and 4. Find the value of h and k.
Example
(a) Given x = 3 is the root of the quadratic equation x2+2x+p=0x2+2x+p=0 , find the value of p.
(b) The roots of the quadratic equation 3x2+hx+k=03x2+hx+k=0 are -2 and 4. Find the value of h and k.
General Form of Quadratic Equation
General Form of Quadratic Equation
General form of a quadratic equation is
ax2+bx+c=0ax2+bx+c=0
where a, b, and c are constants and a≠0.
*Note that the highest power of an unknown of a quadratic equation is 2.
General form of a quadratic equation is
ax2+bx+c=0ax2+bx+c=0
where a, b, and c are constants and a≠0.
*Note that the highest power of an unknown of a quadratic equation is 2.
Quadratic Equations (Introduction)
What is a Quadratic Equation?
- A quadratic equation is a polynomial equation of the second degree.
- A quadratic equation has only one variable
- The highest power of the variable is 2.
The followings are some examples of quadratic equations
- 2x2+3x+4=02x2+3x+4=0
- t2=25t2=25
- y(6y−3)=5y(6y−3)=5
- a−3y+2y2=2a−3y+2y2=2 where a is a constant.
Example of Non Quadratic Equation
- 2x+1=02x+1=0 , (Reason: The highest power of x ≠ 2.)
- 2x3+1=x2x3+1=x , (Reason: The highest power of x ≠ 2.)
- t2+5t=3t2+5t=3 , (Reason: The present of the term 5t5t .)
SPM Practice (Long Question)
Question 5:
In diagram below, the function g maps set P to set Q and the function h maps set Q to set R.

Find
(a) in terms of x, the function
(i) which maps set Q to set P,
(ii) h(x).
(b) the value of x such that gh(x) = 8x + 1.
Solution:
(a)(i)
g(x)=3x+2Let g−1(x)=yg(y)=x3y+2=x y=x−23g−1(x)=x−23g(x)=3x+2Let g−1(x)=yg(y)=x3y+2=x y=x−23g−1(x)=x−23
(a)(ii)
hg(x)=12x+5h(3x+2)=12x+5→g(x)=3x+2Let u=3x+2 x=u−23h(u)=12(u−23)+5 =4u−8+5 =4u−3h(x)=4x−3
(b)
gh(x)=g(4x−3) =3(4x−3)+2 =12x−9+2 =12x−712x−7=8x+1 4x=8 x=2
In diagram below, the function g maps set P to set Q and the function h maps set Q to set R.

Find
(a) in terms of x, the function
(i) which maps set Q to set P,
(ii) h(x).
(b) the value of x such that gh(x) = 8x + 1.
Solution:
(a)(i)
g(x)=3x+2Let g−1(x)=yg(y)=x3y+2=x y=x−23g−1(x)=x−23g(x)=3x+2Let g−1(x)=yg(y)=x3y+2=x y=x−23g−1(x)=x−23
(a)(ii)
hg(x)=12x+5h(3x+2)=12x+5→g(x)=3x+2Let u=3x+2 x=u−23h(u)=12(u−23)+5 =4u−8+5 =4u−3h(x)=4x−3
(b)
gh(x)=g(4x−3) =3(4x−3)+2 =12x−9+2 =12x−712x−7=8x+1 4x=8 x=2