Question 3:
(b)(i) Sketch the graph of y = – tan 2x for 0 ≤ x ≤ π .
(b)(ii) Hence, by drawing a suitable straight line on the same axes, find the number of solutions satisfying the equation 3xπ+2tanx2−sec2x=0 for 0 ≤ x ≤ π .
Solution:
(a)
2tanx2−sec2x=tan2xLHS:2tanx2−sec2x=2tanx2−(1+tan2x)=2tanx2−tan2x=tan2x(RHS)
(b)(i)
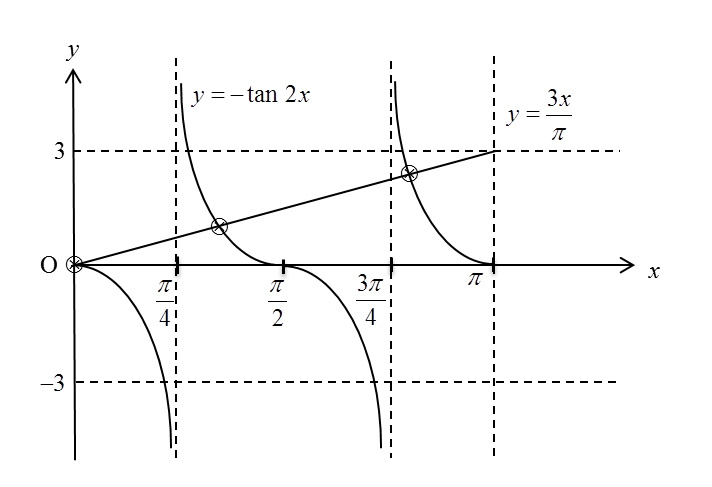
(b)(ii)
3xπ+2tanx2−sec2x=03xπ+tan2x=0←from part (a)−tan2x=3xπ y=3xπThe suitable straight line to sketch is y=3xπ.
When x = 0, y = 0.
(a) Prove that
2tanx2−sec2x=tan2x.
(b)(i) Sketch the graph of y = – tan 2x for 0 ≤ x ≤ π .
(b)(ii) Hence, by drawing a suitable straight line on the same axes, find the number of solutions satisfying the equation 3xπ+2tanx2−sec2x=0 for 0 ≤ x ≤ π .
State the number of solutions.
Solution:
2tanx2−sec2x=tan2xLHS:2tanx2−sec2x=2tanx2−(1+tan2x)=2tanx2−tan2x=tan2x(RHS)
(b)(i)
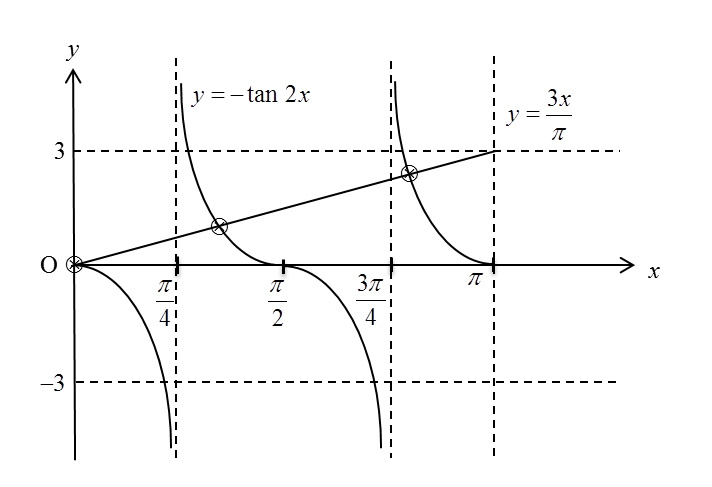
3xπ+2tanx2−sec2x=03xπ+tan2x=0←from part (a)−tan2x=3xπ y=3xπThe suitable straight line to sketch is y=3xπ.
When x = 0, y = 0.
When x = π, y = 3.
Number of solutions = 3