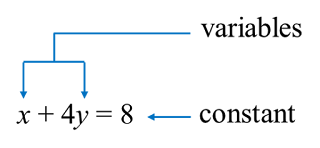
Question 6:
List all the integer values of x which satisfy the following linear inequalities:
–2 < 3x + 1 ≤ 10
Solution:
–2 < 3x + 1
–3 < 3x
x > –1
x = 0, 1, 2, 3, …
3x + 1 ≤ 10
3x ≤ 9
x ≤ 3
x = 3, 2, 1, 0, …
Therefore x = 0, 1, 2, 3
List all the integer values of x which satisfy the following linear inequalities:
–2 < 3x + 1 ≤ 10
Solution:
–2 < 3x + 1
–3 < 3x
x > –1
x = 0, 1, 2, 3, …
3x + 1 ≤ 10
3x ≤ 9
x ≤ 3
x = 3, 2, 1, 0, …
Therefore x = 0, 1, 2, 3
Question 7:
List all the integer values of x which satisfy the following linear inequalities:
–5 < 2x – 3 ≤ 1
Solution:
–5 < 2x – 3
–5 + 3 < 2x
2x > –2
x > –1
x = 0, 1, 2, 3, …
2x – 3 ≤ 1
2x ≤ 4
x ≤ 2
x = 2, 1, 0, –1, …
Therefore x = 0, 1, 2
List all the integer values of x which satisfy the following linear inequalities:
–5 < 2x – 3 ≤ 1
Solution:
–5 < 2x – 3
–5 + 3 < 2x
2x > –2
x > –1
x = 0, 1, 2, 3, …
2x – 3 ≤ 1
2x ≤ 4
x ≤ 2
x = 2, 1, 0, –1, …
Therefore x = 0, 1, 2
Question 8:
Solution:
Solution:
Question 9:
Find the biggest and the smallest integer of x that satisfy
3x + 2 ≥ –4 and 4 – x > 0.
Solution:
3x + 2 ≥ –4
3x ≥ –4 – 2
3x ≥ –6
x ≥ –2
4 – x > 0
–x > –4
x < 4
Smallest integer of x is –2, and the biggest integer of x is 3.
Find the biggest and the smallest integer of x that satisfy
3x + 2 ≥ –4 and 4 – x > 0.
Solution:
3x + 2 ≥ –4
3x ≥ –4 – 2
3x ≥ –6
x ≥ –2
4 – x > 0
–x > –4
x < 4
Smallest integer of x is –2, and the biggest integer of x is 3.
Question 10:
Solution:
Solution:




 Diagram 2.1
Diagram 2.1 Diagram 2.2
Diagram 2.2