Bab 7 Statistik

Posted on May 31, 2016 by user

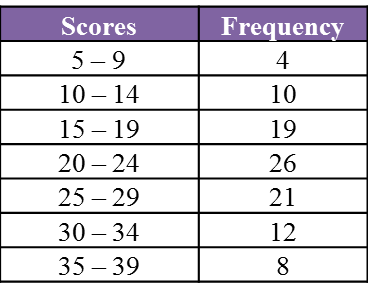
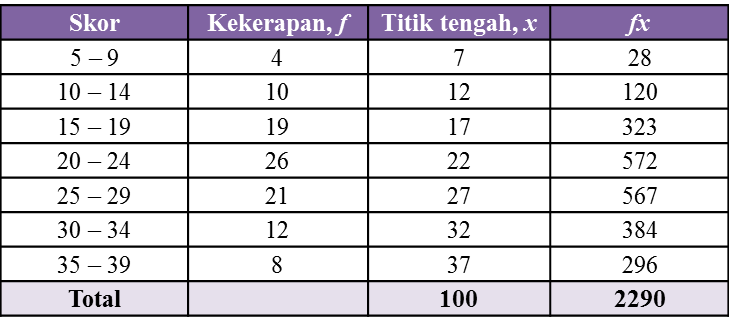
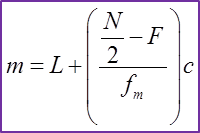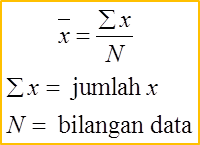7.4.1 Statistik, SPM Praktis (Kertas 2)

Soalan 1:

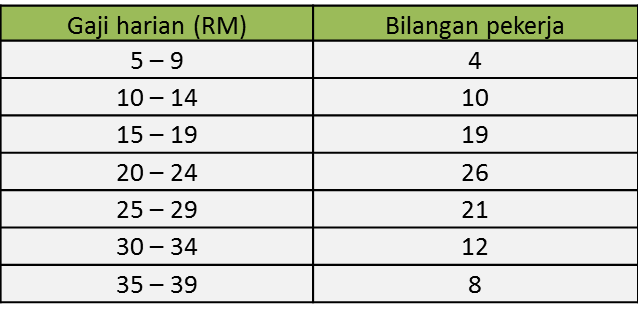
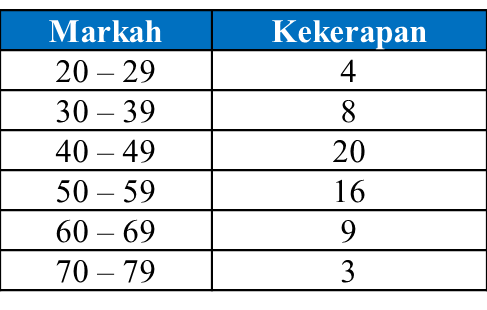
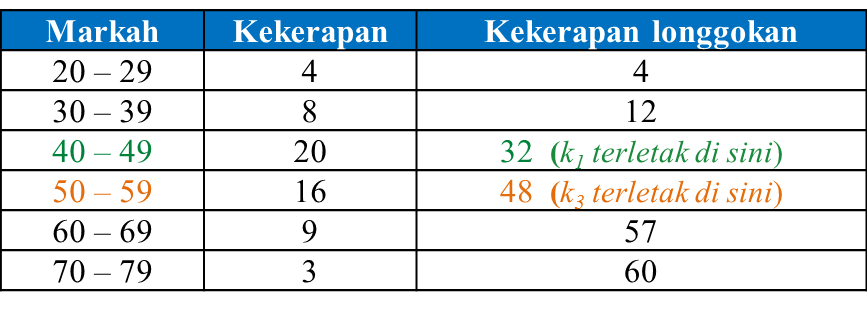
Jadual di bawah menunjukkan umur 40 orang pelancong melawat suatu tempat pelancongan.

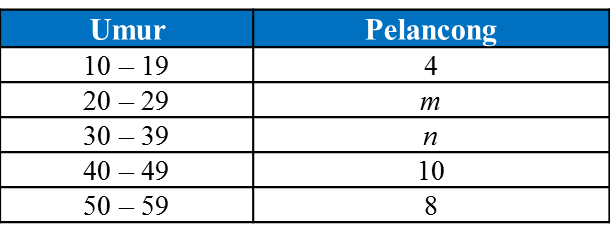
Diberi umur median ialah 35.5, cari nilai m dan n.

Penyelesaian:

Diberi umur median ialah 35.5,

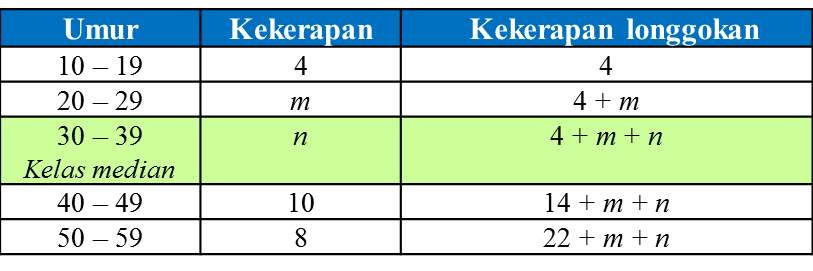
22 + m + n = 40

n = 18 – m -----(1)

Diberi umur median = 35.5, maka kelas median ialah 30 – 39.

\begin{array}{l} 35.5 = 29.5 + (\frac{20 - (4 + m)}{n}) \times 10 \\ 6 = (\frac{16 - m}{n}) \times 10 \end{array}

6n = 160 – 10m

3n = 80 – 5m -----(2)

Gantikan (1) ke dalam (2).

3 (18 – m) = 80 – 5m

54 – 3m = 80 – 5m

2m = 26

m = 13

Ganti m = 13 ke dalam (1).

n = 18 – 13

n = 5

Dengan itu, m = 13, n = 5.

Soalan 2:

Satu set markah ujian x₁, x₂, x₃, x₄, x₅, x₆ mempunyai min 6 dan sisihan piawai 2.4.

(a) Cari

(i) hasil tambah markah itu, ∑x,

(ii) hasil tambah kuasa dua markah itu, ∑x².

(b) Setiap markah itu didarab dengan 2 dan kemudian ditambah dengan 3. Cari bagi set markah baru itu,

(i) min,

(ii) varians.

Penyelesaian:

(a)(i)

\begin{array}{l} Diberi min = 6 \\ \frac{Σ x}{6} = 6 \\ Σ x = 36 \end{array}

(a)(ii)

\begin{array}{l} Diberi σ = 2.4 \\ σ^{2} = {2.4}^{2} \\ \frac{Σ x^{2}}{n} - {\bar{X}}^{2} = 5.76 \\ \frac{Σ x^{2}}{6} - 6^{2} = 5.76 \\ \frac{Σ x^{2}}{6} = 41.76 \\ Σ x^{2} = 250.56 \end{array}

(b)(i)

Markah min baru

= 6(2) + 3

= 15

(b)(ii)

Varians bagi set markah asal

= 2.4²= 5.76

Varians bagi set markah baru

= 2² (5.76)

= 23.04

Bab 7 Statistik

Posted on May 31, 2016 by user

7.3 Statistik, SPM Praktis (Kertas 1)

Soalan 3:

Min bagi lima nombor ialah

\sqrt{p}

. hasil tambah bagi kuasa dua nombor-nombor itu ialah 120 dan sisihan piawai ialah 2q. Ungkap p dalam sebutan q.

Penyelesaian:

\begin{array}{l} Min \bar{x} = \frac{\sum x}{N} \\ \sqrt{p} = \frac{\sum x}{5} \\ \sum x = 5 \sqrt{p} \\ Sisihan piawai, σ = \sqrt{\frac{\sum x^{2}}{N} - {\bar{x}}^{2}} \\ 2 q = \sqrt{\frac{120}{5} - {(\sqrt{p})}^{2}} \\ 4 q^{2} = 24 - p \\ p = 24 - 4 q^{2} \end{array}

Soalan 4:

Satu set integer positif terdiri daripada 1, 4 dan p. Varians bagi set integer ini ialah 6. Cari nilai p.

Penyelesaian:

\begin{array}{l} Varians, σ^{2} = \frac{\sum x^{2}}{N} - {\bar{x}}^{2} \\ 6 = \frac{1^{2} + 4^{2} + p^{2}}{3} - {(\frac{1 + 4 + p}{3})}^{2} \\ 6 = \frac{17 + p^{2}}{3} - {(\frac{5 + p}{3})}^{2} \\ 6 = \frac{17 + p^{2}}{3} - [\frac{25 + 10 p + p^{2}}{9}] \\ 6 = \frac{51 + 3 p^{2} - 25 - 10 p - p^{2}}{9} \end{array}

2p² – 10p + 26 = 54

2p² – 10p + 28 = 0

p² – 5p + 14 = 0

(p – 7)(p + 2) = 0

p= –2 (tidak diterima)

Maka p = 7

Bab 7 Statistik

Posted on May 31, 2016 by user

7.3 Statistik, SPM Praktis (Kertas 1)

Soalan 1:

Sisihan piawai bagi lima nombor ialah 6 dan hasil tambah bagi kuasa dua nombor-nombor itu ialah 260. Cari min bagi set nombor itu.

Penyelesaian:

\begin{array}{l} Diberi σ = 6, Σ x^{2} = 260. \\ σ = 6 \\ \sqrt{\frac{Σ x^{2}}{n} - {\bar{X}}^{2}} = 6 \\ \frac{Σ x^{2}}{n} - {\bar{X}}^{2} = 36 \\ \frac{260}{5} - {\bar{X}}^{2} = 36 \\ {\bar{X}}^{2} = 16 \\ \bar{X} = \pm 4 \\ ∴ min = \pm 4 \end{array}

Soalan 2:

Kedua-dua min dan sisihan piawai bagi set nombor 1, 3, 7, 15, m dan n ialah 6. Cari

(a) nilai m+ n,

(b) nilai yang mungkin bagi n.

Penyelesaian:

(a)

\begin{array}{l} Diberi min = 6 \\ \frac{Σ x}{n} = 6 \\ \frac{Σ x}{6} = 6 \end{array}

1 + 3 + 7 + 15 + m + n= 36

26 + m + n = 36

m + n = 10

(b)

\begin{array}{l} σ = 6 \\ σ^{2} = 36 \\ \frac{Σ x^{2}}{n} - {\bar{X}}^{2} = 36 \\ \frac{1 + 9 + 49 + 225 + m^{2} + n^{2}}{6} - 6^{2} = 36 \\ \frac{284 + m^{2} + n^{2}}{6} - 36 = 36 \\ \frac{284 + m^{2} + n^{2}}{6} = 72 \end{array}

284 + m² + n² = 432

m² + n² = 148

Daripada (a), m = 10 – n

(10 – n)² + n² = 148

100 – 20n + n²+ n² = 148

2n² – 20n – 48 = 0

n² – 10n – 24 = 0

(n – 6)(n + 4) = 0

n = 6 atau n = –4

Bab 7 Statistik

Posted on May 31, 2016 by user

7.1c Median

1. Median ialah nilai yang terletak di tengah-tengah sesuatu set data setelah set data itu disusun mengikut tertib tertentu.

(A) Data Tak Terkumpul

Median, m = C e r a p a n_{\frac{n + 1}{2}}

Contoh 1:

Cari median bagi setiap set data yang berikut.

(a) 15, 18, 21, 25, 20, 18

(b) 13, 6, 9, 17, 11

Penyelesaian:

(a)

Susun data mengikut tertib menaik

15, 18, 18, 20, 21, 25

\begin{array}{l} Median \\ = C e r a p a n_{\frac{n + 1}{2}} = C e r a p a n_{\frac{6 + 1}{2}} = C e r a p a n_{3 \frac{1}{2}} \\ = \frac{18 + 20}{2} = 19 \end{array}

(b)

6, 9, 11, 13, 17

\begin{array}{l} Median \\ = C e r a p a n_{\frac{n + 1}{2}} = C e r a p a n_{\frac{5 + 1}{2}} = C e r a p a n_{3} \\ = 11 \end{array}

(B) Data Terkumpul (tanpa Selang Kelas)

Median, m = C e r a p a n_{\frac{n + 1}{2}}

Contoh 2:

Jadual kekerapan yang berikut menunjukkan markah ujian biologi bagi 40 orang pelajar.

Hitung markah median.

Penyelesaian:

\begin{array}{l} Median \\ = C e r a p a n_{\frac{n + 1}{2}} = C e r a p a n_{\frac{40 + 1}{2}} = C e r a p a n_{20 \frac{1}{2}} \\ = 60 \leftarrow (C e r a p a n ke- 20 \frac{1}{2} ialah 60 markah) \end{array}

(C) Data Terkumpul (dengan Selang Kelas)

m = median

L = sempadan bawah kelas median

N = jumlah kekerapan

F = kekerapan longgokan sebelum kelas median

f_m = kekerapan kelas median

c = saiz kelas median (Sempadan atas kelas – sempadan bawah kelas)

1. Median boleh ditentukan daripada jadual kekerapan longgokan dan ogif.

Contoh 3:

Jadual yang berikut menunjukkan taburan skor yang diperoleh 100 orang pelajar tingkatan 4 dalam satu pertandingan.

Cari median.

Penyelesaian:

Kaedah 1: guna rumus

Langkah 1:

\begin{array}{l} Kelas median \\ = C e r a p a n_{\frac{n}{2}} = C e r a p a n_{\frac{100}{2}} = C e r a p a n_{50} \\ Maka kelas median berada di 20 - 24 \end{array}

Langkah 2:

\begin{array}{l} m = L + (\frac{\frac{N}{2} - F}{f_{m}}) c \\ m = 19.5 + (\frac{\frac{100}{2} - 33}{26}) 5 \\ m = 19.5 + 3.269 = 22.77 \end{array}

Bab 7 Statistik

Posted on May 31, 2016 by user

7.2 Sukatan Serakan (Bahagian 3)

7.2c Varians dan Sisihan Piawai

1. Varians ialah sukatan minbagi kuasa dua sisihan-sisihan daripada min.

2. Sisihan piawai merujuk kepada punca kuasa dua positif bagi varians.

(A) Data Tak Terkumpul

Varians, σ^{2} = \frac{\sum x^{2}}{N} - {\bar{x}}^{2}

Sisihan piawai, σ = \sqrt{varians}

Contoh 1:

Cari varians dan sisihan piawai bagi set data,

15, 17, 21, 24 dan 31

Penyelesaian:

\begin{array}{l} Varians, σ^{2} = \frac{\sum x^{2}}{N} - {\bar{x}}^{2} \\ σ^{2} = \frac{15^{2} + 17^{2} + 21^{2} + 24^{2} + 31^{2}}{5} \\ - {(\frac{15 + 17 + 21 + 24 + 31}{5})}^{2} \\ σ^{2} = \frac{2492}{5} - {21.6}^{2} \\ σ^{2} = 31.84 \\ Sisihan piawai, σ = \sqrt{varians} \\ σ = \sqrt{31.84} \\ σ = 5.642 \end{array}

(B) Data Terkumpul (tanpa Selang Kelas)

Varians, σ^{2} = \frac{\sum f x^{2}}{\sum f} - {\bar{x}}^{2}

Sisihan piawai, σ = \sqrt{varians}

Contoh 2:

Data di bawah menunjukkan bilangan kanak-kanak oleh 30 keluarga:

Bilangan kanak-kanak	2	3	4	5	6	7	8
Kekerapan	6	8	5	3	3	3	2

Cari varians dan sisihan piawai bagi set data.

Penyelesaian:

\begin{array}{l} Min \bar{x} = \frac{\sum f x}{\sum f} \\ = \frac{(6) (2) + (8) (3) + (5) (4) + (3) (5) + (3) (6) + (3) (7) + (2) (8)}{6 + 8 + 5 + 3 + 3 + 3 + 2} \\ = \frac{126}{30} = 4.2 \\ \frac{\sum f x^{2}}{\sum f} \\ = \frac{(6) {(2)}^{2} + (8) {(3)}^{2} + (5) {(4)}^{2} + (3) {(5)}^{2} + (3) {(6)}^{2} + (3) {(7)}^{2} + (2) {(8)}^{2}}{6 + 8 + 5 + 3 + 3 + 3 + 2} \\ = \frac{634}{30} = 21.13 \end{array}

\begin{array}{l} Varians, σ^{2} = \frac{\sum f x^{2}}{\sum f} - {\bar{x}}^{2} \\ σ^{2} = 21.133 - {4.2}^{2} \\ σ^{2} = 3.493 \\ Sisihan piawai, σ = \sqrt{varians} \\ σ = \sqrt{3.493} \\ σ = 1 .869 \end{array}

(C) Data Terkumpul (dengan Selang Kelas)

Varians, σ^{2} = \frac{\sum f x^{2}}{\sum f} - {\bar{x}}^{2}

Sisihan piawai, σ = \sqrt{varians}

Contoh 3:

Hitung min gaji harian dan sisihan piawai.

Penyelesaian:

Gaji harian (RM)	Bilangan pekerja, f	Nilai tengah, x	fx	fx²
10 – 14	40	12	480	5760
15 – 19	25	17	425	7225
20 – 24	15	22	330	7260
25 – 29	12	27	324	8748
30 – 34	8	32	256	8192
Total	100		1815	37185

\begin{array}{l} Min \bar{x} = \frac{\sum f x}{\sum f} \\ Min gaji harian = \frac{1815}{100} = 18.15 \end{array}

\begin{array}{l} Varians, σ^{2} = \frac{\sum f x^{2}}{\sum f} - {\bar{x}}^{2} \\ Sisihan piawai, σ = \sqrt{varians} \\ σ^{2} = \frac{37185}{100} - {18.15}^{2} \\ σ^{2} = 42.43 \\ σ = \sqrt{42.43} \\ σ = 6 .514 \end{array}

Bab 7 Statistik

Posted on May 30, 2016 by user

7.2 Sukatan Serakan (Bahagian 2)

7.2b Julat antara Kuartil 2

(C) Julat antara Kuartil untuk Data Terkumpul (dengan Selang Kelas)

Julat antara kuartil bagi data terkumpul boleh ditentukan melalui

Kaedah 1 (guna jadual kekerapan longgokan) atau Kaedah 2 (ogif).

\begin{array}{l} Kuartil pertama, k_{1} = L_{1} + (\frac{\frac{1}{4} N - F_{1}}{f_{k_{1}}}) C \\ Kuartil ketiga, k_{3} = L_{3} + (\frac{\frac{3}{4} N - F_{3}}{f_{k_{3}}}) C \end{array}

*Rumus-rumus ini diubahsuai daripada rumus median.

Contoh 1:

Jadual yang berikut menunjukkan taburan markah yang diperoleh sekumpulan pelajar tingkatan 4 dalam satu ujian matematik.

Anggarkan julat antara kuartil.

Penyelesaian:

Kaedah 1: Melalui Jadual Kekerapan Longgokan

Langkah 1:

Kuartil pertama, k₁= cerapan ke- ¼ (60)

= cerapan ke-15

Kuartil ketiga, k₃= cerapan ke- ¾ (60)

= cerapan ke- 45

Langkah 2:

\begin{array}{l} Kuartil pertama, k_{1} = L_{1} + (\frac{\frac{1}{4} N - F_{1}}{f_{k_{1}}}) C \\ = 39.5 + (\frac{15 - 12}{20}) 10 \\ = 39.5 + 1.5 \\ = 41 \end{array}

Langkah 3:

\begin{array}{l} Kuartil ketiga, k_{3} = L_{3} + (\frac{\frac{3}{4} N - F_{3}}{f_{k_{3}}}) C \\ = 49.5 + (\frac{45 - 32}{16}) 10 \\ = 49.5 + 8.125 \\ = 57.625 \end{array}

Langkah 4:

Julat antara kuartil

= kuartil ketiga – Kuartil pertama

= k₃– k₁

= 57.625 – 41

= 16.625

Bab 7 Statistik

Posted on May 30, 2016 by user

7.2 Sukatan Serakan (Bahagian 2)

7.2b Julat antara Kuartil 1

(A) Julat antara Kuartil untuk Data Tak Terkumpul

Contoh 1:

Cari julat antara kuartil bagi setiap set data yang berikut.

(a) 7, 5, 1, 3, 6, 11, 8

(b) 12, 4, 6, 18, 9, 16, 2, 14

Penyelesaian:

(a)

Susun semula data mengikut tertib menaik.

Julat antara kuartil

= kuartil ketiga – Kuartil pertama

= 8 – 3

= 5

(b)

Julat antara kuartil

= kuartil ketiga – Kuartil pertama

= \frac{14 + 16}{2} - \frac{4 + 6}{2}

= 15 – 5

= 10

(B) Julat antara Kuartil untuk Data Terkumpul (tanpa Selang Kelas)

Contoh 2:

Jadual yang berikut menunjukkan taburan markah yang diperoleh sekumpulan pelajar tingkatan 4 dalam satu ujian sains.

Tentukan julat antara kuartil bagi taburan itu.

Penyelesaian:

Kuartil pertama, k₁= cerapan ke- ¼ (24)

= cerapan ke- 6

= 2

Kuartil ketiga, k₃= cerapan ke- ¾ (24)

= cerapan ke- 18

= 4

Markah	kekerapan	Kekerapan longgokan
1	4	4
2	7	11 (k₁ terletak di sini)
3	5	16
4	2	18 (k₃ terletak di sini)
5	6	24

Julat antara kuartil

= kuartil ketiga – Kuartil pertama

= k₃ – k₁

= 4 – 2

= 2

Bab 7 Statistik

Posted on May 30, 2016 by user

7.2 Sukatan Serakan (Bahagian 1)

7.2a Julat

(A) Julat untuk Data Tak Terkumpul

Julat

= nilai cerapan terbesar – nilai cerapan terkecil

Contoh 1:

Cari julat bagi set data 2, 4, 7, 10, 13, 16 dan 18.

Penyelesaian:

Julat = nilai cerapan terbesar – nilai cerapan terkecil

= 18 – 2

= 16

(B) Julat untuk Data Terkumpul (dengan Selang Kelas)

Julat

= nilai tengah kelas tertinggi – nilai tengah kelas terendah

Contoh 2:

Jadual yang berikut menunjukkan taburan kekerapan skor yang diperoleh 100 pelajar dalam
suatu pertandingan.

Cari julat bagi set data.

Penyelesaian:

\begin{array}{l} J u l a t = nilai tengah kelas - nilai tengah kelas \\ tertinggi                   terendah \\ J u l a t = \frac{35 + 39}{2} - \frac{5 + 9}{2} \\ = 37 - 7 \\ = 30 \end{array}

Bab 7 Statistik

Posted on May 30, 2016 by user

7.1b Mod

Mod ialah cerapan yang mempunyai kekerapan paling tinggi dalam suatu set.

Contoh 1:

Cari mod bagi setiap set data yang berikut.

(a) 15, 18, 21, 25, 20, 18

(b) 3, 6, 9, 11, 17

Penyelesaian:

(a) Mod ialah 18. ← (18 berulang sebanyak 2 kali)

(b) Tiada mod.

(c) Mod ialah 1 dan 2. ← (kedua-dua nombor berulang 4 kali)

Bab 7 Statistik

Posted on May 30, 2016 by user

7.1a Min

Min = \frac{Hasil tambah nilai data}{Bilangan data}

(A) Data Tak Terkumpul

Contoh 1:

(a) Cari min bagi set data 2, 4, 7, 10, 13, 16 dan 18.

(b) Apabila suatu nilai x ditambah ke dalam set data di (a), nilai baru min menjadi 9.5. Tentukan nilai x.

Penyelesaian:

(a)

\begin{array}{l} \bar{x} = \frac{2 + 4 + 7 + 10 + 13 + 16 + 18}{7} \\ \bar{x} = \frac{70}{7} = 10 \end{array}

(b)

\begin{array}{l} Min baru = 9.5 \\ \frac{70 + x}{8} = 9.5 \\ 70 + x = 76 \\ x = 6 \end{array}

(B) Data Terkumpul (tanpa Selang Kelas)

Contoh 2:

Jadual kekerapan yang berikut menunjukkan markah ujian biologi bagi 40 orang pelajar.

Kira min markah.

Penyelesaian:

\begin{array}{l} Min markah, \bar{x} \\ \bar{x} = \frac{(50) (6) + (55) (8) + (60) (15) + (65) (10) + (70) (1)}{6 + 8 + 15 + 10 + 1} \\ \bar{x} = \frac{2360}{40} = 59 \end{array}

(C) Data Terkumpul (dengan Selang Kelas)

Contoh 3:

Jadual yang berikut menunjukkan taburan kekerapan skor yang diperoleh 100 pelajar dalam
suatu pertandingan.

Kira min skor.

Penyelesaian:

\begin{array}{l} Nilai tengah = \frac{5 + 9}{2} = 7 \\ Min skor, \bar{x} = \frac{\sum f x}{\sum f} = \frac{2290}{100} = 22.9 \end{array}