Question 1:
Rahman bought a house at RM180 000. The market price of the house increases by 15 % per year. After a year, Rahman sold his house at the price of RM 205 000.
Is the selling price higher compared to the market price? Show your working.
Solution:
Question 2:
A company makes a profit of RM 50 000 in year 2016. The projection of profit increase is fixed at 20 % from the previous year.
Predict the company profit in year 2018.
Solution:
Question 3:
Sharon wants to buy a new car with the price of RM 78 500. Her father gives her some money, which is 30 % of the car price. The deposit for the car is
of the price.
Would her father’s contribution be enough for her deposit? Give your reason with calculation.
Solution:
Question 4:
The profit of Company P and Company Q in March are RM38 000 and RM48 000 respectively. In April, the profit of Company P has increased by 20%.
Given the profit for both companies are equal in April, find the percentages decrease in profit of Company Q.
Solution:
Question 5:
A biscuit making company needs 200 tonnes of flour every month. Factory K supplies 80 tonnes, while the rest is supplied by Factory M. In a particular month, Factory K faces a problem which forces it to reduce its output by 15%.
Find the total percentage of the flour output of Factory M in order to accommodate the requirement of the biscuit making company.
Solution:




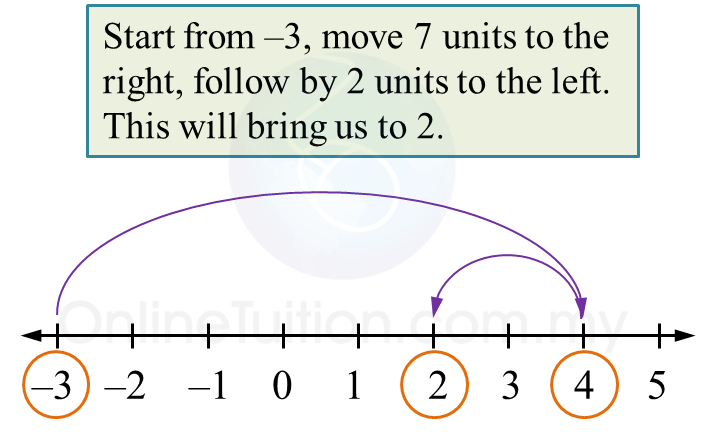

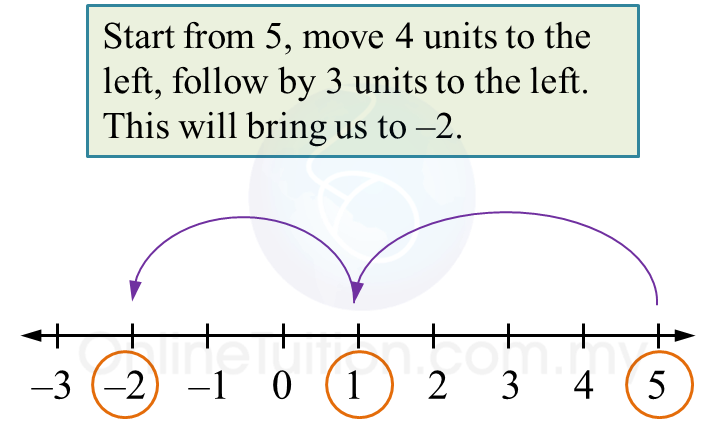


 Therefore,
Therefore, Therefore,
Therefore,

