15.2.1 Trigonometry, PT3 Focus Practice
Question 1:
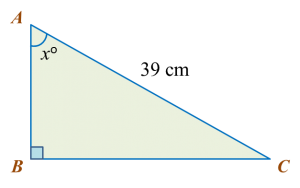
Diagram below shows a right-angled triangle ABC.
It is given that
, calculate the length, in cm, of AB.
Solution:
Question 2:
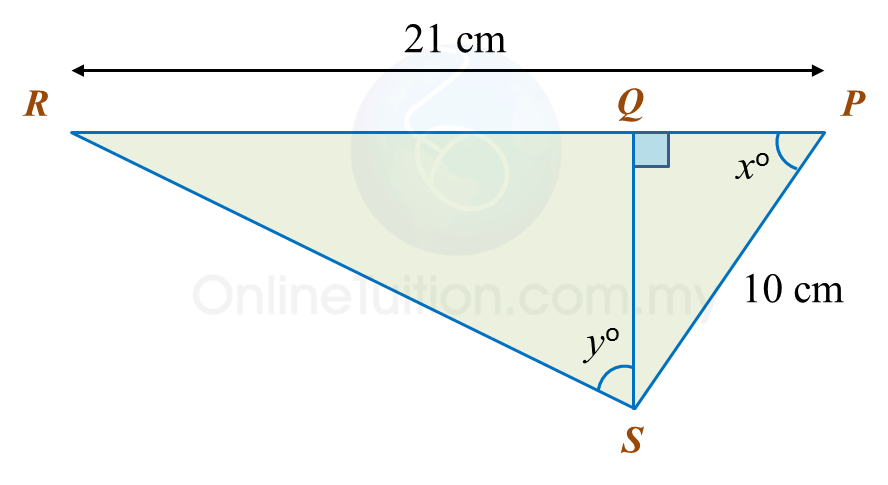
In the diagram, PQR and QTS are straight lines.
It is given that
, calculate the length, in cm, of RS.
Solution:
Question 3:
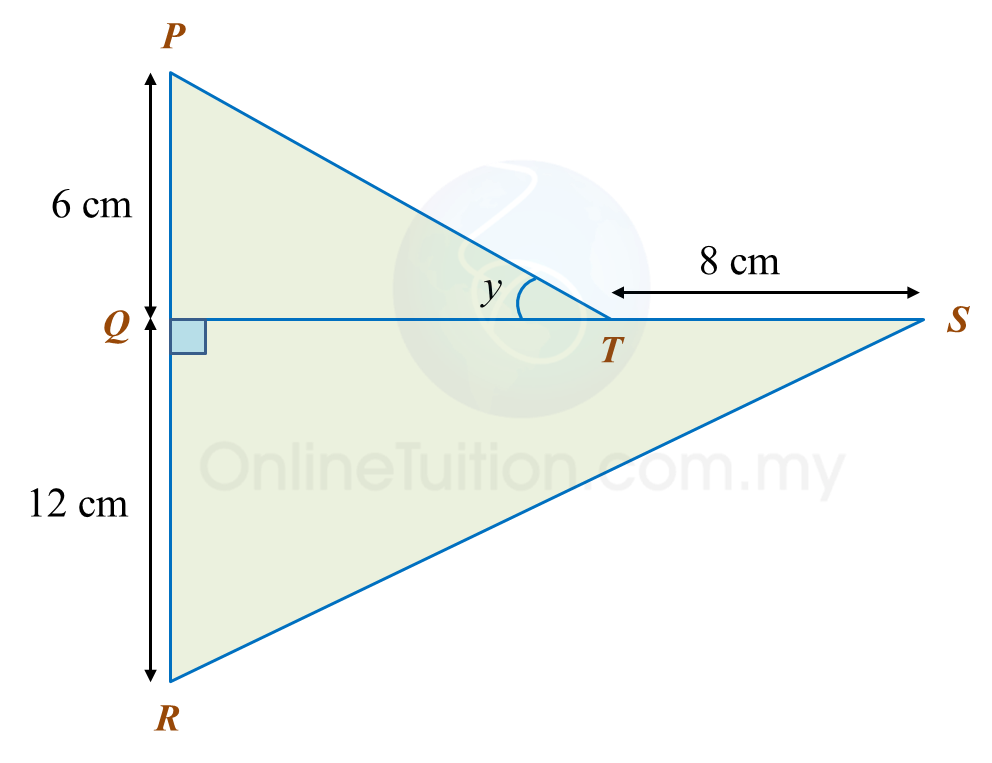
In the diagram, PQR is a straight line.
It is given that
, hence sin yo =
Solution:
Question 4:
Diagram below consists of two right-angled triangles.
Determine the value of cos xo.
Solution:
Question 5:
Diagram below consists of two right-angled triangles ABE and DBC.
ABC and EBD are straight lines.
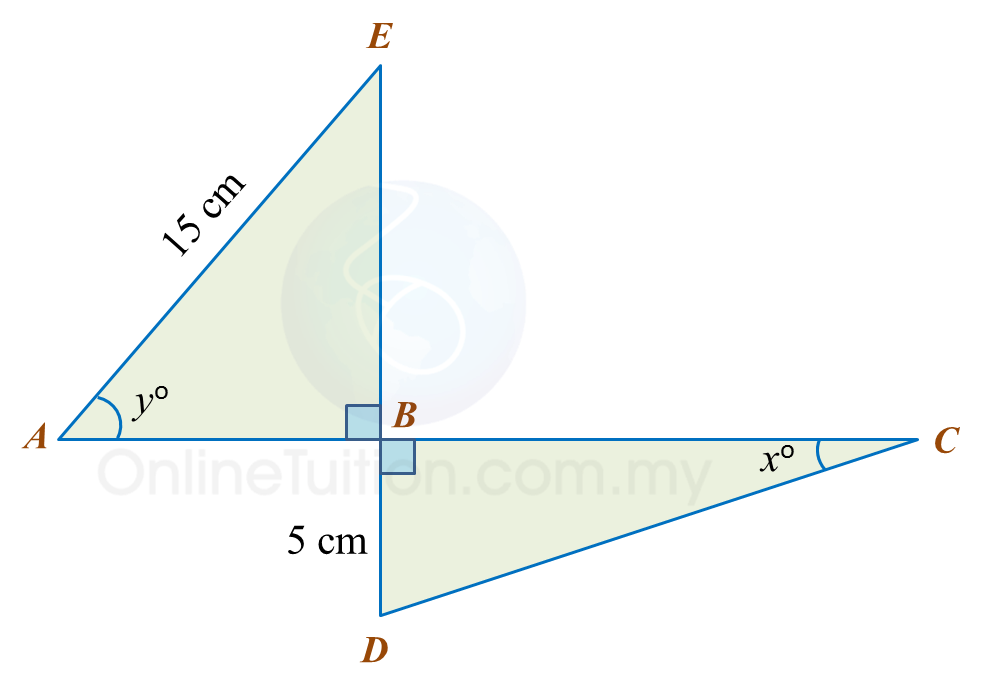
It is given that
Solution:
(a)
(b)
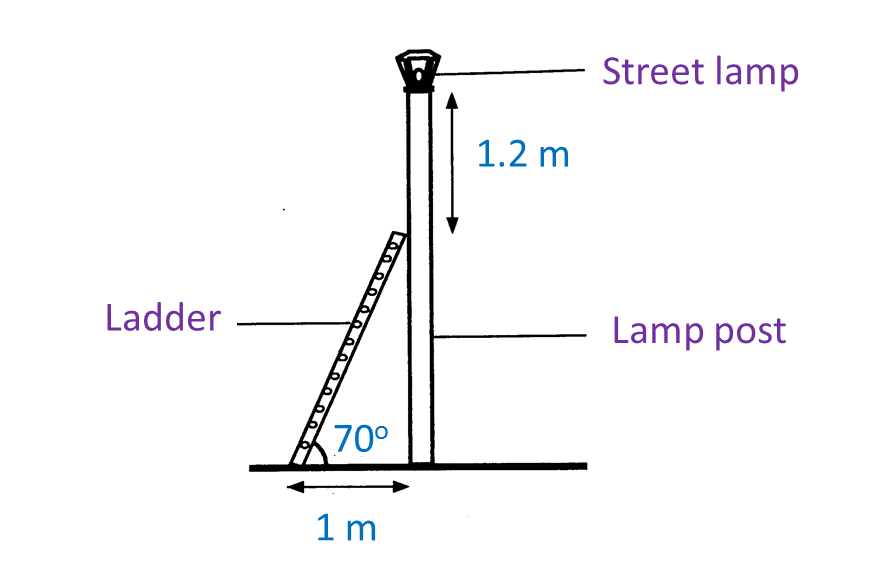 (a) What is the length, in m, of the ladder?
(a) What is the length, in m, of the ladder?
 (a) What is the length, in m, of the ladder?
(a) What is the length, in m, of the ladder?
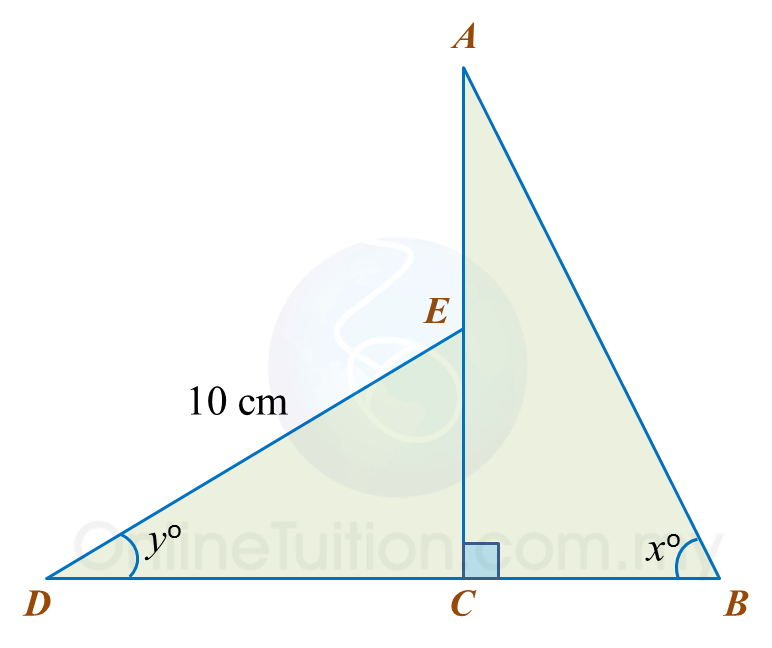

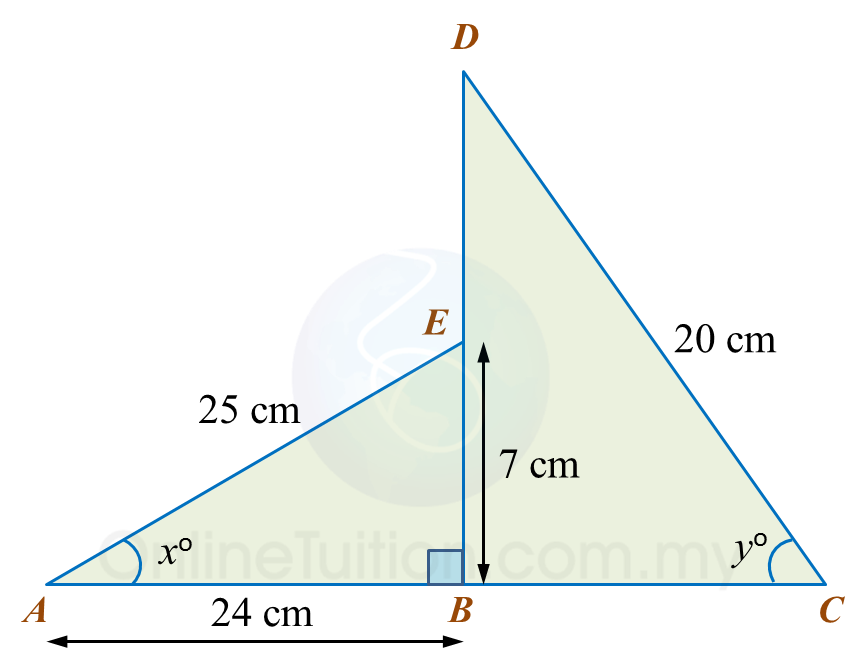
 Calculate
Calculate