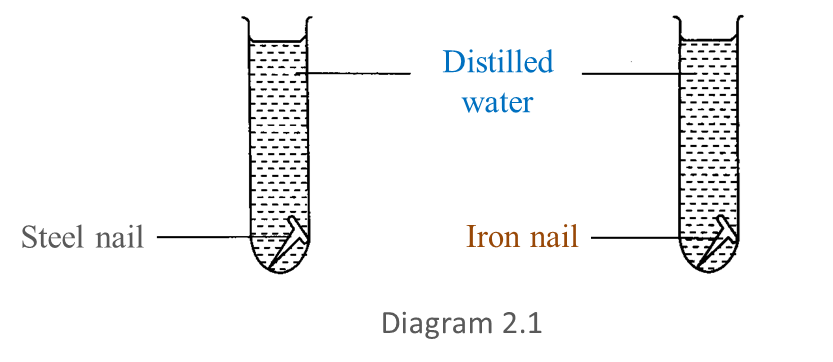
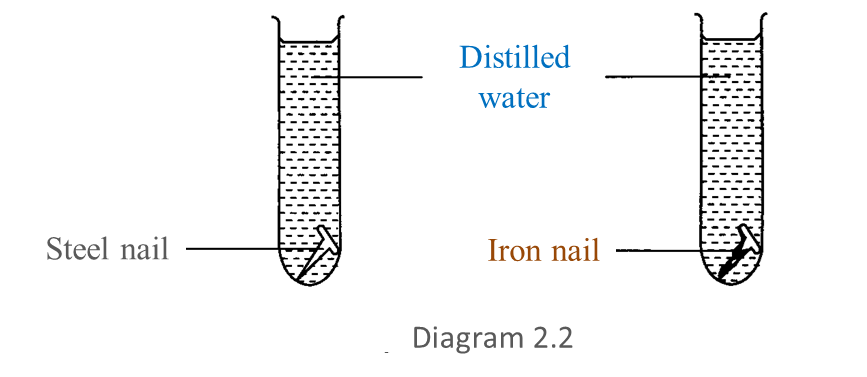
Solving Equation of Index Number
Example
Derive the equation $$y = {x^2} + \frac{3}{x}$$ by using first principle.
$$\eqalign{
& y = {x^2} + \frac{3}{x} \cr
& \frac{{dy}}{{dx}} = \mathop {\lim }\limits_{\delta x \to 0} \frac{{\delta y}}{{\delta x}} \cr
& = \mathop {\lim }\limits_{\delta x \to 0} \frac{{\left( {y + \delta y} \right) – y}}{{\delta x}} \cr
& = \mathop {\lim }\limits_{\delta x \to 0} \frac{{\left[ {{{\left( {x + \delta x} \right)}^2} + \frac{3}{{x + \delta x}}} \right] – \left[ {{x^2} + \frac{3}{x}} \right]}}{{\delta x}} \cr
& = \mathop {\lim }\limits_{\delta x \to 0} \frac{{{x^2} + 2x\delta x + \delta {x^2} – {x^2} + \frac{3}{{x + \delta x}} – \frac{3}{x}}}{{\delta x}} \cr
& = \mathop {\lim }\limits_{\delta x \to 0} \frac{{2x\delta x + \delta {x^2}}}{{\delta x}} + \frac{{\frac{{3x – 3(x + \delta x)}}{{x(x + \delta x)}}}}{{\delta x}} \cr
& = \mathop {\lim }\limits_{\delta x \to 0} 2x + \delta x + \frac{{ -3 \delta x}}{{x(x + \delta x)}} \times \frac{1}{{\delta x}} \cr
& = \mathop {\lim }\limits_{\delta x \to 0} 2x + \delta x + \frac{{ – 3}}{{x(x + \delta x)}} \cr
& = 2x – \frac{3}{{{x^2}}} \cr} $$
$$\frac{{dy}}{{dx}} = \mathop {\lim }\limits_{\delta x \to 0} \frac{{\delta y}}{{\delta x}}$$
 (Speed is derived from dividing distance by time.)
(Speed is derived from dividing distance by time.)












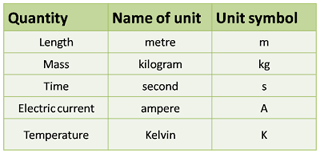 TIPS: In SPM, you MUST remember all 5 base quantities and its SI unit.
TIPS: In SPM, you MUST remember all 5 base quantities and its SI unit. 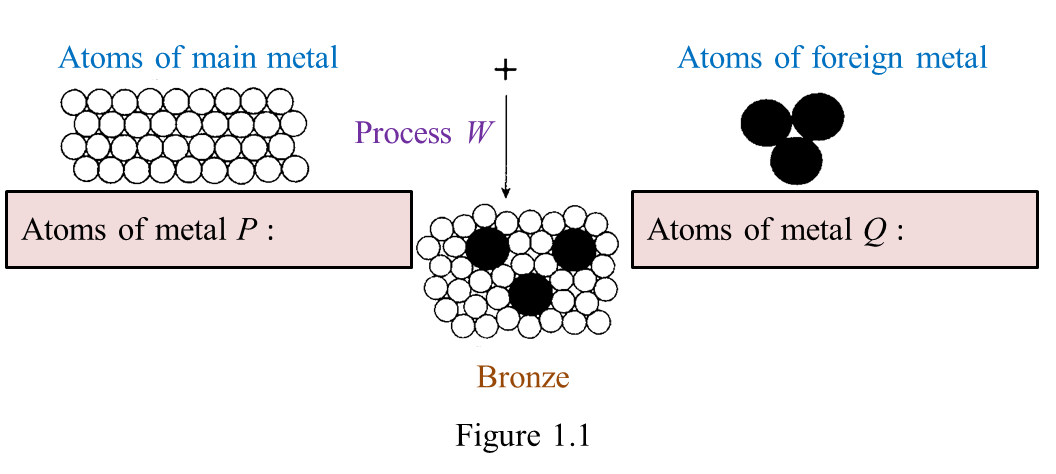
 (d) The medal in Figure 1.2 is made of bronze.
(d) The medal in Figure 1.2 is made of bronze.