2.4.3 The Nitrogen Cycle and Its Importance (Structured Questions)

Posted on April 20, 2017 by user

Question 1:
Diagram 1 shows part of nitrogen cycle.

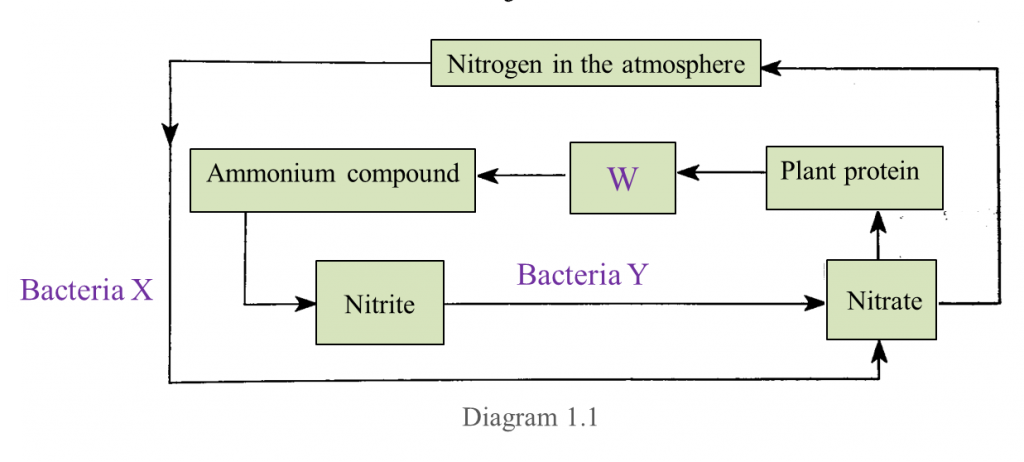
(a) What is represented by W? [1 mark]

(b) Name bacteria X and bacteria Y. [2 marks]

(c) State one importance of the nitrogen cycle in Diagram 1.1. [1 mark]

(d) Bacteria X can be found in the root nodules of a plant as shown in Diagram 1.2.[1 mark]

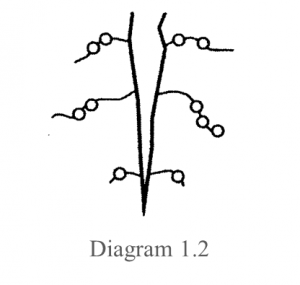
Name the type of plant shown in Diagram 1.2.
(e) The nitrogen cycle consists of several processes.
In Table below, mark (\/) the process involved in the nitrogen cycle. [1 mark]

Answer:
(a) Animal proteins

(b)
X: Nitrogen-fixing bacteria
Y: Nitrifying bacteria

(c)
1. Ensures that nitrogen and compounds of nitrogen are always present around us.
2. Maintains relatively steady levels of nitrogen and compounds of nitrogen around us.
(any one)

(d) Leguminous plant, pea plant, beans (any one)

(e)

8.2.3 Basic Measurements, PT3 Practice

Posted on April 7, 2017 by user

Question 11:
George departed for Kuantan from Kuala Lumpur at 9.30 a.m. He stopped at a rest station for 45 minutes. Then, he continued his journey and arrived at his destination at 3.45 p.m. How long did he travel on the road.

Solution:
Time taken on the road
= (1545 – 0930) – 0045 ← [3.45 p.m. change to 24-hour system = 1545 (1200 + 0345)]
= 0615 – 0045
= 0530
= 5 hours 30 minutes

Question 12:
Rita began doing her homework at 8.25 in the morning. She took a break for 45 minutes to have some exercises and ½ hour to have lunch. If she finished her homework at 4.45 in the evening on the same day, how long did she take to do her homework?

Solution:
Time taken for Rita to finish her homework
= (1645 – 0825) – (0030 + 0045) ← [4.45 p.m. = 1645 (1200 + 0445)]
= 0820 – 0115
= 0705
= 7 hours 5 minutes

Question 13:
Roslan attended a tuition class for 2½ hours. The class started at 7.15 p.m. The class finished 35 minutes earlier due to power failure.
At what time did the class finish?

Solution:
Class finish at
= (1915 + 0230) – 0035 ← [7.15 p.m. = 1915 (1200 + 0715)]
= 2145 – 0035
= 2110 → (9.10 p.m.)

Question 14:
An aeroplane took off from Kuala Lumpur to Singapore at 2.45 p.m. The flight normally takes 55 minutes. The aeroplane was delayed and landed at Singapore at 4.50 p.m.
How long, in minutes, was the aeroplane delayed?

Solution:
Expected arrival time
= 2.45 p.m. + 55 minutes
= 3.40 p.m.

Time delayed
= 4.50 p.m. – 3.40 p.m.
= 1 hour 10 minutes
= 70 minutes

Question 15:
The flight from Kuala Lumpur to Kota Kinabalu takes 1 hour 45 minutes.
Jacky’s flight should leave at 2.15 p.m. but is delayed by 50 minutes.
At what time, in the 24-hour system, he will reach Kota Kinabalu?

Solution:
2.15 p.m. = 1415 hours
Actual departure time
= 1415 hours + 50 minutes
= 1505 hours

Arrival time at Kota Kinabalu
= 1505 + 0145
= 1650

8.2.2 Basic Measurements, PT3 Practice

Posted on April 5, 2017 by user

Question 6:
The mass of a box containing 6 papayas is 21.32 kg. The mass of the box when it is empty is 1.46 kg.
Calculate the average mass, in g, of a papaya.

Solution:
Mass of 6 papayas
= 21.32 – 1.46
= 19.86 kg

Average mass of a papaya
= 19.86 ÷ 6
= 3.31 kg
= 3.31 × 1000 g
= 3310 g

Question 7:
Louis bought 600 g of cookies. Dennis bought twice the mass of cookies that Jackson bought. They bought 1.35 kg of cookies altogether. Calculate the mass, in g, of cookies bought by Jackson.

Solution:
Let Jackson bought w g of cookies.
600 g + 2 × w + w = 1.35 kg
600 g + 3w = 1.35 kg
600 g + 3w = 1350 g
3w = 1350 g – 600 g
w = 750 g ÷ 3
w = 250 g

Question 8:
If the mass of 4 packets of candies is 2.6 kg, what is the mass of 9 packets of the same candies, in kg?

Solution:

\begin{array}{l} Mass of 4 packets of candies = 2 .6 kg \\ Mass of 9 packets of candies = \frac{2.6}{4} \times 9 \\ = 5.85 kg \end{array}

Question 9:
It is given that

\frac{1}{4}

of fruits is supplied to Juice Stall A and

\frac{2}{7}

to Juice Stall B. The remaining 133.25 kg is sold to a fruit stall.
Calculate the mass of fruits that has been supplied to Fruit Stall B.

Solution:

\begin{array}{l} \frac{1}{4} + \frac{2}{7} = \frac{7}{28} + \frac{8}{28} \\ = \frac{15}{28} \\ Remaining fruits sold to fruit stall \\ = 1 - \frac{15}{28} \\ = \frac{13}{28} \\ Total mass of fruits \\ = \frac{28}{13} \times 133.25 \\ = 287 kg \\ Mass of fruits supplied to Juice Stall B \\ = \frac{2}{7} \times 287 \\ = 82 kg \end{array}

Question 10:
The mixture of metal to produce a piece of 50 sen coin are

\frac{2}{3} zinc, \frac{1}{5} nickel

and the rest is copper.
If the mass of copper is 1.6 g, find the total mass, in g, of zinc and nickel.

Solution:

\begin{array}{l} Fraction of copper \\ = 1 - \frac{2}{3} - \frac{1}{5} \\ = \frac{15}{15} - \frac{10}{15} - \frac{3}{15} \\ = \frac{2}{15} \\ Portion of copper = 2 g \\ Portion of zinc and nickel = 13 g \\ 2 \leftrightarrow 1.6 g \\ Total mass of zinc and nickel, \\ 13 \leftrightarrow \frac{13 \times 1.6}{2} = 10.4 g \end{array}

8.2.1 Basic Measurements, PT3 Practice

Posted on April 1, 2017 by user

[adinserter name="Block 3"]

Question 1:
Karen has 18 m of ribbon to tie 16 bars of chocolate and 28 boxes of sweets. A bar of chocolate needs 24 cm of ribbon and a box of sweets needs 38 cm of ribbon.
Calculate the length, in m, of the remaining ribbon.

Solution:
Length of ribbon needed
= (16 × 24 cm) + (28 × 38 cm)
= 384 cm + 1064 cm
= 1448 cm
= 14.48 m

Length of remaining ribbon
= 18 m – 14.48 m
= 3.52 m

[adinserter name="Block 3"]

Question 2:
The length of a red string is 4 m 80 cm. The length of a brown string is ⅔ of the length of the red string. The length of a black string is twice the length of the brown string.
Calculate the total length, in m, of the brown and the black strings.

Solution:

\begin{array}{l} Length of brown string \\ = \frac{2}{3} \times 4 m 80 cm \\ = \frac{2}{3} \times 4.8 \\ = 3.2 m \\ Length of black string \\ = 2 \times 3.2 m \\ = 6.4 m \\ Total length = 3.2 m + 6.4 m \\ = 9.6 m \end{array}

[adinserter name="Block 3"]

Question 3:
Kelly has 13 m of cloth. She uses it to make 6 curtains and 4 tablecloths. Each curtain requires 1.25 m of cloth and each tablecloth requires 90 cm of cloth.
What is the length, in m, of the remaining cloth?

Solution:
Length of cloth used to make curtains
= 6 × 1.25 m
= 7.5 m

Length of cloth used to make tablecloth
= 4 × 90 cm
= 360 cm
= 3.6 m

Length of the remaining cloth
= 13 – 7.5 – 3.6
= 1.9 m

[adinserter name="Block 3"]

Question 4:
A rope measuring 6 m 30 cm is cut into 1.6 m, 96 cm and the remainder into two equal parts. Find the length of each of the remaining parts, in cm.

Solution:
(6 m 30 cm – 1.6 m – 96 cm) ÷ 2
= (630 cm – 160 cm – 96 cm) ÷ 2
= 374 cm ÷ 2
= 187 cm