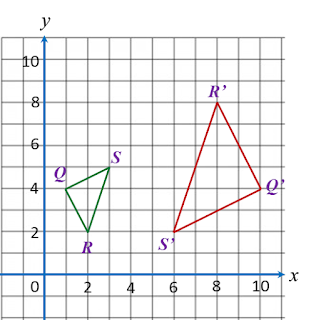
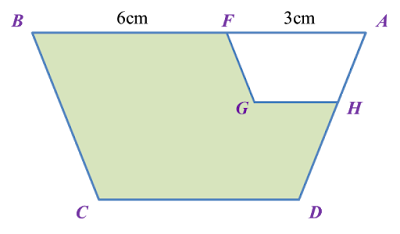
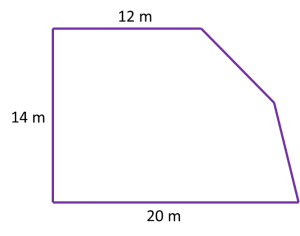
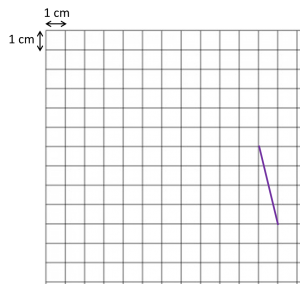
Question 6:
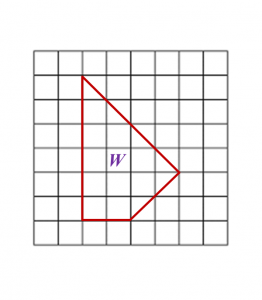
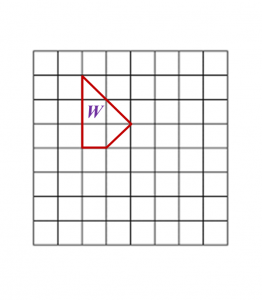
Diagram below shows a ‘Wayang Kulit’ performed by Tok Dalang. The height of the screen use is 1.5 m. The shadow on the screen is ⅔ the height of the screen.
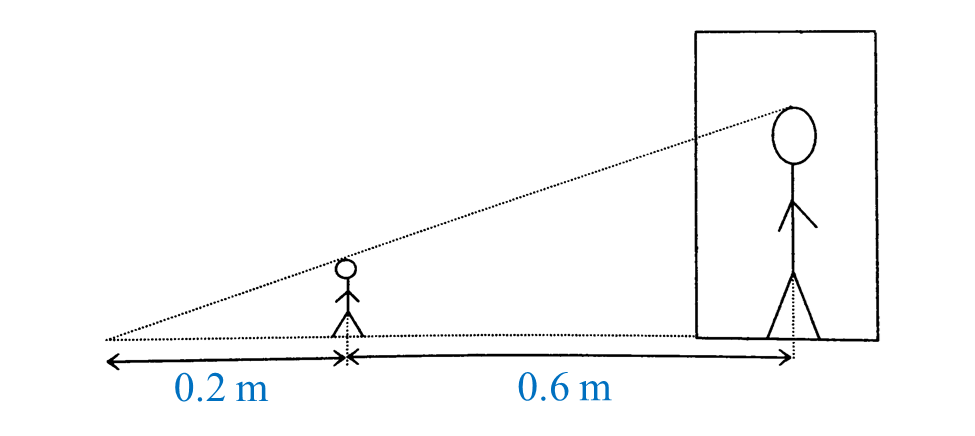 What is the height, in cm, of the puppet used by Tok Dalang?
What is the height, in cm, of the puppet used by Tok Dalang?
Solution:
Diagram below shows a ‘Wayang Kulit’ performed by Tok Dalang. The height of the screen use is 1.5 m. The shadow on the screen is ⅔ the height of the screen.
 What is the height, in cm, of the puppet used by Tok Dalang?
What is the height, in cm, of the puppet used by Tok Dalang?Solution:
Question 7:
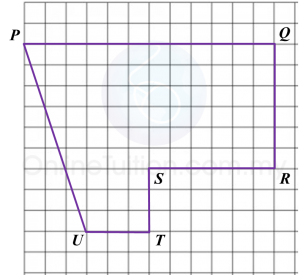
Diagram below shows the shadow of a pillar form on the wall from the light of a spotlight.
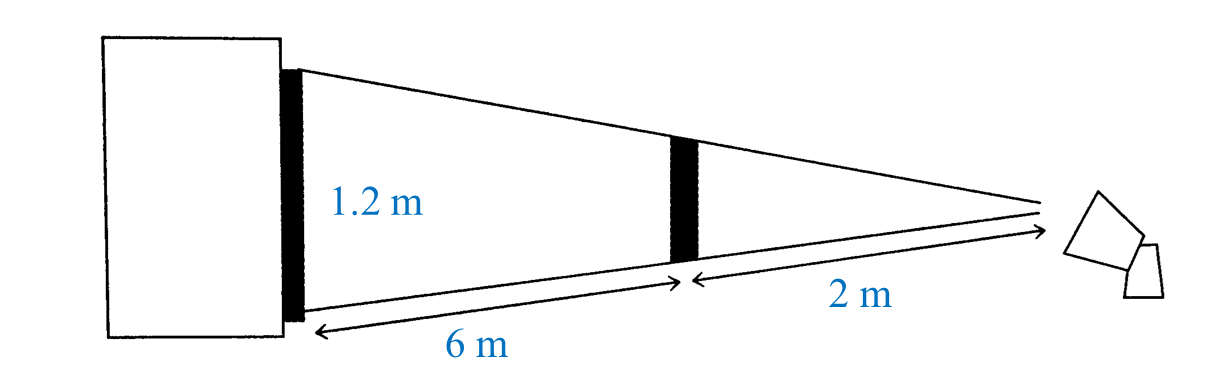 (a) State the scale factor of the enlargement.
(a) State the scale factor of the enlargement.
(b) Find the height of the pillar.
Solution:
(a)
(b)
Diagram below shows the shadow of a pillar form on the wall from the light of a spotlight.
 (a) State the scale factor of the enlargement.
(a) State the scale factor of the enlargement.(b) Find the height of the pillar.
Solution:
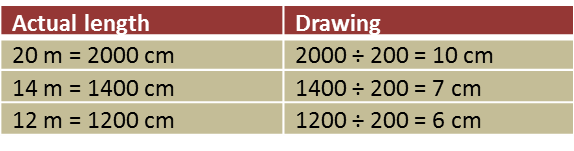
(a)
(b)
Question 8:
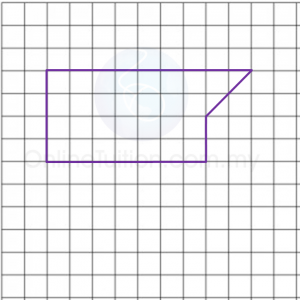
In diagram below, a torch light is used to form a shadow of a candle on the screen.
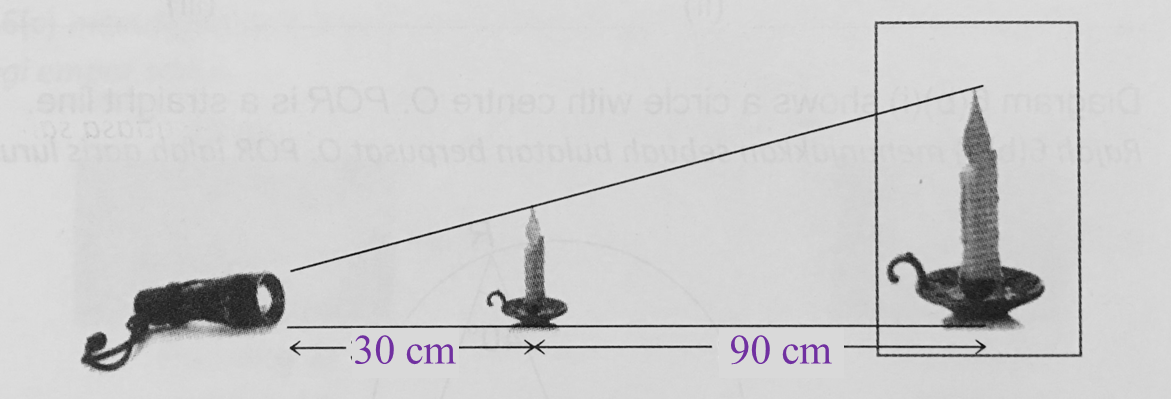
The height of the candle is 15 cm.
If the height of the shadow of the candle is ¾ of the height of the screen, find the height of the screen.
Solution:
In diagram below, a torch light is used to form a shadow of a candle on the screen.

The height of the candle is 15 cm.
If the height of the shadow of the candle is ¾ of the height of the screen, find the height of the screen.
Solution: