3.7 Fungsi Kuadratik, SPM Praktis (Soalan Panjang)
Soalan 3:
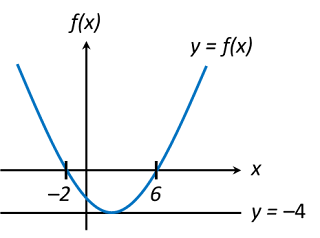
Rajah di atas menunjukkan graf fungsi kuadratik y = f(x). Garis lurus y = –4 ialah tangen kepada lengkung y = f(x).
(a)
Tulis persamaan paksi simetri untuk fungsi f(x).
(b)
Ungkapakan f(x) dalam bentuk (x + p)2 + q , dengan keadaan p dan q ialah pemalar.
(c)
Cari julat nilai xsupaya
(i)
f(x) < 0, (ii) f(x) ≥ 0.
Penyelesaian:
(a)
Koordinat-x titik minimum = titik tengah bagi (–2, 0) dan (6, 0)
Maka, persamaan paksi simetri untuk fungsi f(x) ialah x = 2.
(b)
Gantikan x = 2 dalam x + p = 0,
2 + p = 0
p = –2
dan q = –4 (nilai f(x) yang paling kecil)
Maka, f(x) = (x + p)2 + q
f(x) = (x – 2)2 – 4
(c)(i) Daripada graf, bagi f(x) < 0, julat nilai x ialah –2 < x < 6 ← (bahagian graf di bawah paksi-x).
(c)(ii) Daripada graf, bagi f(x) ≥ 0, julat nilai x ialah x ≤ –2 atau x ≥ 6 ← (bahagian graf di atas paksi-x).
Soalan 4:
Penyelesaian:
(a)
Graf fungsi y = (k – 2)(k – 10) memotong paksi ufuk di k = 2 dan k = 10.
Graf melekung ke bawah untuk b2 – 4ac < 0.

Julat nilai k yang memuaskan ketaksamaan di atas ialah 2 < k < 10.
(b)
Nilai minimum bagi (h + 1) + 8 ialah 8, satu nilai positif. Oleh itu, b2 – 4ac > 0 untuk semua nilai h.
Maka, punca-punca persamaan kuadratik hx2 – (h + 3)x + 1 = 0 adalah nyata dan berbeza untuk semua nilai h.
- Cari julat nilai k supaya persamaan x2 – kx + 3k – 5 = 0 tidak mempunyai punca.
- Buktikan bahawa punca-punca persamaan kuadratik hx2 – (h + 3)x + 1 = 0 adalah nyata dan berbeza untuk semua nilai h.
Penyelesaian:
(a)
Graf fungsi y = (k – 2)(k – 10) memotong paksi ufuk di k = 2 dan k = 10.
Graf melekung ke bawah untuk b2 – 4ac < 0.

Julat nilai k yang memuaskan ketaksamaan di atas ialah 2 < k < 10.
(b)
Nilai minimum bagi (h + 1) + 8 ialah 8, satu nilai positif. Oleh itu, b2 – 4ac > 0 untuk semua nilai h.
Maka, punca-punca persamaan kuadratik hx2 – (h + 3)x + 1 = 0 adalah nyata dan berbeza untuk semua nilai h.