Long Question 9

Posted on May 17, 2020 by Myhometuition

Question 9 (10 marks):
Diagram shows the straight line 4y = x – 2 touches the curve x = y² + 6 at point P.

Find
(a) the coordinates of P,
(b) the area of the shaded region,
(c) the volume of revolution, in terms of π, when the region bounded by the curve and the straight line x = 8 is revolved through 180^o about the x-axis.

Solution:
(a)

\begin{array}{l} 4 y = x - 2......... (1) \\ x = y^{2} + 6......... (2) \\ Substitute (2) into (1): \\ 4 y = (y^{2} + 6) - 2 \\ y^{2} - 4 y + 4 = 0 \\ (y - 2) (y - 2) = 0 \\ y - 2 = 0 \\ y = 2 \\ Substitute y = 2 into (2): \\ x = {(2)}^{2} + 6 \\ x = 10 \\ Thus, P = (10, 2) . \end{array}

(b)

\begin{array}{l} At x-axis, y = 0 \\ ∴ 4 y = x - 2 \\ 0 = x - 2 \\ x = 2 \\ Area of shaded region \\ = Area of triangle - Area under the curve \\ = \frac{1}{2} (10 - 2) (2) - \int_{6}^{10} y d x \\ = 8 - \int_{6}^{10} \sqrt{x - 6} d x \leftarrow \begin{array}{l} x = y^{2} + 6 \\ y = \sqrt{x - 6} \end{array} \\ = 8 - \int_{6}^{10} {(x - 6)}^{\frac{1}{2}} d x \\ = 8 - {[\frac{{(x - 6)}^{\frac{1}{2} + 1}}{\frac{1}{2} + 1}]}_{6}^{10} \\ = 8 - {[\frac{2 {(x - 6)}^{\frac{3}{2}}}{3}]}_{6}^{10} \\ = 8 - [\frac{2 {(10 - 6)}^{\frac{3}{2}}}{3} - \frac{2 {(6 - 6)}^{\frac{3}{2}}}{3}] \\ = 8 - \frac{16}{3} \\ = \frac{8}{3} {units}^{2} \end{array}

(c)

\begin{array}{l} Volume of revolution \\ = π \int_{6}^{8} y^{2} d x \\ = π \int_{6}^{8} (x - 6) d x \leftarrow \begin{array}{l} x = y^{2} + 6 \\ y^{2} = x - 6 \end{array} \\ = π {[\frac{x^{2}}{2} - 6 x]}_{6}^{8} \\ = π [(32 - 48) - (18 - 36)] \\ = 2 π {units}^{3} \end{array}

SPM Practice 3 (Linear Law) – Question 3

Posted on May 17, 2020 by Myhometuition

Question 3
The table below shows the corresponding values of two variables, x and y, that are related by the equation

y = 5 h x^{2} + \frac{k}{h} x

, where h and k are constants.

(a) Using a scale of 2 cm to 1 unit on the x - axis and 2 cm to 0.2 units on the

\frac{y}{x}

– axis, plot the graph of

\frac{y}{x}

against x . Hence, draw the line of best fit.

(b) Use your graph in (a) to find the values of
(i) h,
(ii) k,
(iii) y when x = 6.

Solution
Step 1 : Construct a table consisting X and Y.

Step 2 : Plot a graph of Y against X, using the scale given and draw a line of best fit

Steps to draw line of best fit - Click here

Step 3 : Calculate the gradient, m, and the Y-intercept, c, from the graph

Step 4 : Rewrite the original equation given and reduce it to linear form

Step 5 : Compare with the values of m and c obtained, find the values of the unknown required

(b) (iii) find the value of y when x = 6.

SPM Practice 3 (Linear Law) – Question 2

Posted on May 17, 2020 by Myhometuition

Question 2 (10 marks):
Use a graph to answer this question.
Table 1 shows the values of two variables, x and y, obtained from an experiment.
The variables x and y are related by the equation

y - \sqrt{h} = \frac{h k}{x}

, where h and k are constants.

(a) Plot xy against x, using a scale of 2 cm to 1 unit on the x-axis and 2 cm to 5 units on the xy-axis.
Hence, draw the line of best fit.

(b) Using the graph in 2(a), find
(i) the value of h and of k,
(ii) the correct value of y if one of the values of y has been wrongly recorded during the experiment.

Solution:
(a)

(b)

\begin{array}{l} y - \sqrt{h} = \frac{h k}{x} \\ x y - \sqrt{h} x = h k \\ x y = \sqrt{h} x + h k \\ Y = m X + C \\ Y = x y, m = \sqrt{h}, C = h k \end{array}

(b)(i)

\begin{array}{l} m = \frac{36.5}{5.1} \\ \sqrt{h} = \frac{36.5}{5.1} \\ \sqrt{h} = 7.157 \\ h = 51.22 \\ C = - 4 \\ h k = - 4 \\ k = \frac{- 4}{h} \\ k = - \frac{4}{51.22} \\ k = - 0.0781 \end{array}

(b)(ii)

\begin{array}{l} x y = 21 \\ 3.5 y = 21 \\ y = \frac{21}{3.5} = 6.0 \\ Correct value of y is 6 .0 . \end{array}

Long Question 10

Posted on May 17, 2020 by Myhometuition

Question 10 (10 marks):
Diagram shows a triangle ABC. The straight line AE intersects with the straight line BC at point D. Point V lies on the straight line AE.

\begin{array}{l} It is given that \vec{B D} = \frac{1}{3} \vec{B C}, \vec{A C} = 6 \underset{˜}{x} and \vec{A B} = 9 \underset{˜}{y} . \\ (a) Express in terms of \underset{˜}{x} and / or \underset{˜}{y} : \\ (i) \vec{B C}, \\ (i i) \vec{A D} . \\ (b) It is given that \vec{A V} = m \vec{A D} and \vec{B V} = n (\underset{˜}{x} - 9 \underset{˜}{y}), where m and n are constants . \\ Find the value of m and of n . \\ (c) Given \vec{A E} = h \underset{˜}{x} + 9 \underset{˜}{y}, where h is a constant, find the value of h . \end{array}

Solution:
(a)(i)

\begin{array}{l} \vec{B C} = \vec{B A} + \vec{A C} \\ = - 9 \underset{˜}{y} + 6 \underset{˜}{x} \\ = 6 \underset{˜}{x} - 9 \underset{˜}{y} \end{array}

(a)(ii)

\begin{array}{l} \vec{A D} = \vec{A B} + \vec{B D} \\ = 9 \underset{˜}{y} + \frac{1}{3} \vec{B C} \\ = 9 \underset{˜}{y} + \frac{1}{3} (6 \underset{˜}{x} - 9 \underset{˜}{y}) \\ = 9 \underset{˜}{y} + 2 \underset{˜}{x} - 3 \underset{˜}{y} \\ = 2 \underset{˜}{x} + 6 \underset{˜}{y} \end{array}

(b)

\begin{array}{l} Given \vec{A V} = m \vec{A D} \\ = m (2 \underset{˜}{x} + 6 \underset{˜}{y}) \\ = 2 m \underset{˜}{x} + 6 m \underset{˜}{y} \\ \vec{A V} = \vec{A B} + \vec{B V} \\ = 9 \underset{˜}{y} + n (\underset{˜}{x} - 9 \underset{˜}{y}) \\ = 9 \underset{˜}{y} + n \underset{˜}{x} - 9 n \underset{˜}{y} \\ = n \underset{˜}{x} + (9 - 9 n) \underset{˜}{y} \\ By equating the coefficients of \underset{˜}{x} and \underset{˜}{y}, \\ 2 m \underset{˜}{x} + 6 m \underset{˜}{y} = n \underset{˜}{x} + (9 - 9 n) \underset{˜}{y} \\ 2 m = n \\ n = 2 m ............. (1) \\ 6 m = 9 - 9 n ............. (2) \\ Substitute (1) into (2), \\ 6 m = 9 - 9 (2 m) \\ 6 m = 9 - 18 m \\ 24 m = 9 \\ m = \frac{9}{24} = \frac{3}{8} \\ From (1) : \\ n = 2 (\frac{3}{8}) = \frac{3}{4} \end{array}

(c)

\begin{array}{l} A, D and E are collinear . \\ \vec{A D} = k (\vec{A E}) \\ \vec{A D} = k (h \underset{˜}{x} + 9 \underset{˜}{y}) \\ 2 \underset{˜}{x} + 6 \underset{˜}{y} = k h \underset{˜}{x} + 9 k \underset{˜}{y} \\ Equating the coefficients of \underset{˜}{y} : \\ 9 k = 6 \\ k = \frac{6}{9} \\ k = \frac{2}{3} \\ Equating the coefficients of \underset{˜}{x} : \\ k h = 2 \\ (\frac{2}{3}) h = 2 \\ h = 2 \times \frac{3}{2} \\ h = 3 \end{array}

Long Question 9

Posted on May 17, 2020 by Myhometuition

Question 9 (10 marks):
Diagram 5 shows triangles OAQ and OPB where point P lies on OA and point Q lies on OB. The straight lines AQ and PB intersect at point R.

\begin{array}{l} It is given that \vec{O A} = 18 \underset{˜}{x}, \vec{O B} = 16 \underset{˜}{y}, O P : P A = 1 : 2, O Q : Q B = 3 : 1, \\ \vec{P R} = m \vec{P B} and \vec{Q R} = n \vec{Q A}, where m and n are constants . \\ (a) Express \vec{O R} in terms of \\ (i) m, \underset{˜}{x} and \underset{˜}{y}, \\ (i i) n, \underset{˜}{x} and \underset{˜}{y}, \\ (b) Hence, find the value of m and of n . \\ (c) Given | \underset{˜}{x} | = 2 units, | \underset{˜}{y} | = 1 unit and O A is perpendicular to O B calculate | \vec{P R} | . \end{array}

Solution:
(a)(i)

\begin{array}{l} \vec{O R} = \vec{O P} + \vec{P R} \\ = \frac{1}{3} \vec{O A} + m \vec{P B} \\ = \frac{1}{3} (18 \underset{˜}{x}) + m (\vec{P O} + \vec{O B}) \\ = 6 \underset{˜}{x} + m (- 6 \underset{˜}{x} + 16 \underset{˜}{y}) \end{array}

(a)(ii)

\begin{array}{l} \vec{O R} = \vec{O Q} + \vec{Q R} \\ = \frac{3}{4} \vec{O B} + n \vec{Q A} \\ = \frac{3}{4} (16 \underset{˜}{y}) + n (\vec{Q O} + \vec{O A}) \\ = 12 \underset{˜}{y} + n (- 12 \underset{˜}{y} + 18 \underset{˜}{x}) \\ = (12 - 12 n) \underset{˜}{y} + 18 n \underset{˜}{x} \end{array}

(b)

\begin{array}{l} 6 \underset{˜}{x} + m (- 6 \underset{˜}{x} + 16 \underset{˜}{y}) = (12 - 12 n) \underset{˜}{y} + 18 n \underset{˜}{x} \\ 6 \underset{˜}{x} - 6 m \underset{˜}{x} + 16 m \underset{˜}{y} = 18 n \underset{˜}{x} + 12 \underset{˜}{y} - 12 n \underset{˜}{y} \\ by comparison; \\ 6 - 6 m = 18 n \\ 1 - m = 3 n \\ m = 1 - 3 n .............. (1) \\ 16 m = 12 - 12 n \\ 4 m = 3 - 3 n .............. (2) \\ Substitute (1) into (2), \\ 4 (1 - 3 n) = 3 - 3 n \\ 4 - 12 n = 3 - 3 n \\ 9 n = 1 \\ n = \frac{1}{9} \\ Substitute n = \frac{1}{9} into (1), \\ m = 1 - 3 (\frac{1}{9}) \\ m = \frac{2}{3} \end{array}

[adinserter block="3"]

(c)

\begin{array}{l} | \underset{˜}{x} | = 2, | \underset{˜}{y} | = 1 \\ \vec{P R} = \frac{2}{3} \vec{P B} \\ = \frac{2}{3} (- 6 \underset{˜}{x} + 16 \underset{˜}{y}) \\ = - 4 \underset{˜}{x} + \frac{32}{3} \underset{˜}{y} \\ | \vec{P R} | = \sqrt{{[- 4 (2)]}^{2} + {[\frac{32}{3} (1)]}^{2}} \\ = \sqrt{\frac{1600}{9}} \\ = \frac{40}{3} units \end{array}

Long Question (Question 10)

Posted on May 17, 2020 by Myhometuition

Question 10 (5 marks):
Solve the following simultaneous equations:
x – 3y = 1,
x²+ 3xy + 9y²= 7

Solution:

\begin{array}{l} x - 3 y = 1................... (1) \\ x^{2} + 3 x y + 9 y^{2} = 7................... (2) \\ From (1) : x = 3 y + 1................... (3) \\ Substitute (3) into (2) : \\ {(3 y + 1)}^{2} + 3 (3 y + 1) y + 9 y^{2} = 7 \\ 9 y^{2} + 6 y + 1 + 9 y^{2} + 3 y + 9 y^{2} - 7 = 0 \\ 27 y^{2} + 9 y - 6 = 0 \\ 9 y^{2} + 3 y - 2 = 0 \\ (3 y - 1) (3 y + 2) = 0 \\ y = \frac{1}{3} or - \frac{2}{3} \\ Substitute y into (3) : \\ When y = \frac{1}{3} \\ x = 3 (\frac{1}{3}) + 1 = 2 \\ When y = - \frac{2}{3} \\ x = 3 (- \frac{2}{3}) + 1 = - 1 \\ Hence, the solutions are x = 2, y = \frac{1}{3} or x = - 1, y = - \frac{2}{3} . \end{array}

Long Question (Question 9)

Posted on May 17, 2020 by Myhometuition

Question 9 (7 marks):
Diagram shows the plan of a rectangular garden ABCD. The garden consists of a semicircular pond ATD and grassy area ABCDT.

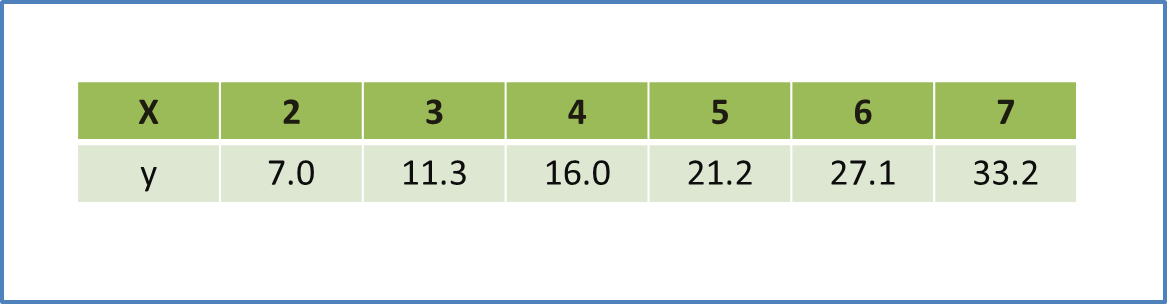
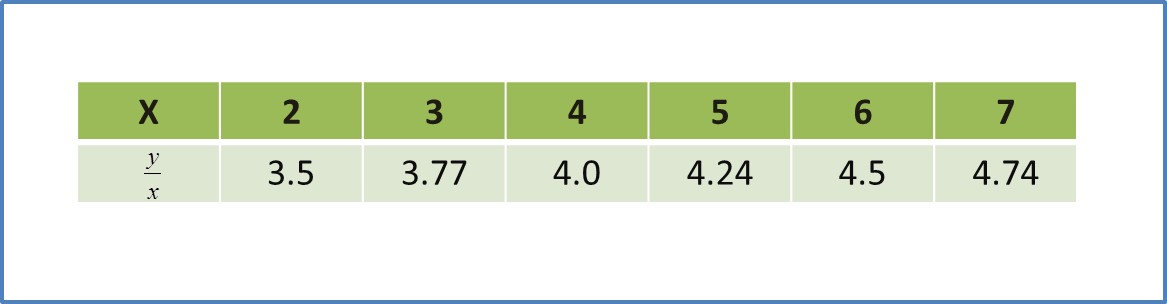
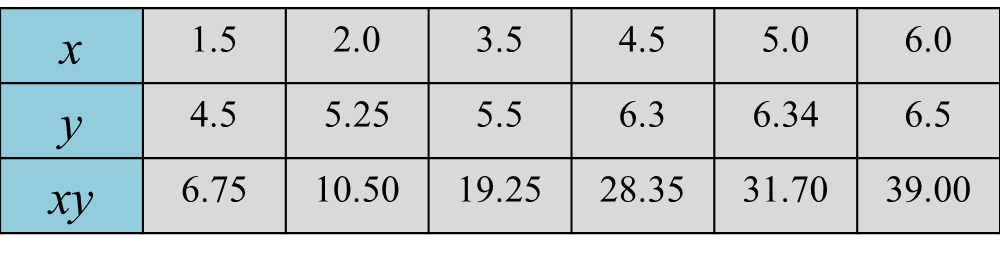
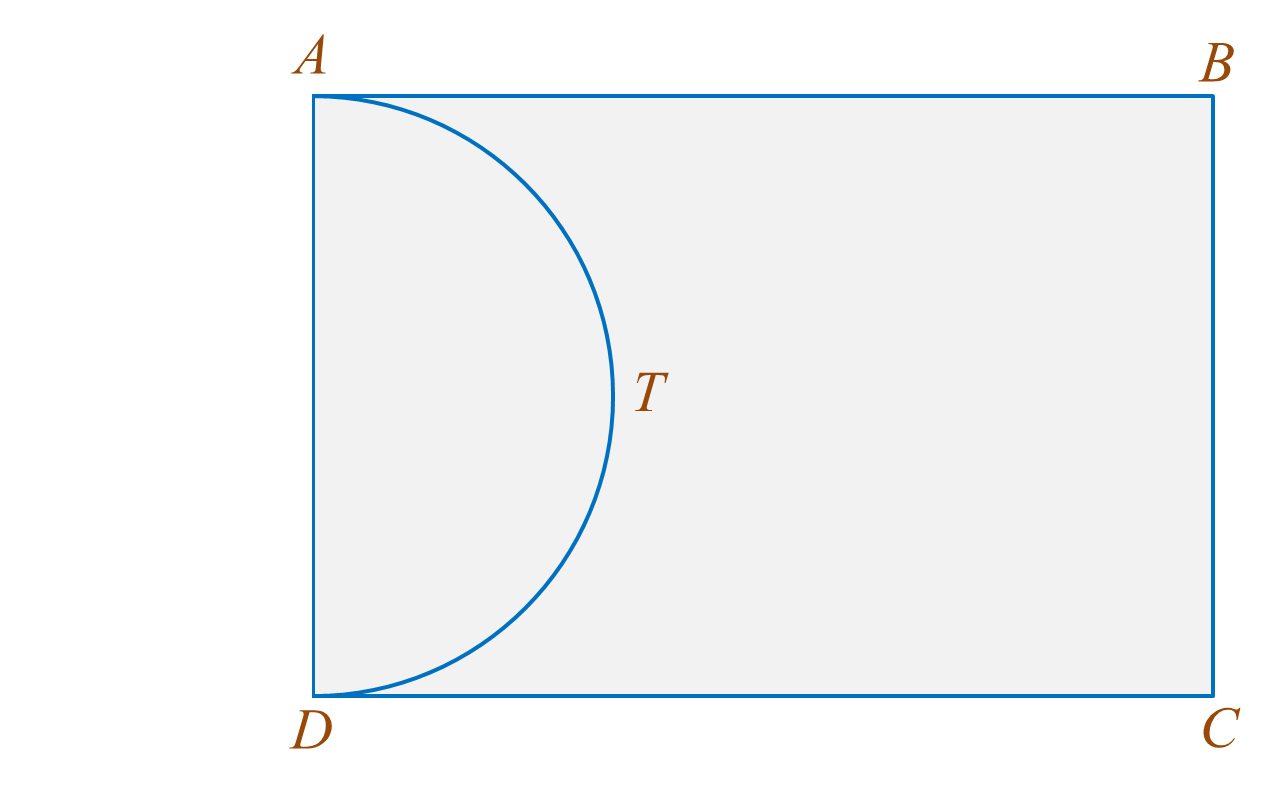It is given that DC = 6y metre and BC = 7x metre, x ≠ y. The area of the rectangular garden ABCD is 168 metre² and the perimeter of the grassy area is 60 metre. The pond with uniform depth contains 15.4 metre³ of water.
By using

π = \frac{22}{7}

, find the depth, in metre, of water in the pond.

Solution:

\begin{array}{l} Area of A B C D = 168 \\ (6 y) (7 x) = 168 \\ 42 x y = 168 \\ x y = 4................... (1) \\ Perimeter of grassy area = 60 \\ 6 y + 6 y + 7 x + (\frac{1}{2} \times 2 \times \frac{22^{11}}{7} \times \frac{7 x}{2}) = 60 \\ 12 y + 18 x = 60 \\ 2 y + 3 x = 10................... (2) \\ From (1) : x y = 4 \\ x = \frac{4}{y} ................... (3) \\ Substitute (3) into (2): \\ 2 y + 3 (\frac{4}{y}) = 10 \\ 2 y^{2} + 12 = 10 y \\ y^{2} - 5 y + 6 = 0 \\ (y - 2) (y - 3) = 0 \\ y - 2 = 0 \\ y = 2 \\ or \\ y - 3 = 0 \\ y = 3 \\ Substitute the values of y into (3): \\ When y = 2 \\ x = \frac{4}{2} = 2 (ignored, x \neq y) \\ When y = 3 \\ x = \frac{4}{3} \\ Given volume of water = 15.4 \\ \frac{1}{2} (\frac{22}{7}) {(\frac{7 x}{2})}^{2} d = 15.4 \\ \frac{1}{2} (\frac{22}{7}) {[\frac{7 (\frac{4}{3})}{2}]}^{2} d = 15.4 \\ \frac{11}{7} {(\frac{14}{3})}^{2} d = 15.4 \\ \frac{308}{9} d = 15.4 \\ d = 0.45 m \\ Thus, the depth of water in the pond is 0 .45 m . \end{array}

Long Questions (Question 5)

Posted on May 17, 2020 by Myhometuition

Question 5 (7 marks):
It is given that the equation of a curve is

y = \frac{5}{x^{2}} .

(a) Find the value of

\frac{d y}{d x}

when x = 3.
(b) Hence, estimate the value of

\frac{5}{{(2.98)}^{2}} .

Solution:
(a)

\begin{array}{l} y = \frac{5}{x^{2}} = 5 x^{- 2} \\ \frac{d y}{d x} = - 10 x^{- 3} \\ = - \frac{10}{x^{3}} \\ When x = 3 \\ \frac{d y}{d x} = - \frac{10}{3^{3}} = - \frac{10}{27} \end{array}

(b)

\begin{array}{l} δ x = 2.98 - 3 = - 0.02 \\ δ y = \frac{d y}{d x} . δ x \\ = - \frac{10}{27} \times (- 0.02) \\ = 0.007407 \\ Values of \frac{5}{{(2.98)}^{2}} \\ = y + δ y \\ = \frac{5}{x^{2}} + (0.007407) \\ = \frac{5}{3^{2}} + (0.007407) \\ = 0.56296 \end{array}

Long Questions (Question 4)

Posted on May 17, 2020 by Myhometuition

Question 4 (6 marks):
Diagram shows the front view of a part of a roller coaster track in a miniature park.

The curve part of the track of the roller coaster is represented by an equation

y = \frac{1}{64} x^{3} - \frac{3}{16} x^{2}

, with point A as the region.
Find the shortest vertical distance, in m, from the track to ground level.

Solution:

\begin{array}{l} y = \frac{1}{64} x^{3} - \frac{3}{16} x^{2} ............... (1) \\ \frac{d y}{d x} = 3 (\frac{1}{64}) x^{2} - 2 (\frac{3}{16}) x^{1} \\ = \frac{3}{64} x^{2} - \frac{3}{8} x \\ At turning point, \frac{d y}{d x} = 0 \\ \frac{3}{64} x^{2} - \frac{3}{8} x = 0 \\ x (\frac{3}{64} x - \frac{3}{8}) = 0 \\ x = 0 or \\ \frac{3}{64} x - \frac{3}{8} = 0 \\ \frac{3}{64} x = \frac{3}{8} \\ x = \frac{3}{8} \times \frac{64}{3} \\ x = 8 \\ Substitute values of x into equation (1): \\ When x = 0, \\ y = \frac{1}{64} {(0)}^{3} - \frac{3}{16} {(0)}^{2} \\ y = 0 \\ When x = 8, \\ y = \frac{1}{64} {(8)}^{3} - \frac{3}{16} {(8)}^{2} \\ y = - 4 \\ Thus, turning points : (0, 0) and (8, - 4) \end{array}

\begin{array}{l} \frac{d y}{d x} = \frac{3}{64} x^{2} - \frac{3}{8} x \\ \frac{d^{2} y}{d x^{2}} = 2 (\frac{3}{64}) x - \frac{3}{8} \\ = \frac{3}{32} x - \frac{3}{8} \\ When x = 0, \\ \frac{d^{2} y}{d x^{2}} = \frac{3}{32} (0) - \frac{3}{8} \\ = - \frac{3}{8} (< 0) \\ (0, 0) is maximum point . \\ When x = 8, \\ \frac{d^{2} y}{d x^{2}} = \frac{3}{32} (8) - \frac{3}{8} \\ = \frac{3}{8} (> 0) \\ (8, - 4) is minimum point . \\ Shortest vertical distance between track \\ and ground level is at the minimum point . \\ Shortest vertical distance \\ = 5 - 4 \\ = 1 m \end{array}

Long Questions (Question 10)

Posted on May 17, 2020 by Myhometuition

Question 10 (8 marks):
Diagram shows a circle and a sector of a circle with a common centre O. The radius of the circle is r cm.

It is given that the length of arc PQ and arc RS are 2 cm and 7 cm respectively. QR = 10 cm.
[Use θ = 3.142]
Find
(a) the value of r and of θ,
(b) the area, in cm², of the shaded region.

Solution:
(a)

\begin{array}{l} Length of arc P Q = 2 cm \\ r θ = 2 ................. (1) \\ Length of arc R S = 7 cm \\ (r + 10) θ = 7 \\ r θ + 10 θ = 7 ................. (2) \\ Substitute (1) into (2) : \\ 2 + 10 θ = 7 \\ 10 θ = 5 \\ θ = \frac{5}{10} \\ θ = 0.5 rad \\ From (1) : \\ When θ = 0.5 rad, \\ r \times 0.5 = 2 \\ r = 4 \end{array}

(b)

\begin{array}{l} O S = O R = 4 + 10 = 14 cm \\ Area of shaded region \\ = area of Δ O R S - area of sector O P Q \\ = (\frac{1}{2} \times 14^{2} \times \sin 0.5 rad) - (\frac{1}{2} \times 4^{2} \times 0.5) \\ = 42.981 {cm}^{2} \end{array}