Quadratic Functions, SPM Practice (Long Questions)

Question 5:


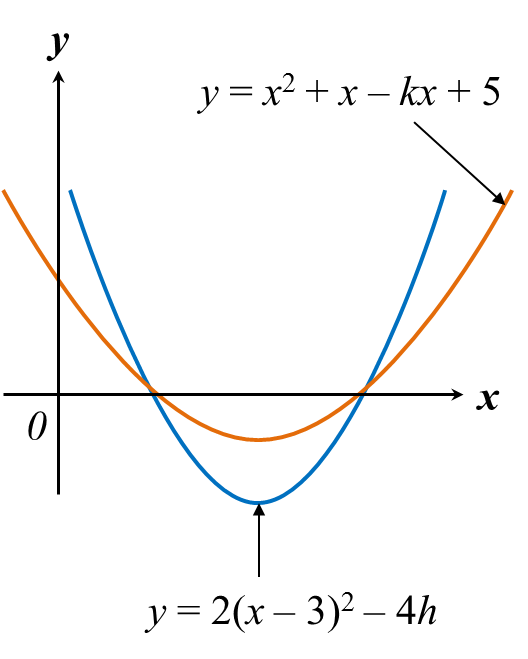
Diagram above shows the graphs of the curves y = x² + x – kx + 5 and y = 2(x – 3) – 4h that intersect the x-axis at two points. Find
(a) the value of k and of h,
(b) the minimum value of each curve.


Solution:
(a)
$\begin{array}{l}y=x^2+x-kx+5\\ =x^2+\left(1-k\right)x+5\\ ={\left[x+\frac{\left(1-k\right)}{2}\right]}^2-{\left(\frac{1-k}{2}\right)}^2+5\\ \text{axis of symmetry of the graph is}\\ x=-\frac{\left(1-k\right)}{2}\end{array}$

$\begin{array}{l}y=2{\left(x-3\right)}^2-4h\\ \text{axis of symmetry of the graph is }x=3.\\ \therefore -\frac{1-k}{2}=3\\ -1+k=6\\ k=7\end{array}$

$\begin{array}{l}\text{Substitute }k=7\text{ into equation}\\ y=x^2+x-7x+5\\ =x^2-6x+5\\ \text{At }x\text{-axis},y=0;\\ x^2-6x+5=0\\ \left(x-1\right)\left(x-5\right)=0\\ x=1,5\end{array}$

$\begin{array}{l}\text{At point }\left(1,0\right)\\ \text{Substitute }x=1,y=0\text{ into the graph:}\\ y=2{\left(x-3\right)}^2-4h\\ 0=2{\left(1-3\right)}^2-4h\\ 4h=2\left(4\right)\\ 4h=8\\ h=2\end{array}$

(b)
$\begin{array}{l}\text{For }y=x^2-6x+5\\ ={\left(x-3\right)}^2-9+5\\ ={\left(x-3\right)}^2-4\\ \therefore \text{ Minimum value is }-4.\\ \\ \text{For }y=2{\left(x-3\right)}^2-8,\text{ minimum value is}-8.\end{array}$