Long Questions (Question 4)

Question 4:

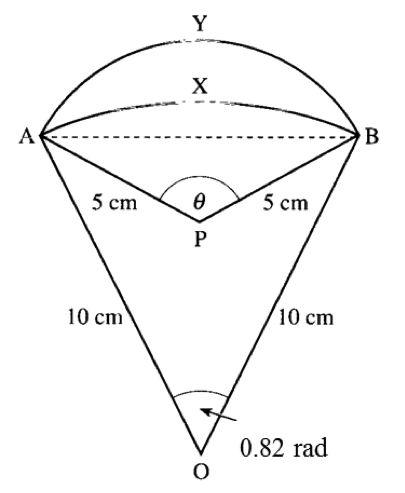
In the diagram above, AXB is an arc of a circle centre O and radius 10 cm with ∠AOB = 0.82 radian. AYB is an arc of a circle centre P and radius 5 cm with ∠APB = θ. Calculate:

1. the length of the chord AB,
   
2. the value of θ in radians,
3. the difference in length between the arcs AYB and AXB.

Solution:

(a)
 $\begin{array}{l}\frac{1}{2}AB=\sin 0.41\times 10\to \left(\text{Change the calculator to Rad mode}\right)\\ \frac{1}{2}AB=3.99\\ \therefore \text{The length of chord}AB=3.99\times 2=7.98cm.\end{array}$

(b)
 $\begin{array}{l}\text{Let}\frac{1}{2}\theta =\alpha ,\theta =2\alpha \\ \sin \alpha =\frac{3.99}{5}\\ \alpha =0.924\text{rad}\\ \therefore \theta =0.924\times 2=1.848\text{radian}\text{.}\end{array}$

(c)
Using s = rθ
Arcs AXB = 10 × 0.82 = 8.2 cm
Arcs AYB = 5 × 1.848 = 9.24 cm

Difference in length between the arcs AYB and AXB
= 9.24 – 8.2
= 1.04 cm