Short Questions (Question 3 & 4)

Posted on April 21, 2020 by user

Question 3:

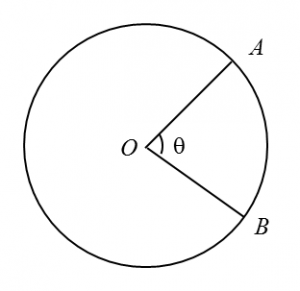
Diagram below shows a circle with centre O.

The length of the minor arc is 16 cm and the angle of the major sector AOB is 290^o.

Using π = 3.142, find

(a) the value of θ, in radians. (Give your answer correct to four significant figures)

(b) the length, in cm, of the radius of the circle.

Solution:

(a)

Angle of the minor sector AOB

= 360^o– 290^o

= 70^o

= 70^o×

\frac{3.142}{180}

= 1.222 radians

(b)

Using s = rθ

r × 1.222 = 16

radius, r = 13.09 cm

Question 4:

Diagram below shows sector OPQ with centre O and sector PXY with centre P.
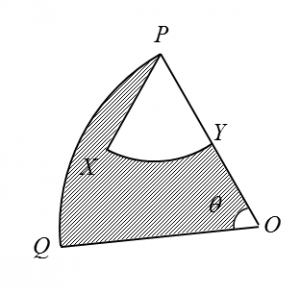Given that OQ = 8 cm, PY = 3 cm , ∠ XPY = 1.2 radians and the length of arc PQ = 6cm ,

calculate

( a) the value of θ , in radian ,

( b) the area, in cm² , of the shaded region .

Solution:
(a) s = r θ

6 = 8 θ

θ = 0.75 rad

(b)

Area of the shaded region

= Area of sector OPQ – Area of sector PXY

= \frac{1}{2} {(8)}^{2} (0.75) - \frac{1}{2} {(3)}^{2} (1.2)

= 24 – 5.4

= 18.6 cm²