5.1 Positive and Negative Angles
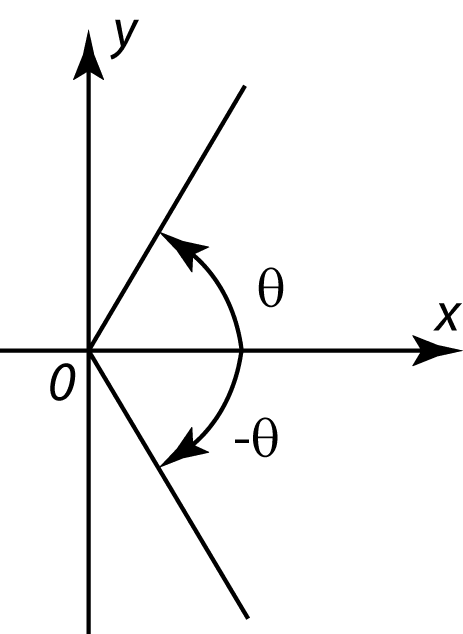
1. Positive angles are angles measure in an anticlockwise rotate from the positive x-axis about the origin, O.
2. Negative angles are angles measured in a clockwise rotation from the positive x-axis about the origin O.
3. One complete revolution is 360° or 2π radians.
Example:
Show each of the following angles on a separate diagram and state the quadrant in which the angle is situated.
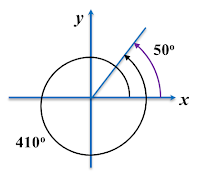
(a) 410°
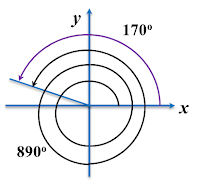
(b) 890°
(c)229π radians
(d)103π radians
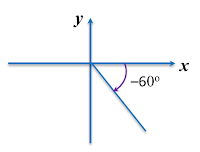
(e) –60o
(f) –500°
(g)−314π radians
Solution:
(a)
Based on the above circular diagram, the positive angle of 410° is in the first quadrant.
(b)
Based on the above circular diagram, the positive angle of 890° is in the second quadrant.
(c)
229πrad=(2π+49π)rad=360o+80o
Based on the above circular diagram, the positive angle of
229π radians
is in the first quadrant.
(d)
103πrad=(3π+13π)rad=540o+60o
Based on the above circular diagram, the positive angle of
103π radians
is in the third quadrant.
(e)
Based on the above circular diagram, the negative angle of –60° is in the fourth quadrant.
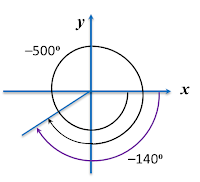
(f)
–500° = –360° – 140°
Based on the above circular diagram, the negative angle of –500° is in the third quadrant.
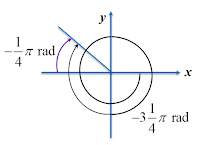
(g)
−314πrad=(−3π−14π)rad=−540o−45o
Based on the above circular diagram, the negative angle of
−314π radians
is in the second quadrant.