Question 1:
Solution:
(a)(b)
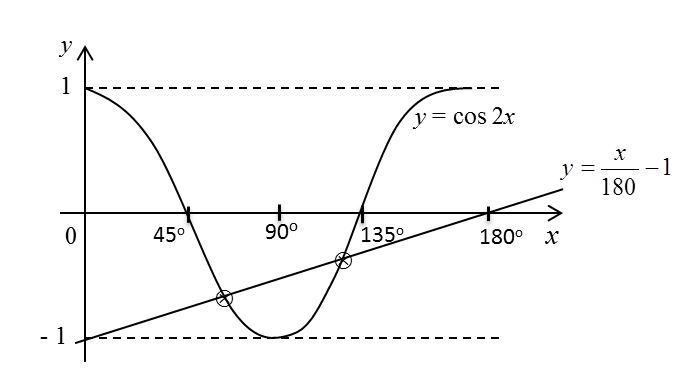
2 sin2x=2−x1801−2 sin2x=1−(2−x180)cos2x=x180−1y=x180−1x=0, y=−1x=180, y=0Number of solutions = 2
(a) Sketch the graph of y = cos 2x for 0° ≤ x ≤ 180°.
(b) Hence, by drawing a suitable straight line on the same axes, find the number of solutions satisfying the equation
2 sin2x=2−x180
for 0° ≤ x ≤ 180°.
Solution:
(a)(b)

2 sin2x=2−x1801−2 sin2x=1−(2−x180)cos2x=x180−1y=x180−1x=0, y=−1x=180, y=0Number of solutions = 2
Question 2:
(a) Sketch the graph of y=32cos2x for 0≤x≤32π.
(b) Hence, using the same axes, sketch a suitable straight line to find the number of solutions to the equation 43πx−cos2x=32 for 0≤x≤32π
State the number of solutions.
Solution:
(a)(b)
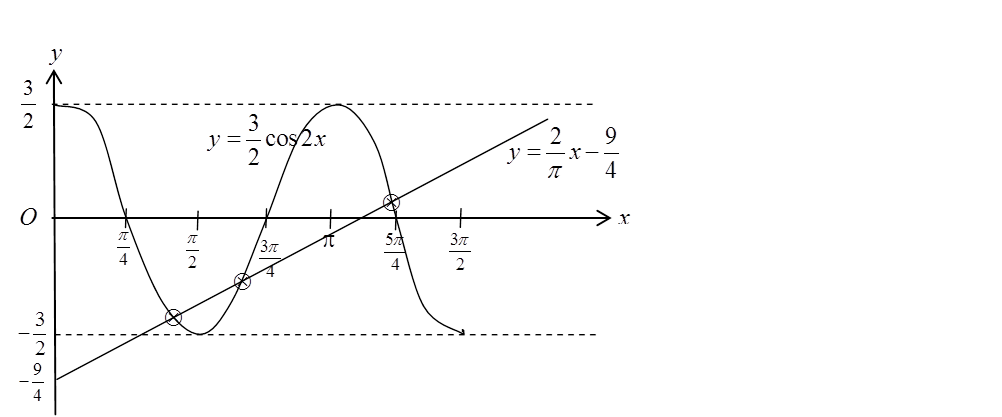
43πx−cos2x=32cos2x=43πx−3232cos2x=32(43πx−32)y=2πx−94To sketch the graph of y=2πx−94x=0, y=−94x=3π2, y=34Number of solutions =Number of intersection points= 3
(a) Sketch the graph of y=32cos2x for 0≤x≤32π.
(b) Hence, using the same axes, sketch a suitable straight line to find the number of solutions to the equation 43πx−cos2x=32 for 0≤x≤32π
State the number of solutions.
Solution:
(a)(b)
