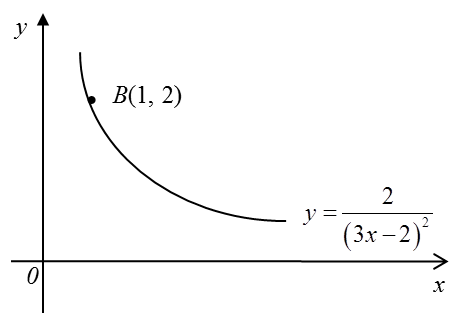Question 6:
Diagram below shows part of the curve y=2(3x−2)2 which passes through B (1, 2).
(a) Find the equation of the tangent to the curve at the point B.
(b) A region is bounded by the curve, the x-axis and the straight lines x = 2 and x = 3.
(i) Find the area of the region.
(ii) The region is revolved through 360° about the x–axis. Find the volume generated, in terms of p.
Solution:
(a)
y=2(3x−2)2=2(3x−2)−2dydx=−4(3x−2)−3(3)dydx=−12(3x−2)3dydx=−12(3(1)−2)3,x=1dydx=−12y−2=−12(x−1)y−2=−12x+12y=−12x+14
(b)(i)
Area =∫32ydx=∫322(3x−2)2dx=∫322(3x−2)−2dx=[2(3x−2)−1−1(3)]32=[−23(3x−2)]32=[−23[3(3)−2]]−[−23[3(2)−2]]=−221+16=114unit2
(b)(ii)
Volume generated=π∫y2dx=π∫324(3x−2)4dx=π∫324(3x−2)−4dx=π[4(3x−2)−3−3(3)]32=π[−49(3x−2)3]32=π[−49[3(3)−2]3]−[−49[3(2)−2]3]=π(−43087+4576)=315488πunit3
Diagram below shows part of the curve y=2(3x−2)2 which passes through B (1, 2).
(a) Find the equation of the tangent to the curve at the point B.
(b) A region is bounded by the curve, the x-axis and the straight lines x = 2 and x = 3.
(i) Find the area of the region.
(ii) The region is revolved through 360° about the x–axis. Find the volume generated, in terms of p.
(a)
y=2(3x−2)2=2(3x−2)−2dydx=−4(3x−2)−3(3)dydx=−12(3x−2)3dydx=−12(3(1)−2)3,x=1dydx=−12y−2=−12(x−1)y−2=−12x+12y=−12x+14
(b)(i)
Area =∫32ydx=∫322(3x−2)2dx=∫322(3x−2)−2dx=[2(3x−2)−1−1(3)]32=[−23(3x−2)]32=[−23[3(3)−2]]−[−23[3(2)−2]]=−221+16=114unit2
(b)(ii)
Volume generated=π∫y2dx=π∫324(3x−2)4dx=π∫324(3x−2)−4dx=π[4(3x−2)−3−3(3)]32=π[−49(3x−2)3]32=π[−49[3(3)−2]3]−[−49[3(2)−2]3]=π(−43087+4576)=315488πunit3