Question 7:
Solution:
 (a)
(a)
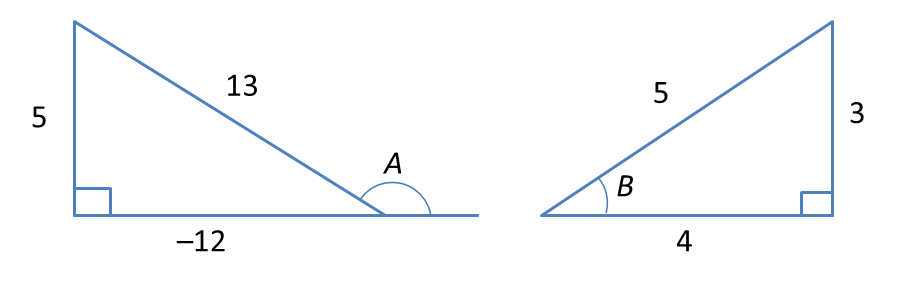
tanA=−512
(b)
sin(A+B)=sinAcosB+cosAsinBsin(A+B)=(513)(45)+(−1213)(35)←cosA=−1213sinB=35sin(A+B)=413−3665sin(A+B)=−1665
(c)
cos(A−B)=cosAcosB+sinAsinBcos(A−B)=(−1213)(45)+(513)(35)cos(A−B)=−3365
It is given that
sinA=513andcosB=45
, where A is an obtuse angle and B is an acute angle.
Find
(a) tan A
(b) sin (A + B)
(c) cos (A – B)
 (a)
(a)tanA=−512
(b)
sin(A+B)=sinAcosB+cosAsinBsin(A+B)=(513)(45)+(−1213)(35)←cosA=−1213sinB=35sin(A+B)=413−3665sin(A+B)=−1665
(c)
cos(A−B)=cosAcosB+sinAsinBcos(A−B)=(−1213)(45)+(513)(35)cos(A−B)=−3365
Question 8:
Solution:
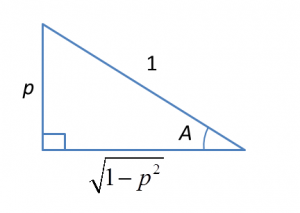 Using Pythagoras Theorem,Adjacent side=√12−p2=√1−p2
Using Pythagoras Theorem,Adjacent side=√12−p2=√1−p2
(a)
tanA=−p√1−p2←tan is negative atsecond quadrant
(b)
cosA=−√1−p2←cosis negative atsecond quadrant
(c)
sinA=2sinAcosAsinA=2(p)(−√1−p2)sinA=−2p√1−p2
If sin A = p, and 90° < A < 180°, express in terms of p
(a) tan A
(b) cos A
(c) sin 2A
Solution:
 Using Pythagoras Theorem,Adjacent side=√12−p2=√1−p2
Using Pythagoras Theorem,Adjacent side=√12−p2=√1−p2
(a)
tanA=−p√1−p2←tan is negative atsecond quadrant
(b)
cosA=−√1−p2←cosis negative atsecond quadrant
(c)
sinA=2sinAcosAsinA=2(p)(−√1−p2)sinA=−2p√1−p2