6.3 Combinations
(1) The number of combinations of r objects chosen from n different objects is given by :
nCr=n!r!(n−r)!
(2) A combination of r objects chosen from n different objects is a selection of a set of r objects chosen from n objects. The order of the objects in the chosen set is not taken into consideration.
Note:(i)nC0=1(ii)nCn=1(iii)nCr=nCn−r
Note:(i)nC0=1(ii)nCn=1(iii)nCr=nCn−r
Example 1:
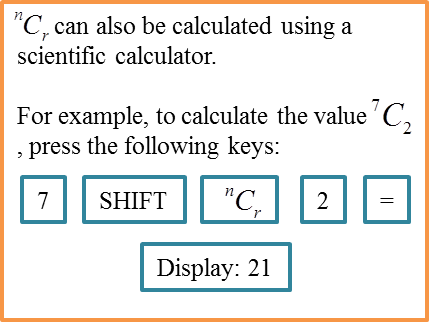
Calculate the value of 7C27C2=7!(7−2)! ×2!=7!5! ×2!=7 ×6 ×5!5! ×2!=7×62×1=21
Calculator Computation:
Calculate the value of 7C27C2=7!(7−2)! ×2!=7!5! ×2!=7 ×6 ×5!5! ×2!=7×62×1=21
Calculator Computation:
Example 2:
There are 6 marbles, each with different colour, which are to be divided equally between 2 children. Find the number of different ways the division of the marbles can be done.
Solution:
Number of ways giving 3 marbles to the first child =
6C3
Number of ways giving the remaining 3 marbles =
3C3
So, the number of different ways the division of the marbles
=6C3×3C3=20×1=20
=6C3×3C3=20×1=20