9.4.3 Shortest Distance between Two Points
1. The shortest distance between two points on the surface of the earth is the distance measured along a great circle.
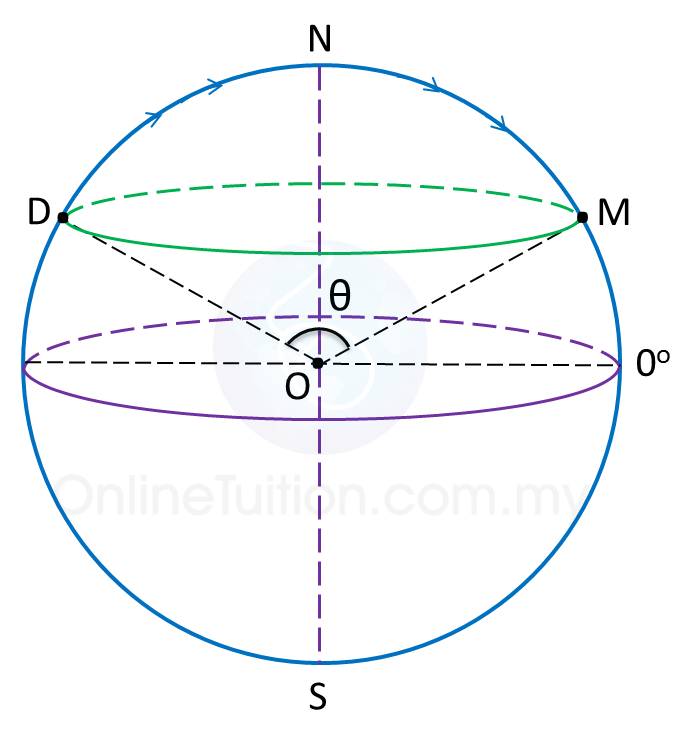

|
Shortest distance between points D and M
= ( θ × 60 ) nautical miles
|
Example:
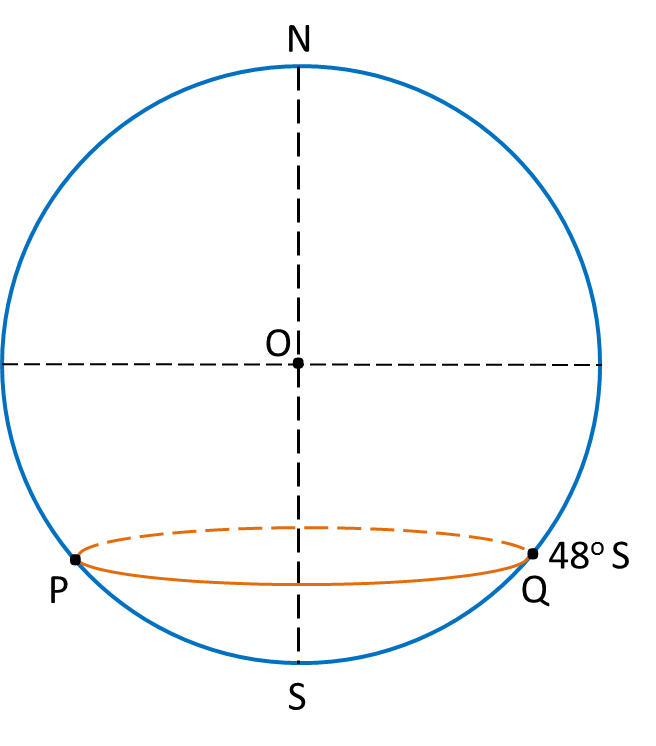

In the above diagram, calculate
(a) The distance from P to Q, measured along the parallel of latitude 48o S,
(b) The distance from P to Q, measured along the route PSQ, where S is the South Pole.
State the shorter distance.
Solution:
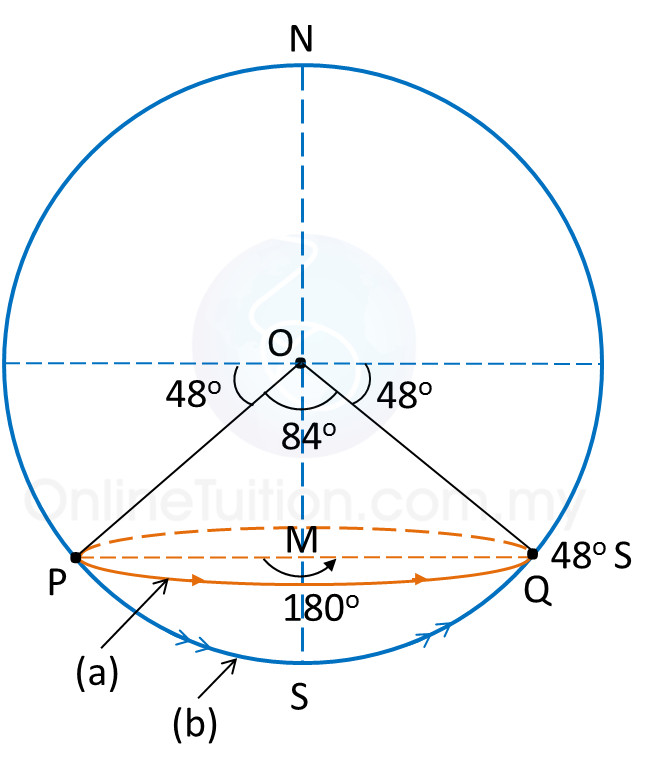
(a)
Distance from Pto Q, measured along the parallel of latitude 48o S
= 180 × 60 × cos 48o← (angle PMQ = 180o)
= 7266.61 n.m.
(b)
Distance from Pto Q, measured along the route PSQ, where S is the South Pole
= 84 × 60 ← (angle POQ = 180o – 48o – 48o = 84o)
= 5040 n.m.
The distance from P to Q, measured along the route PSQ in (b), where S is the South Pole, is shorter than the distance measured along the parallel of latitude in (a).
|
The shortest distance in the above example is
the distance along the arc of a great circle,
which passes through the South (or North) Pole.
|