9.6 SPM Practice (Long Questions)

Question 7 (12 marks):
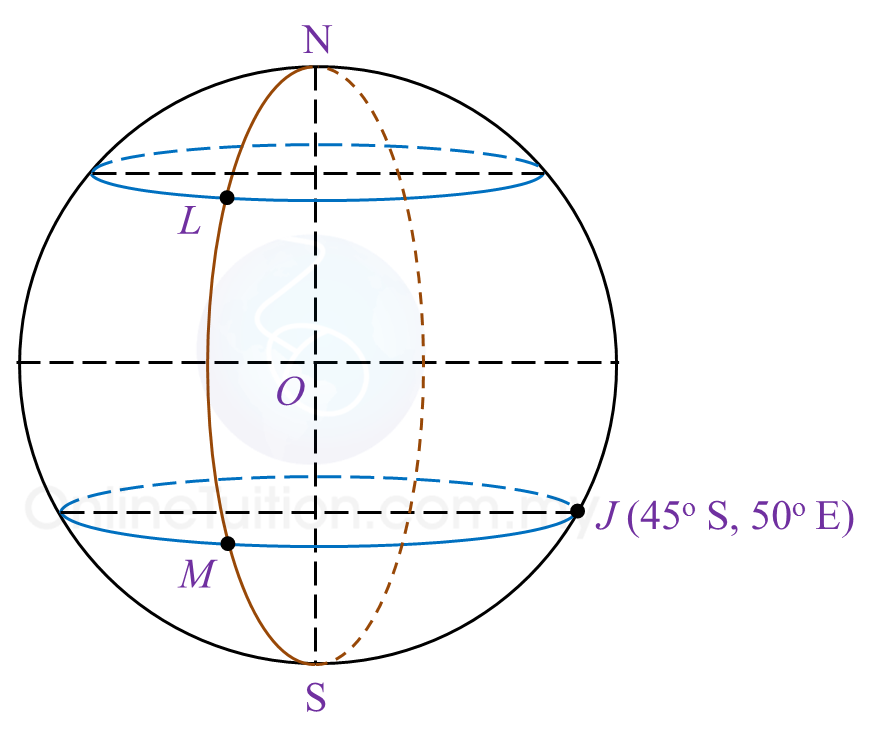
Diagram 7 in the answer space shows the locations of points J, L and M, which lie on the surface of the earth. O is the centre of the earth. The longitude of M is 30^o W. K is another point on the surface of the earth such that KJ is the diameter of the common parallel of latitude 45^o S.

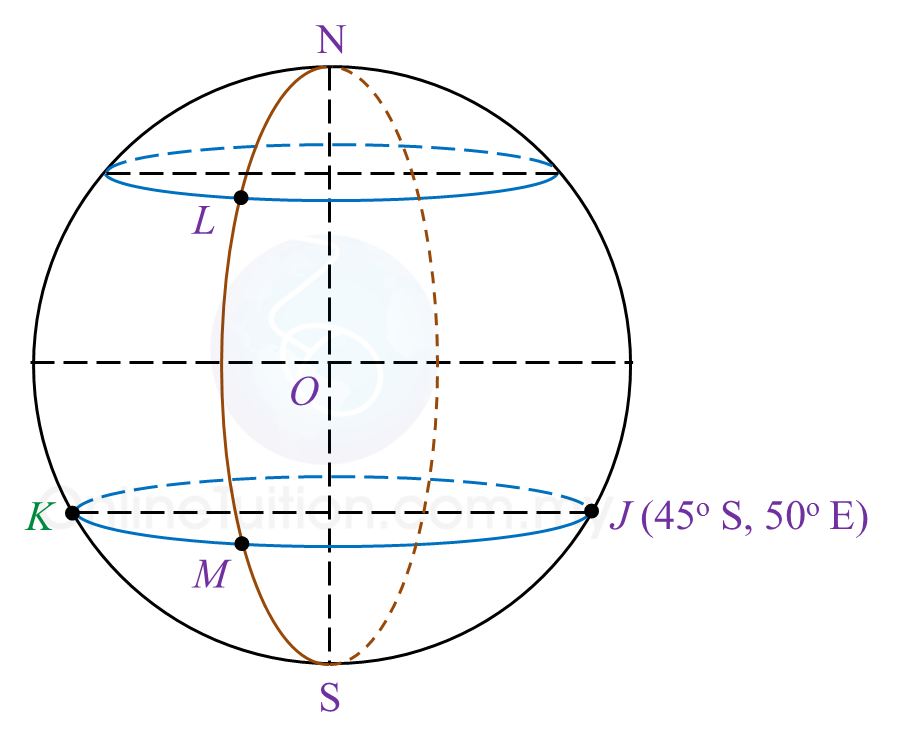
(a)(i) Mark and label point K on Diagram 7 in the answer space.

(ii) Hence, state the longitude of point K.

(b) L lies due north of M and the shortest distance from M to L measured along the surface of the earth is 7500 nautical miles.
Calculate the latitude of L.

(c) Calculate the distance, in nautical mile, from K due east to M measured along the common parallel of latitude.

(d) An aeroplane took off from K and flew due east to M along the common parallel of latitude. The average speed of the aeroplane for the flight was 750 knots.
Calculate the total time, in hour, taken for the whole flight.



Answer:



Solution:
(a)(i)


(a)(ii)
Longitude of point K = 130^oW

(b)
$\begin{array}{l}\angle LOM\times 60=7500\\ \angle LOM=\frac{7500}{60}\\ \angle LOM={125}^o\\ \\ \text{Latitude of }L={125}^o-{45}^o\\ ={80}^{o}N\end{array}$

(c)
KM = (130^o – 30^o) × 60 × cos 45^o
= 4242.64 nautical miles

(d)
$\begin{array}{l}\text{Time}=\frac{\text{Distance}}{\text{speed}}\\ =\frac{4242.64}{750}\\ =5.66\text{ hours}\end{array}$