9.3 SPM Practice (Short Questions)

Posted on April 23, 2020 by user

Question 13:

Which of the following graph represents y = tan x for 0^o ≤ x ≤ 360^o?

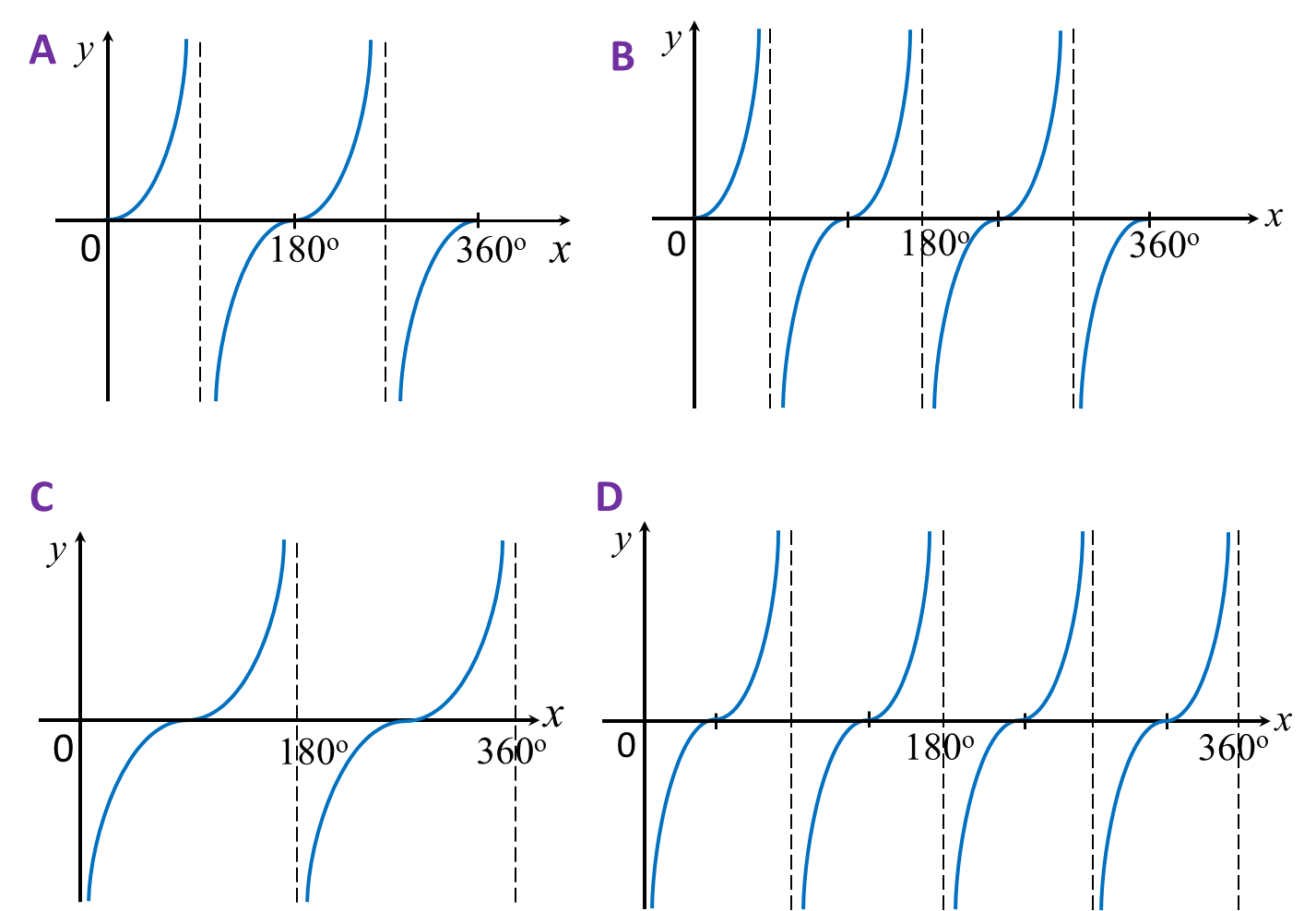
Solution:

Answer: A

Question 14:

Which graph represents part of y = tan x?

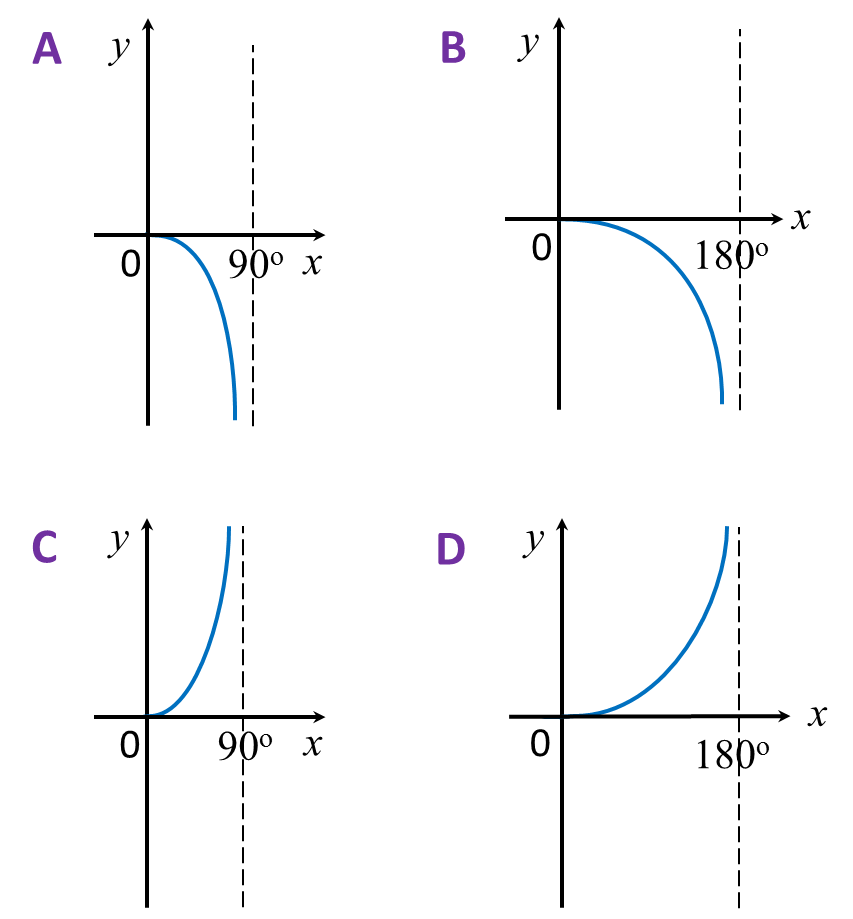
Solution:

Answer: C

9.2 Graphs of Sine, Cosine and Tangent

Posted on April 23, 2020 by user

9.2 Graphs of Sine, Cosine and Tangent

(1) y = sin x, 0^o≤ x ≤ 360^o

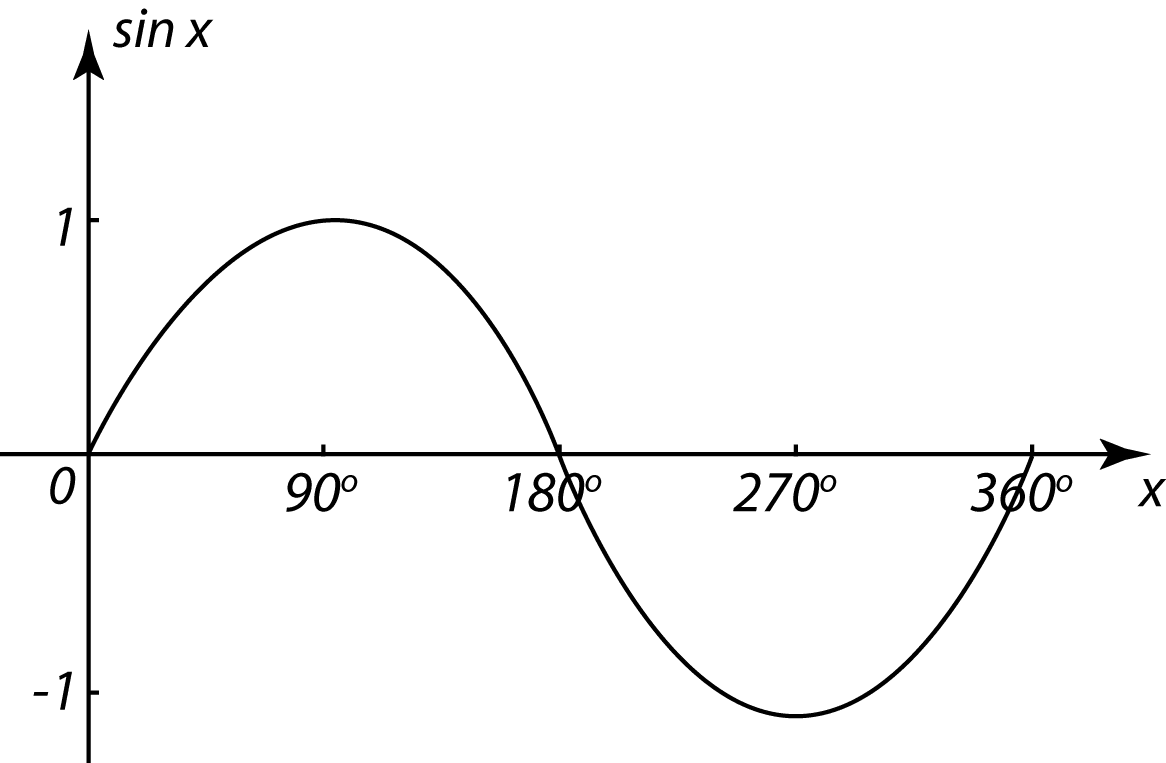
x	0^o	90^o	180^o	270^o	360^o
*sin x*	0	1	0	-1	0

(2) y = cos x, 0^o≤ x ≤ 360^o

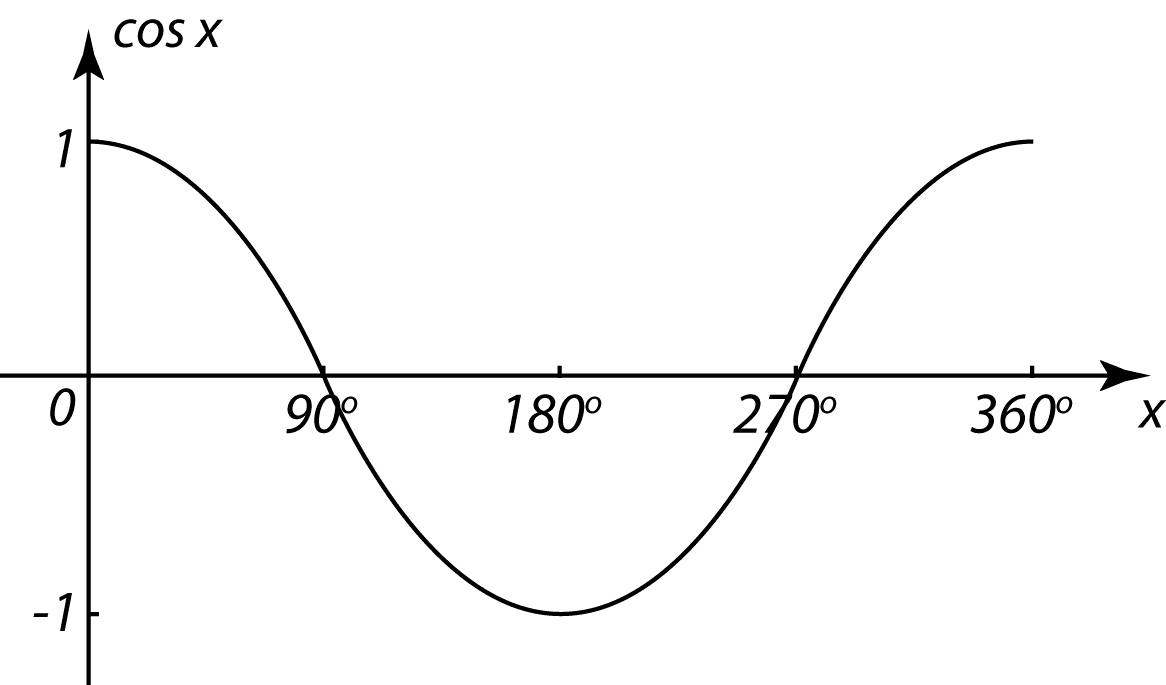
x	0^o	90^o	180^o	270^o	360^o
*cos x*	1	0	-1	0	1

(3) y = tan x, 0^o≤ x ≤ 360^o

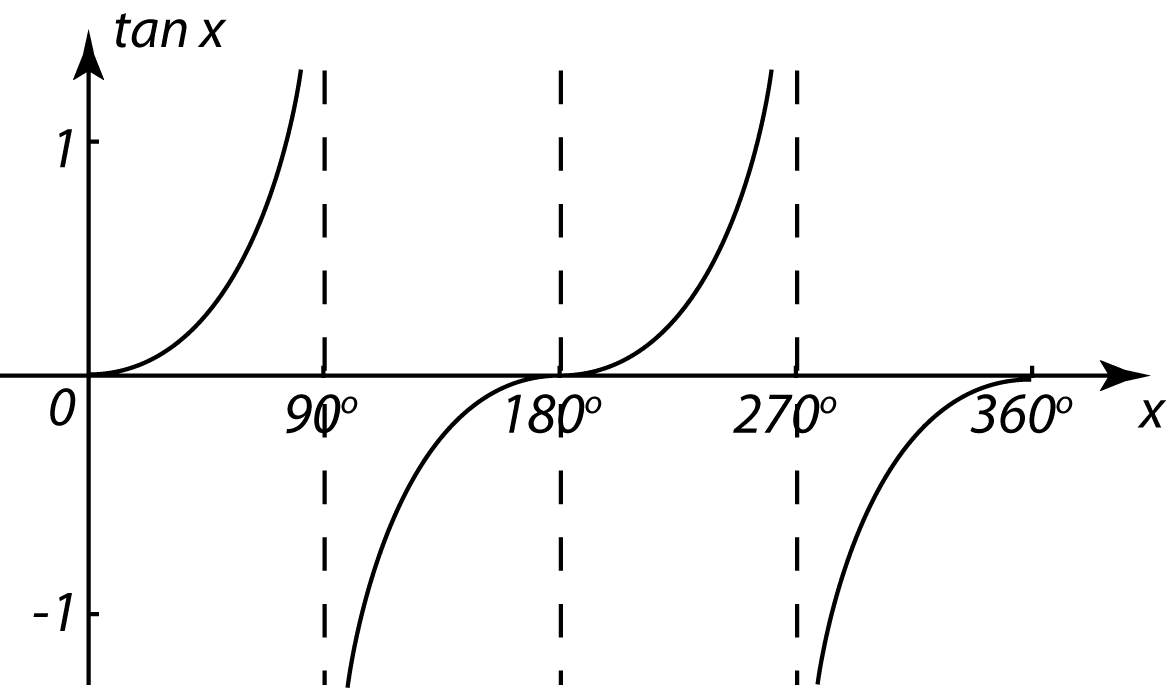
x	0^o	90^o	180^o	270^o	360^o
*tan* x	0	∞	0	∞	0

(4) y = sin 2x, 0^o≤ 2x ≤ 360^o
(5) y = cos 2x, 0^o≤ 2x ≤ 360^o

(6) y = tan 2x, 0^o≤ 2x ≤ 360^o

9.1 Values of Sine, Cosine and Tangent of an Angle (Part 1)

Posted on April 23, 2020 by user

9.1 Values of Sine, Cosine and Tangent of an Angle

(A) Sine, Cosine and Tangent for Right-Angled Triangles

\begin{array}{l} \sin θ = \frac{opposites side}{hypotenuse} \\ cos θ = \frac{adjacent side}{hypotenuse} \\ tan θ = \frac{opposites side}{adjacent side} \end{array}

(B) Values of Sin θ, Cos θ and Tan θ in First Quadrant of the Unit Circle

In first quadrant, P is a point on the circumference of the unit circle with centre O, θ is the angle between the radius OP and the positive x-axis. From the diagram,

\begin{array}{l} (a) sin θ = \frac{P Q}{O P} = y \\ (b) cos θ = \frac{O Q}{O P} = x \\ (c) tan θ = \frac{P Q}{O Q} = \frac{y}{x} \\ T h e r e f o r e, \\ \begin{array}{l} sin θ = y -coordinate \\ cos θ = x -coordinate \\ tan θ = \frac{y -coordinate}{x -coordinate} \end{array} \end{array}

(C) A Cartesian plane is divided into four parts called quadrants by the x-axis and the y-axis. The quadrants are named as first quadrant, second quadrant, third quadrant and fourth quadrant in the anticlockwise direction.

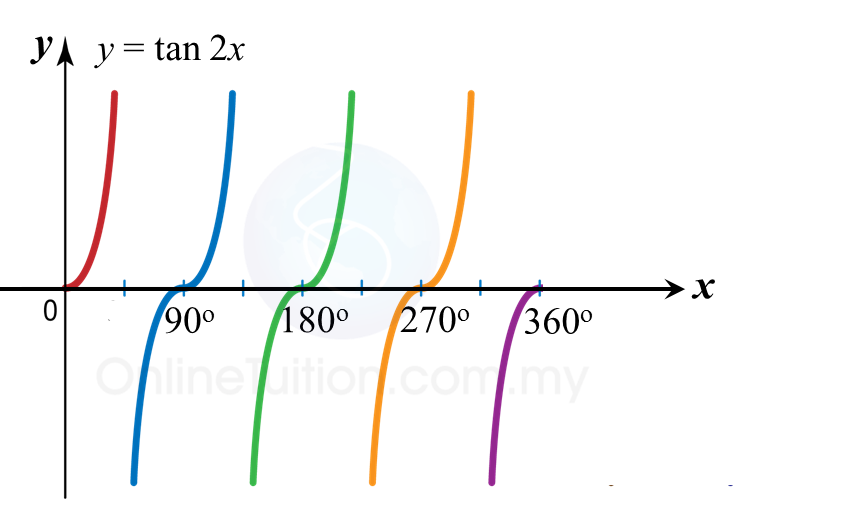
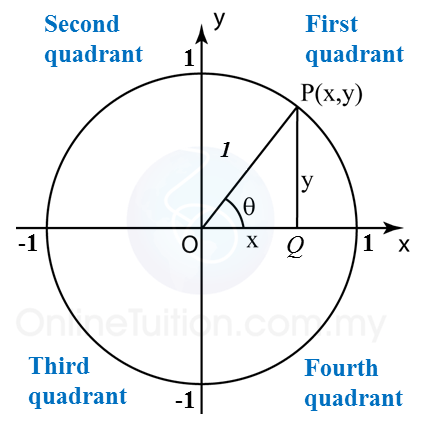
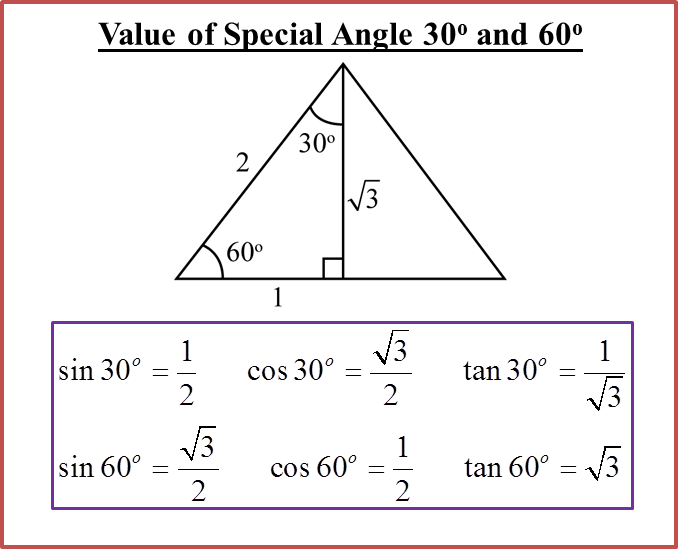
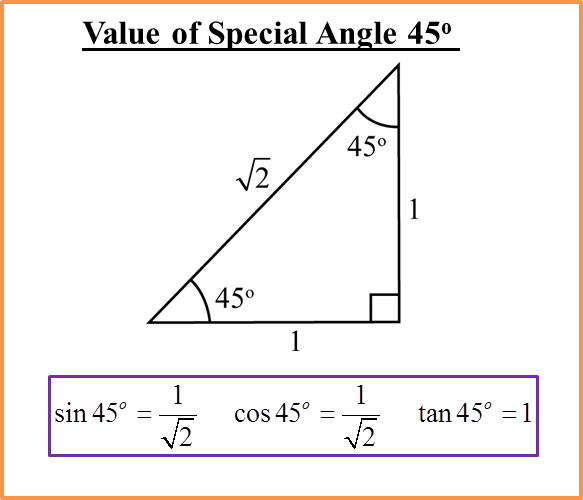
Quick recall:

All – Add

Sine – Sugar

Tangent – To

Cosine – Coffee

Example:

Determine whether the value of each of the following is positive or negative.

(a) sin 105^o (b) cos 75^o (c) tan 305^o (d) sin 50^o

(e) cos 160^o (f) tan 220^o (g) cos 260^o (h) cos 350^o

Solution:

(a) sin 105^o is positive because 90^o< 105^o< 180^o (in second quadrant).

(b) cos 75^o is positive because 0^o< 75^o< 90^o (in first quadrant).

(c) tan 305^o is negative because 270^o< 305^o< 360^o (in fourth quadrant).

(d) sin 50^o is positive because 0^o< 50^o< 90^o (in first quadrant).

(e) cos 160^o is negative because 90^o< 160^o< 180^o (in second quadrant).

(f) tan 220^o is positive because 180^o< 220^o< 270^o (in third quadrant).

(g) cos 260^o is negative because 180^o< 260^o< 270^o (in third quadrant).

(h) cos 350^o is positive because 270^o< 350^o< 360^o (in fourth quadrant).

9.3 SPM Practice (Short Questions)

Posted on April 23, 2020 by user

Question 4:

In the diagram above, WZY is a straight line.

∠ X Y Z = 90^{o}, ∠ X W Z = 30^{o}

and WZ = XZ = 30 cm. Find the length of XY.

Solution:

\begin{array}{l} ∠ W X Z = ∠ X W Z = 30^{o} \\ ∴ ∠ X Z Y = 30^{o} + 30^{o} = 60^{o} \\ \sin ∠ X Z Y = \frac{X Y}{X Z} \\ \sin 60^{o} = \frac{X Y}{30} \\ X Y = \sin 60^{o} \times 30 \\ X Y = 25.98 c m \end{array}

Question 5:

In the diagram above, PQS is a right angle triangle. Given that SR = 6cm, PQ = 12 cm and 5SR = 2PS. Find the value of cos α and tan β.

Solution:

\begin{array}{l} 5 S R = 2 P S \\ P S = \frac{5}{2} S R \\ P S = \frac{5}{2} (6) \\ P S = 15 c m \\ \cos α = \frac{P Q}{P S} \\ \cos α = \frac{12}{15} = \frac{4}{5} \\ In △ P Q S, using Pythagoras' Theorem, \\ Q S = \sqrt{P S^{2} - P Q^{2}} \\ Q S = \sqrt{15^{2} - 12^{2}} = 9 c m \\ \tan β = - \tan ∠ P S Q \leftarrow \begin{array}{l} Since 90^{\circ} < β < 180^{\circ} \\ (in quadrant II), tan β is negative \end{array} \\ \tan β = - \frac{P Q}{Q S} \\ \tan β = - \frac{12}{9} = - \frac{4}{3} \end{array}

Question 6:

In the diagram above, ADC is a straight line, if

\sin q = \frac{3}{5} and \tan p = \frac{1}{2}

. Find the distance of AC.

Solution:

\begin{array}{l} Given \sin q = \frac{B D}{A B} = \frac{3}{5} \\ \frac{B D}{30} = \frac{3}{5} \\ B D = \frac{3}{5} \times 30 \\ B D = 18 c m \\ In △ A B D, using Pythagoras' Theorem, \\ A D = \sqrt{A B^{2} - B D^{2}} \\ A D = \sqrt{30^{2} - 18^{2}} = 24 c m \\ Given tan p = \frac{B D}{D C} = \frac{1}{2} \\ \frac{18}{D C} = \frac{1}{2} \\ D C = 36 c m \\ Hence, distance of A C = 24 + 36 = 60 c m . \end{array}

9.1 Values of Sine, Cosine and Tangent of an Angle (Part 2)

Posted on April 23, 2020 by user

(A) Special Angle

(B) Finding the Angles between 0^oand 360^o Given Values of sin θ, cos θ or tan θ

1. If the value of sin θ, cos θ or tan θ is given and 0^o< θ < 360^o, the value of θ can be found using the following steps.

(a) Find the basic angle in first quadrant which corresponds to θ.

(b) Based on the sign of the value of sin θ, cos θ or tan θ, determine the quadrants in which θ lies.

(c) Find the values of θ in the right quadrants found in (b).

Example:

For each of the following cases, find the value of θ.

(a) sin θ = 0.6025 and 90^o< θ < 180^o

(b) cos θ = –0.6025 and 180^o< θ < 270^o

(c) sin θ = –0.8387 and 0^o< θ < 360^o

(d) tan θ = –1.732 and 0^o< θ < 360^o

Solution:

(a)

sin θ = 0.6025

Basic ∠ = 37.05^o ← (Press SHIFT sin^-1 0.6025 =Display: 37.04976)
∴ θ = 180^o – 37.05^o= 142.95^o ← (90^o< θ < 180^o)

(b)

cos θ = –0.6025

Basis ∠ = 52.95^o ← (Press SHIFT cos^-1 0.6025 = Display: 52.9508)

∴ θ = 180^o + 52.95^o= 232.95^o ← (180^o< θ < 270^o)

(c)

sin θ = –0.8387 ← (sin θ is negative in 3^rd quadrant and 4^thquadrant)

Basis ∠ = 57^o ← (Press SHIFT sin^-1 0.8387 = Display: 57.003)

θ₁ = 180^o + 57^o = 237^o ← (180^o< θ < 270^o)

θ₂ = 360^o – 57^o = 303^o ← (270^o< θ < 360^o)

∴ θ = 237^oand 303^o

(d)

tan θ = –1.732 ← (tan θ is negative in 2^nd quadrant and 4^thquadrant)

Basis ∠ = 60^o ← (Press SHIFT tan^-1 1.732 = Display: 59.9993)

θ₁ = 180^o – 60^o = 120^o ← (90^o< θ < 180^o)

θ₂ = 360^o – 60^o = 300^o ← (270^o< θ < 360^o)
∴ θ = 120^oand 300^o

8.3 Common Tangents (Sample Questions)

Posted on April 23, 2020 by user

Example 1:

In the diagram, ABG and CDG are two common tangents to the circle with centres O and F respectively. Find the values of

(a) x, (b) y, (c) z.

Solution:

(a)

In ∆ BFG,

angle BFG = ½ × 56^o = 28^o

angle FBG = 90^o ← (tangent is 90^o to radius)

x^o+ 28^o + 90^o = 180^o

x^o= 180^o – 118^o

x^o= 62^o

x = 62

(b)

angle AOF = x^o = 62^o← (AO// BF)

y^o= 2 × 62^o

y^o= 124^o

y = 124

(c)

Exterior angle of AOC = 360^o – 124^o = 236^o

Angle EOC = ½ × 236^o = 118^o

z^o= (180^o – 118^o) × ½ ← (∆ EOC is isosceles triangle, angle OEC = angle OCE)

z^o= 31^o

z = 31

SPM Practice (Short Questions)

Posted on April 23, 2020 by user

Question 4:

In figure above, ABCD is a tangent to the circle CEF at point C. EGC is a straight line. The value of y is

Solution:

\begin{array}{l} ∠ C E F = ∠ D C F = 70^{\circ} \\ ∠ A E G + 70^{\circ} + 210^{\circ} = 360^{\circ} \\ ∠ A E G = 80^{\circ} \\ In cyclic quadrilateral A B G E, \\ ∠ A B G + ∠ A E G = 180^{\circ} \\ y^{\circ} + 80^{\circ} = 180^{\circ} \\ y = 100 \end{array}

Question 5:

In figure above, PAQ is a tangent to the circle at point A. AEC and BED are straight lines. The value of y is

Solution:

∠ABD = ∠ACD = 40^o

∠ACB = ∠PAB = 60^o

y= 180^o– ∠ACB – ∠CBD – ∠ABD

y= 180^o– 60^o – 25^o– 40^o = 55^o

Question 6:

In figure above, KPL is a tangent to the circle PQRS at point P. The value of x is

Solution:

∠PQS = ∠SPL= 55^o

∠SPQ = 180^o– 30^o – 55^o= 95^o

In cyclic quadrilateral,

∠SPQ + ∠SRQ = 180^o

95^o+ x^o = 180^o

x = 85^o

8.3 Common Tangents (Part 1)

Posted on April 23, 2020 by user

8.3 Common Tangents

A common tangent to two circles is a straight line that touches each of the circles at only one point.

1. Intersect at two points

(a) Circles of the same size

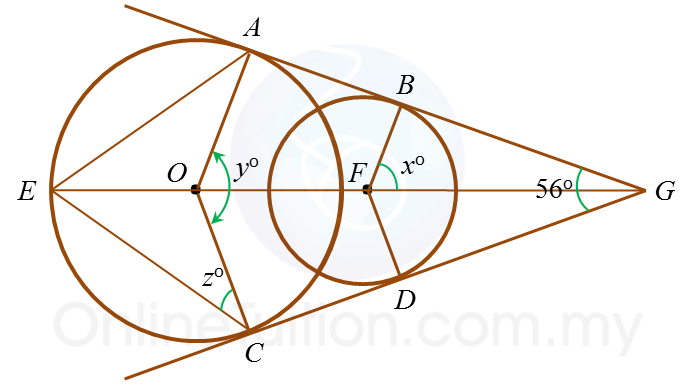
Number of common tangents	Properties of common tangents
Two common tangents: AB and CD	AC = BD AB = CD AB parallel to // OR parallel to // CD

(b) Circles of different sizes

Number of common tangents	Properties of common tangents
Two common tangents: ABE and CDE	AB = CD BE = DE OA // RB OC // RD

SPM Practice (Short Questions)

Posted on April 23, 2020 by user

Question 7:

In figure above, APB is a tangent to the circle PQR at point P. QRB is a straight line. The value of x is

Solution:

∠PQR = ∠RPB = 45^o

∠QPR = (180^o– 45^o) ÷ 2 = 67.5^o

∠PQR + ∠BPQ + x^o = 180^o

45^o+ (67.5^o + 45^o) + x^o = 180^o

x = 22.5^o

Question 8:

The figure above shows two circles with respective centres O and V. AB is a common tangent to the circles. OPRV is a straight line. The length, in cm, of PR is

Solution:

\begin{array}{l} \cos 86^{o} = \frac{O M}{O V} \\ 0.070 = \frac{1}{O V} \\ O V = \frac{1}{0.070} \\ O V = 14.29 c m \\ ∴ P R = 14.29 - 5 - 4 \\ = 5.29 c m \end{array}

8.1 Tangents to a Circle

Posted on April 23, 2020 by user

8.1 Tangents to a Circle

1. A tangent to a circle is a straight line that touches the circle at only one point and the point is called the point of contact.

2. If a straight line cuts a circle at two distinct points, it is called a secant. The chord is part of the secant in a circle.

3. Tangent to a circle is perpendicular to the radius of the circle that passes through the point of contact.

If ABC is the tangent to the circle at B, then

∠

ABO =

∠

CBO = 90^o.

Properties of Two Tangents to a Circle from an External Point

In the diagram, BA and BC are two tangents from an external point B. The properties of the tangents are as follows.

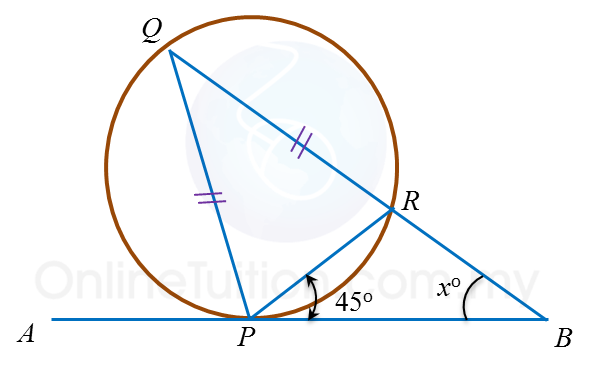
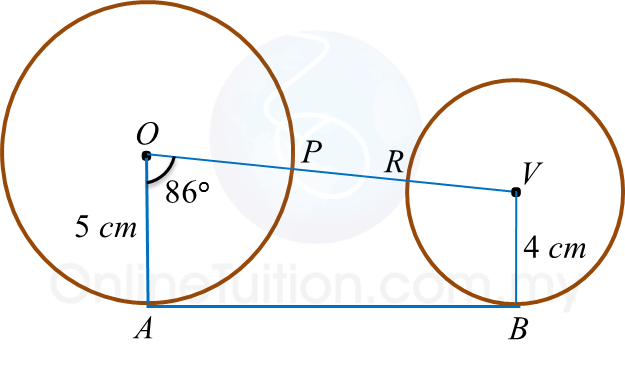
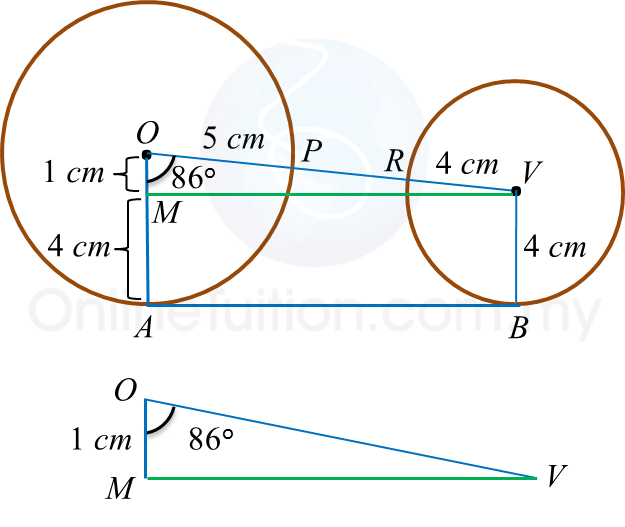
(a) BA = BC

(b)

∠

ABO =

∠

CBO = x^o

(c)

∠

AOB =

∠

COB = y^o

(d) ∠ OAB =

∠

OCB = 90^o

(e)

∠

AOC +

∠

ABC = 180^o

(f) ∆ AOB and ∆ COB are congruent