5.1 Gradient of a Straight Line

Posted on April 23, 2020 by user

5.1 Gradient of a Straight Line

The gradient of a straight line is the ratio of the vertical distance to the horizontal distance between any two given points on the straight line.

Gradient, m = \frac{Vertical distance}{Horizontal distance}

Example:

Find the gradient of the straight line above.

Solution:

\begin{array}{l} Gradient, m = \frac{Vertical distance}{Horizontal distance} \\ = \frac{4 units}{6 units} \\ = \frac{2}{3} \end{array}

5.2 Gradient of a Straight Line in Cartesian Coordinates (Sample Questions)

Posted on April 23, 2020 by user

Example 1:

Given that a straight line passes through points (-3, -7) and (4, 14). What is the gradient of the straight line?

Solution:

Let (x₁, y₁) = (-3, -7) and (x₂, y₂) = (4, 14).

Gradient of the straight line

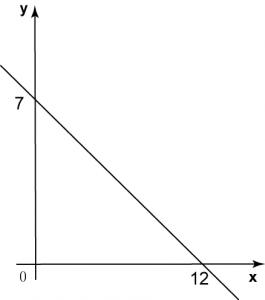
\begin{array}{l} = \frac{y_{2} - y_{1}}{x_{2} - x_{1}} \\ = \frac{14 - (- 7)}{4 - (- 3)} \\ = \frac{21}{7} = 3 \end{array}

Example 2:

The gradient of the straight line PQ in the diagram above is

Solution:

Let (x₁, y₁) = (12, 0) and (x₂, y₂) = (0, 7).

Gradient of the straight line PQ

\begin{array}{l} = \frac{y_{2} - y_{1}}{x_{2} - x_{1}} \\ = \frac{7 - 0}{0 - 12} \\ = - \frac{7}{12} \end{array}

Example 3:

A straight line with gradient -3 passes through points (-4, 6) and (-1, p). Find the value of p.

Solution:

\begin{array}{l} \frac{y_{2} - y_{1}}{x_{2} - x_{1}} = - 3 \\ \frac{p - 6}{- 1 - (- 4)} = - 3 \\ \frac{p - 6}{3} = - 3 \\ p - 6 = - 9 \\ p = - 3 \end{array}

5.4 Equation of a Straight Line (Sample Questions)

Posted on April 23, 2020 by user

Example 1:

Given that the equation of a straight line is 4x + 6y – 3 = 0. What is the gradient of the line?

Solution:

4x + 6y – 3 = 0

6y = – 4x + 3

\begin{array}{l} y = - \frac{4 x}{6} + \frac{3}{6} \\ y = - \frac{2}{3} x + \frac{1}{2} \\ y = m x + c \\ g r a d i e n t, m = - \frac{2}{3} \end{array}

Example 2:

Given that the equation of a straight line is y = – 7x + 3. Find the y-intercept of the line?

Solution:

y = mx + c, c is y-intercept of the straight line.

Therefore for the straight line y = – 7x + 3,

y-intercept is 3

Example 3:

Find the equation of the straight line MN if its gradient is equal to 3.

Solution:

Given m = 3

Substitute m = 3 and (-2, 5) into y = mx + c.

5 = 3 (-2) + c

5 = -6 + c

c = 11

Therefore the equation of the straight line MN is y = 3x + 11

5.4 Equation of a Straight Line

Posted on April 23, 2020 by user

5.4 Equation of a Straight Line: y = mx + c

1. Given the value of the gradient, m, and the y-intercept, c, an equation of a straight line
y = mx + c can be formed.

2. If the equation of a straight line is written in the form y = mx + c, the gradient, m, and the y-intercept, c, can be determined directly from the equation.

Example:

Given that the equation of a straight line is y = 3 – 4x. Find the gradient and y-intercept of the line?

Solution:

y= 3 – 4x

y= – 4x + 3 ← (y = mx + c)

Therefore, gradient, m = – 4

y-intercept, c = 3

3. If the equation of a straight line is written in the form ax + by + c = 0, change it to the form y = mx + c before finding the gradient and the y-intercept.

Example:

Given that the equation of a straight line is 4x + 6y– 3 = 0. What is the gradient and y-intercept of the line?

Solution:

4x + 6y – 3 = 0

6y = –4x + 3

\begin{array}{l} y = - \frac{2}{3} x + \frac{1}{2} \leftarrow y = m x + c \\ ∴ Gradient m = - \frac{2}{3} \\ y - intercept, c = \frac{1}{2} \end{array}

5.6 SPM Practice (Short Questions)

Posted on April 23, 2020 by user

Question 1:

Diagram below shows a straight line RS on a Cartesian plane.

Find the gradient of RS.

Solution:

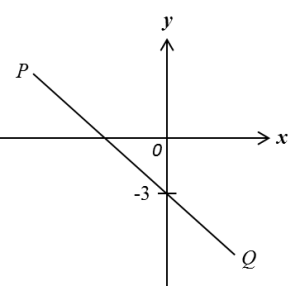
\begin{array}{l} Using gradient formula \frac{y_{2} - y_{1}}{x_{2} - x_{1}} \\ Gradient of R S = \frac{3 - 1}{5 - (- 1)} = \frac{2}{6} = \frac{1}{3} \end{array}

Question 2:

In diagram below, PQ is a straight line with gradient

- \frac{1}{2}

Find the x-intercept of the straight line PQ.

Solution:

\begin{array}{l} Using the gradient formula, m = - \frac{y-intercept}{x-intercept} \\ - \frac{1}{2} = - (\frac{- 3}{x-intercept}) \\ x-intercept = 3 \times (- 2) = - 6 \end{array}

Question 3:

Diagram below shows a straight line RS drawn on a Cartesian plane.

It is given that the distance of RS is 10 units.

Find the gradient of RS.

Solution:

\begin{array}{l} R S = 10 units, O S = 6 units \\ O R = \sqrt{10^{2} - {(- 6)}^{2}} = 8 units \\ y-intercept of R S = - 6 \\ x-intercept of R S = - 8 \\ Using the gradient formula, m = - \frac{y-intercept}{x-intercept} \\ ∴ Gradient of R S = - (\frac{- 6}{- 8}) = - \frac{3}{4} \end{array}

Question 4:

The gradient of the straight line 3x – 4y = 24 is

Solution:

Rearrange the equation in the form y = mx+ c

3x – 4y = 24

4y = 3x – 24

y = \frac{3}{4} x - 6

Therefore, gradient of the straight line =

\frac{3}{4} .

Question 5:

Determine the y-intercept of the straight line 3x + 2y = 5

Solution:

For y-intercept, x = 0

3(0) + 2y = 5

\begin{array}{l} y = \frac{5}{2} \\ ∴ y -intercept = \frac{5}{2} . \end{array}

5.7 SPM Practice (Long Questions 1)

Posted on April 23, 2020 by user

Question 1:

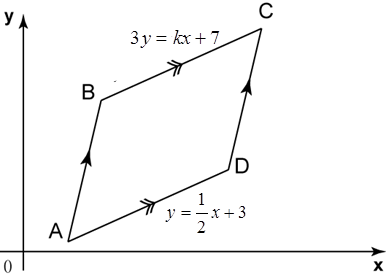
In diagram below, ABCD is a trapezium drawn on a Cartesian plane. BC is parallel to AD and O is the origin. The equation of the straight line BC is 3y = kx+ 7 and the equation of the straight line AD is

y = \frac{1}{2} x + 3

Find

(a) the value of k,

(b) the x-intercept of the straight line BC.

Solution:
(a)

Equation of BC :

3y = kx + 7

\begin{array}{l} y = \frac{k}{3} x + \frac{7}{3} \\ ∴ Gradient of B C = \frac{k}{3} \\ Equation of A D : y = \frac{1}{2} x + 3 \\ ∴ Gradient of A D = \frac{1}{2} \\ Gradient of B C = gradient of A D \\ \frac{k}{3} = \frac{1}{2} \\ ∴ k = \frac{3}{2} \end{array}

Gradient of BC = gradient of AD

\begin{array}{l} \frac{k}{3} = \frac{1}{2} \\ ∴ k = \frac{3}{2} \end{array}

(b)
Equation of BC,

3 y = \frac{3}{2} x + 7

For x-intercept, y = 0

\begin{array}{l} 3 (0) = \frac{3}{2} x + 7 \\ \frac{3}{2} x = - 7 \\ x = - \frac{14}{3} \end{array}

Therefore x-intercept of BC =

- \frac{14}{3}

Question 2:

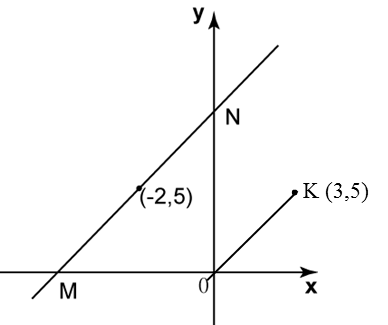
In diagram below, O is the origin. Straight line MN is parallel to a straight line OK.

Find

(a) the equation of the straight line MN,

(b) the x-intercept of the straight line MN.

Solution:

(a)
Gradient of MN = gradient of OK

Gradient of MN

\begin{array}{l} = \frac{5 - 0}{3 - 0} \\ = \frac{5}{3} \end{array}

Substitute m = 5/3 and (–2, 5) into y = mx + c

5 = \frac{5}{3} (- 2) + c

15 = – 10 + 3c

3c = 25

c = 25/3

Therefore equation of MN:

y = \frac{5}{3} x + \frac{25}{3}

(b)

For x-intercept, y = 0

\begin{array}{l} 0 = \frac{5}{3} x + \frac{25}{3} \\ \frac{5}{3} x = - \frac{25}{3} \end{array}

5x = –25

x = –5

Therefore x-intercept of MN = –5

5.3 Intercepts (Sample Questions)

Posted on April 23, 2020 by user

Example 1:

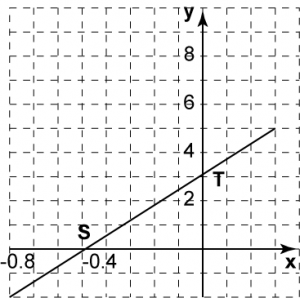
The x-intercept of the line ST is

Solution:

The x-coordinate for the point of intersection of the straight line with x-axis is -0.4.

Therefore the x-intercept of the line ST is –0.4.

Example 2:

Find the x-intercept of the straight line 2x + 3y + 6 = 0.

Solution:

2x + 3y + 6 = 0

At x-intercept, y = 0

2x + 3(0) + 6 = 0

2x = –6

x = –3

Example 3:

What is the y-intercept of the straight line 12x – 15y = 60?

Solution:

12x – 15y = 60

At y-intercept, x = 0

12(0) – 15y = 60

– 15y = 60

y = –4

5.5 Parallel Lines (Sample Questions)

Posted on April 23, 2020 by user

Example 1:

The straight lines MN and PQ in the diagram above are parallel. Find the value of q.

Solution:

If two lines are parallel, their gradients are equal.

m₁ = m₂

m_MN = m_PQ

\begin{array}{l} using gradient formula \frac{y_{2} - y_{1}}{x_{2} - x_{1}} \\ \frac{9 - 4}{5 - (- 1)} = \frac{q - (- 5)}{5 - (- 7)} \\ \frac{5}{6} = \frac{q + 5}{12} \end{array}

60 = 6q + 30

6q = 30

q = 5

5.5 Parallel Lines (Part 1)

Posted on April 23, 2020 by user

5.5 Parallel Lines (Part 1)

(A) Gradient of parallel lines

1. Two straight lines are
parallel if they have
the same gradient.

If PQ // RS,

then m_PQ = m_RS

2. If two straight lines have

the same gradient, then

they are parallel.

If m_AB = m_CD

then AB // CD

Example 1:

Determine whether the two straight lines are parallel.

(a) 2y – 4x = 6

y = 2x – 5

(b) 2y = 3x –4

3y = 2x +12

Solution:

(a)

2y – 4x = 6

2y = 6 + 4x

y = 2x + 3, m₁= 2

y = 2x – 5, m₂ = 2

m₁= m₂

Therefore, the two straight lines are parallel.

(b)

\begin{array}{l} 2 y = 3 x - 4 \\ y = \frac{3}{2} x - 2, m_{1} = \frac{3}{2} \\ 3 y = 2 x + 12 \\ y = \frac{2}{3} x + 4, m_{2} = \frac{2}{3} \\ m_{1} \neq m_{2} \\ ∴ The two straight lines are not parallel . \end{array}

5.6 SPM Practice (Short Questions)

Posted on April 23, 2020 by user

5.6.2 The Straight Line, SPM Paper 1 (Short Questions)

Question 6:

Diagram below shows a straight line RS with equation 3y = –px – 12, where p is a constant.

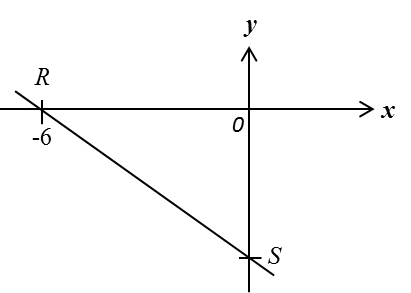
It is given that OR: OS = 3 : 2.

Find the value of p.

Solution:

Method 1:

Substitute x= –6 and y = 0 into 3y = –px – 12:

3(0) = –p (–6) – 12

0 = 6p – 12

–6p = –12

p = 2

Method 2:

OR: OS = 3 : 2

\begin{array}{l} \frac{O R}{O S} = \frac{3}{2} \\ \frac{6}{O S} = \frac{3}{2} \\ O S = 6 \times \frac{2}{3} = 4 units \end{array}

Coordinates of S = (0, –4)

Gradient of the straight line RS =

- \frac{- 4}{- 6} = - \frac{2}{3}

Given 3y = –px – 12
Rearrange the equation in the form y = mx + c

\begin{array}{l} y = - \frac{p}{3} x - 4 \\ Gradient of the straight line R S = - \frac{P}{3} \\ ∴ - \frac{P}{3} = - \frac{2}{3} \\ P = 2 \end{array}

Question 7:

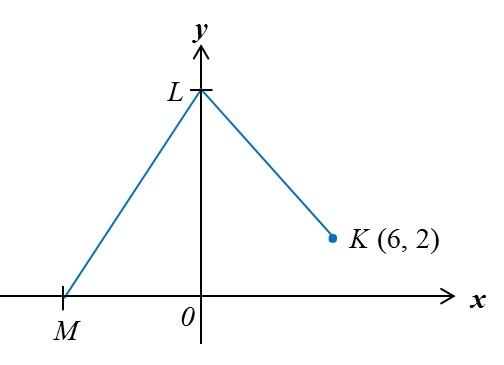
The above diagram shows two straight lines, KL and LM, on a Cartesian plane. The distance KL is 10 units and the gradient of LM is 2. Find the x-intercept of LM.

Solution:

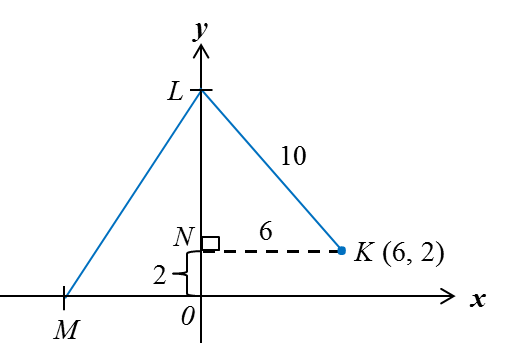
Let point N be = (0, 2).

Using Pythagoras’ Theorem,

LN = √10² – 6² = 8

Point L = (0, 2 + 8) = (0, 10)

y-intercept of LM = 10

\begin{array}{l} Using the gradient formula, m = - \frac{y-intercept}{x-intercept} \\ 2 = - (\frac{10}{x-intercept}) \\ x-intercept of L M = - \frac{10}{2} = - 5 \end{array}