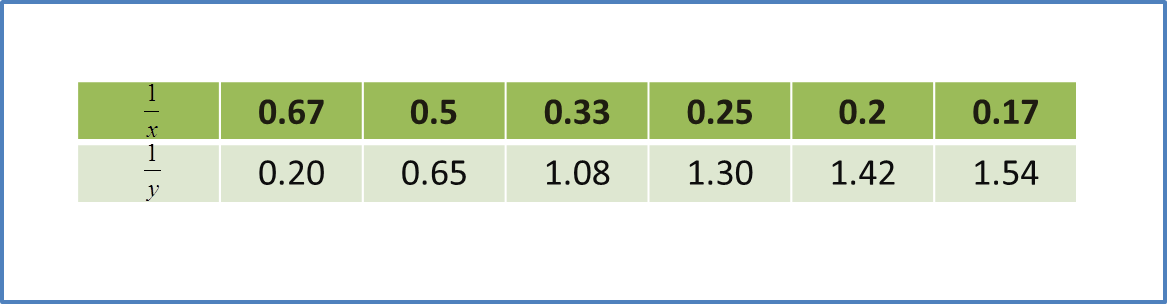
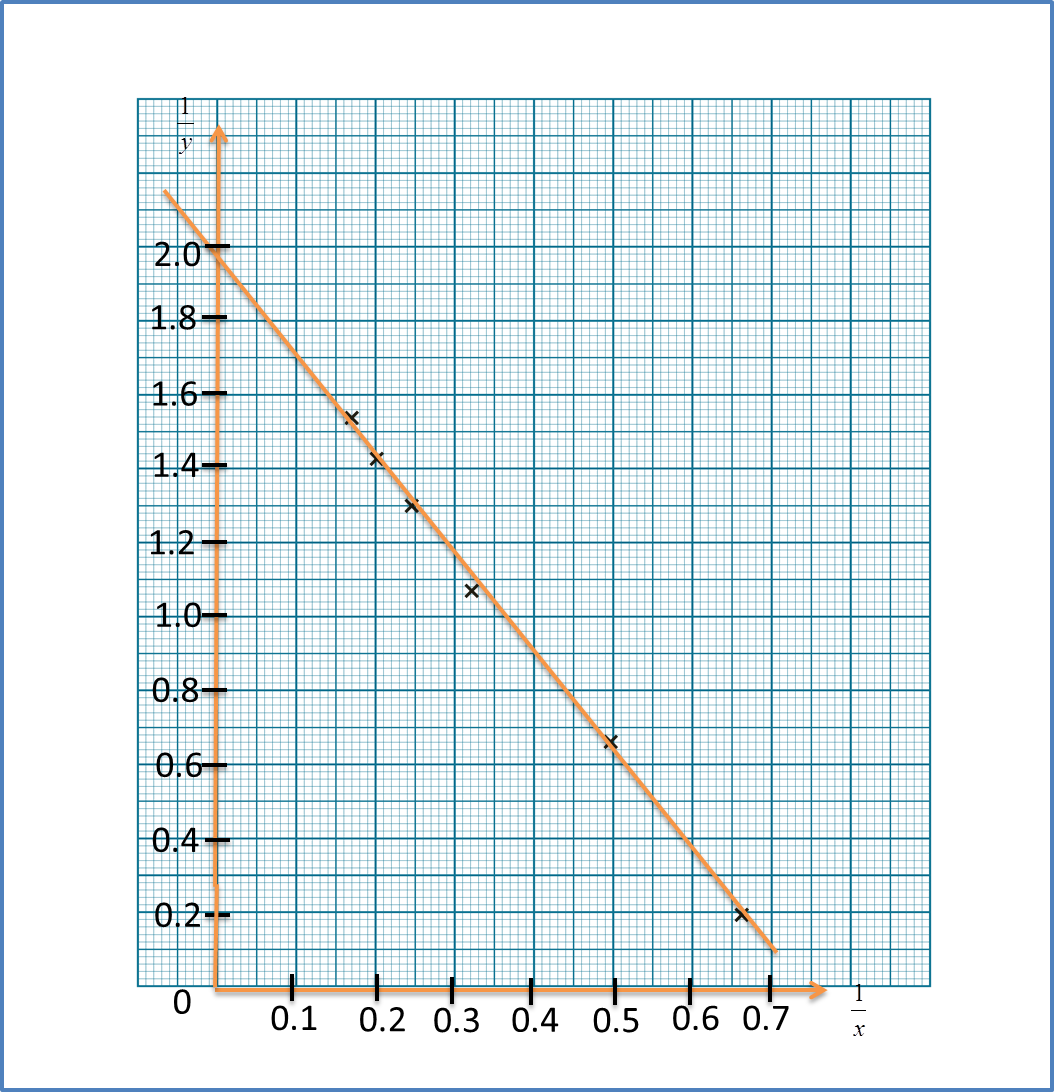
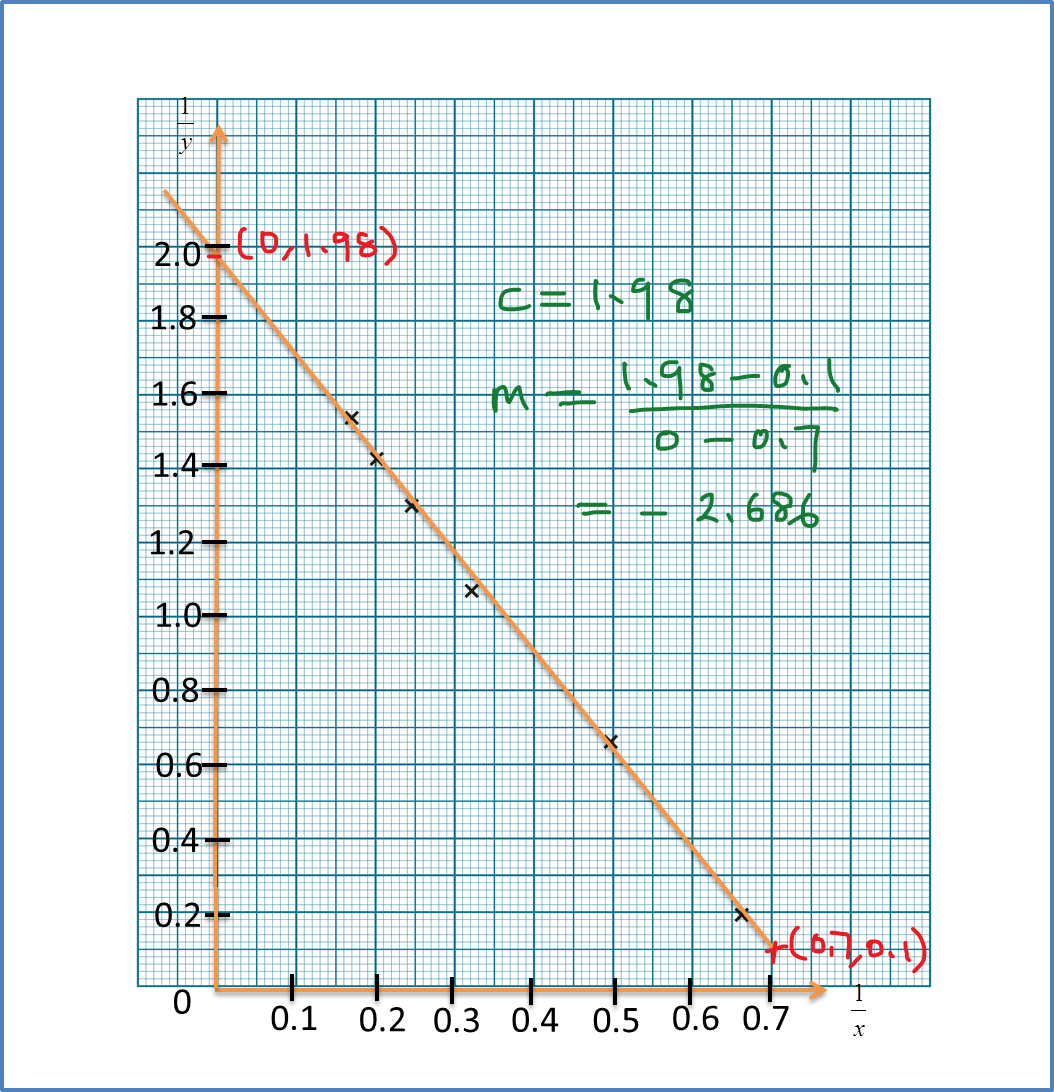
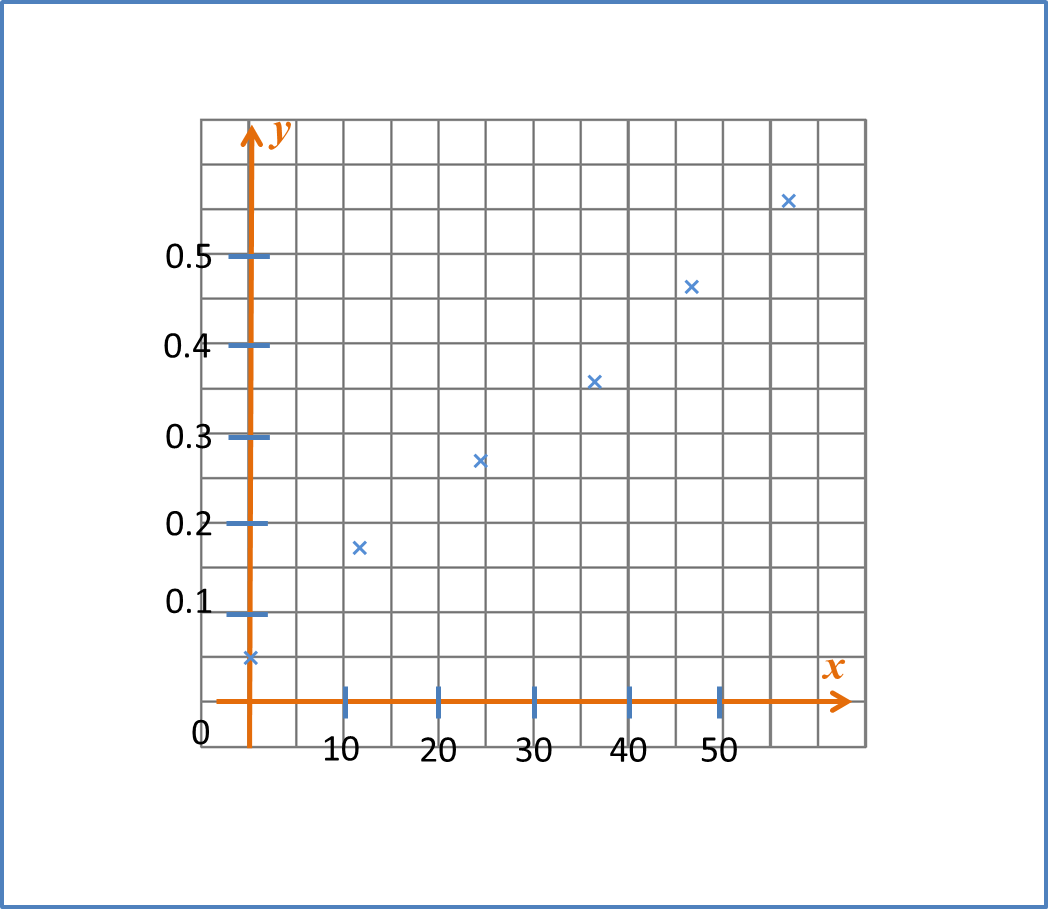
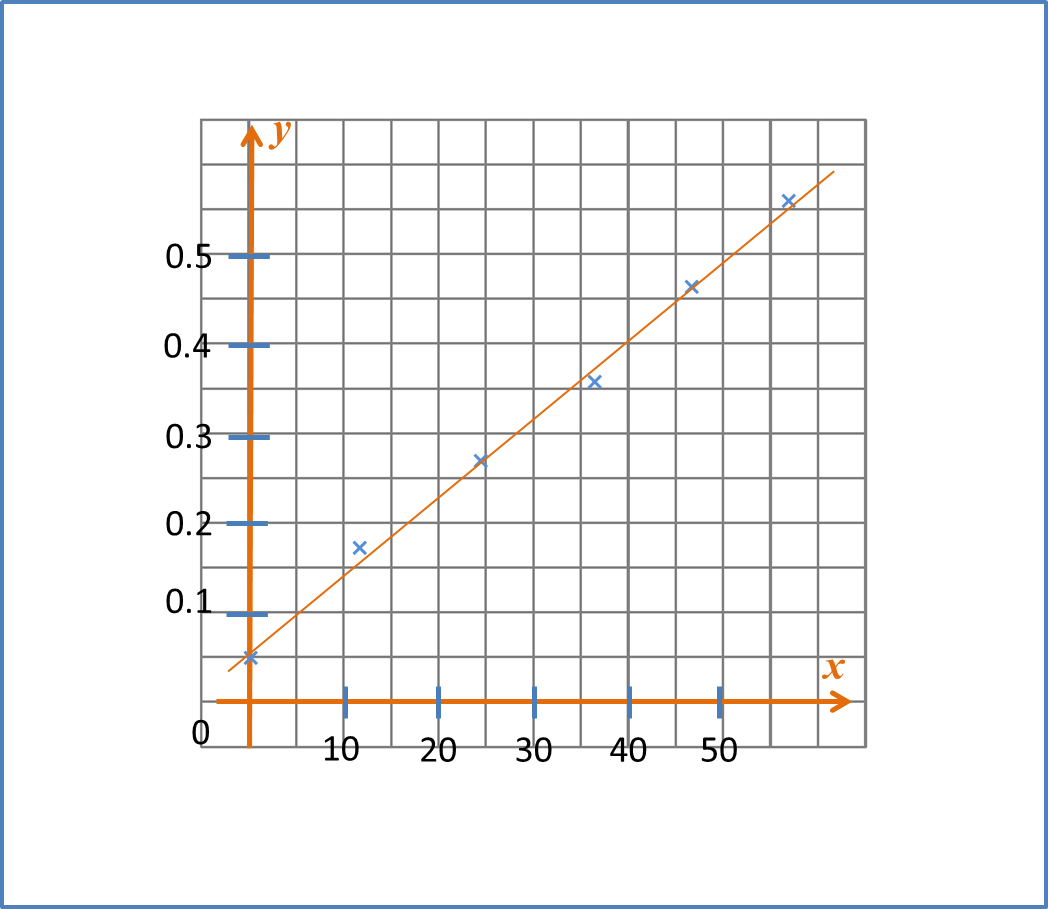
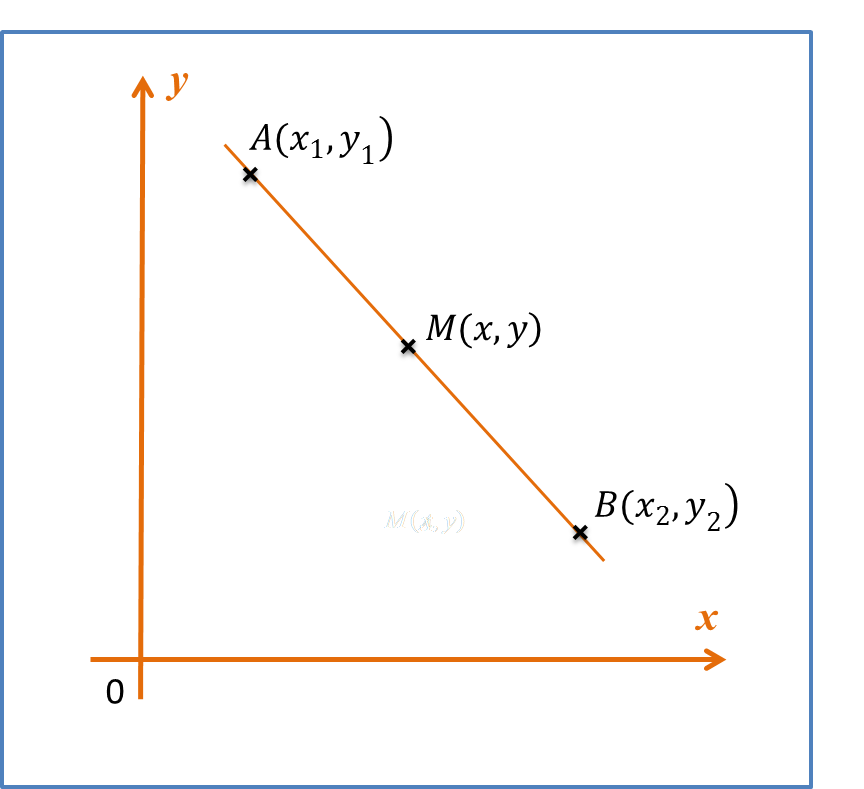
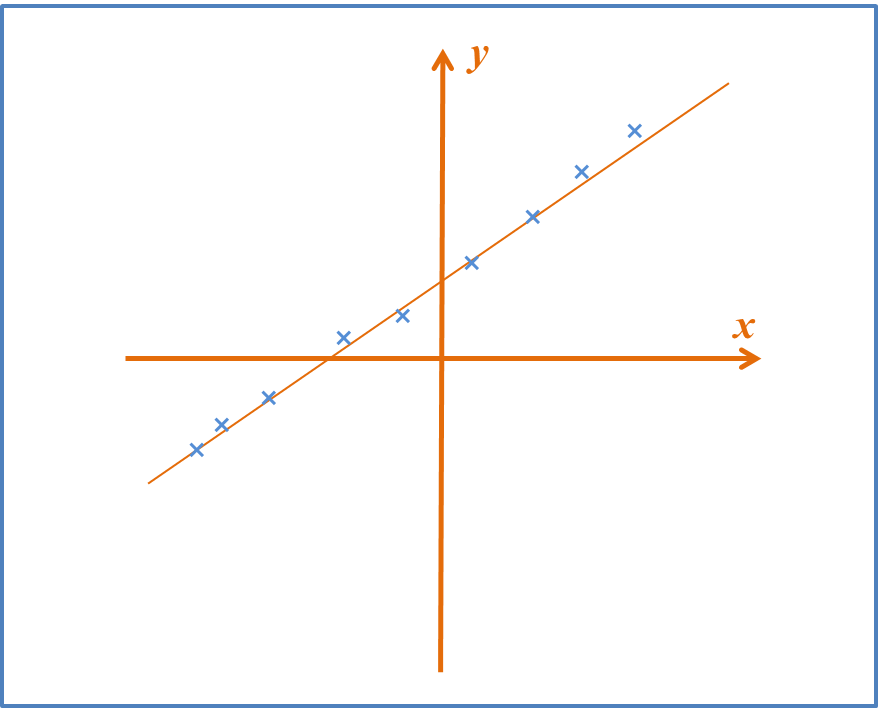
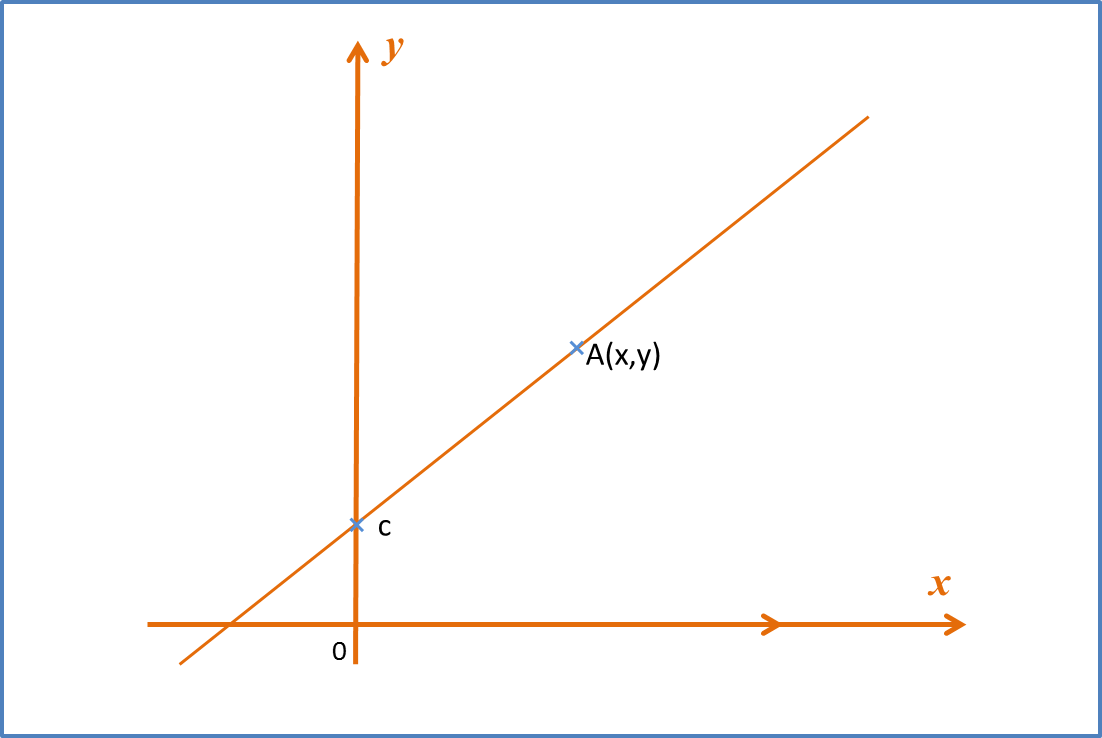
(B) Gradient of a Straight Line
If the points A(x1,y1) and B(x2,y2) lie on the straight line y=mx+c , then gradient of ,the straight line
m=y2−y1x2−x1ory1−y2x1−x2
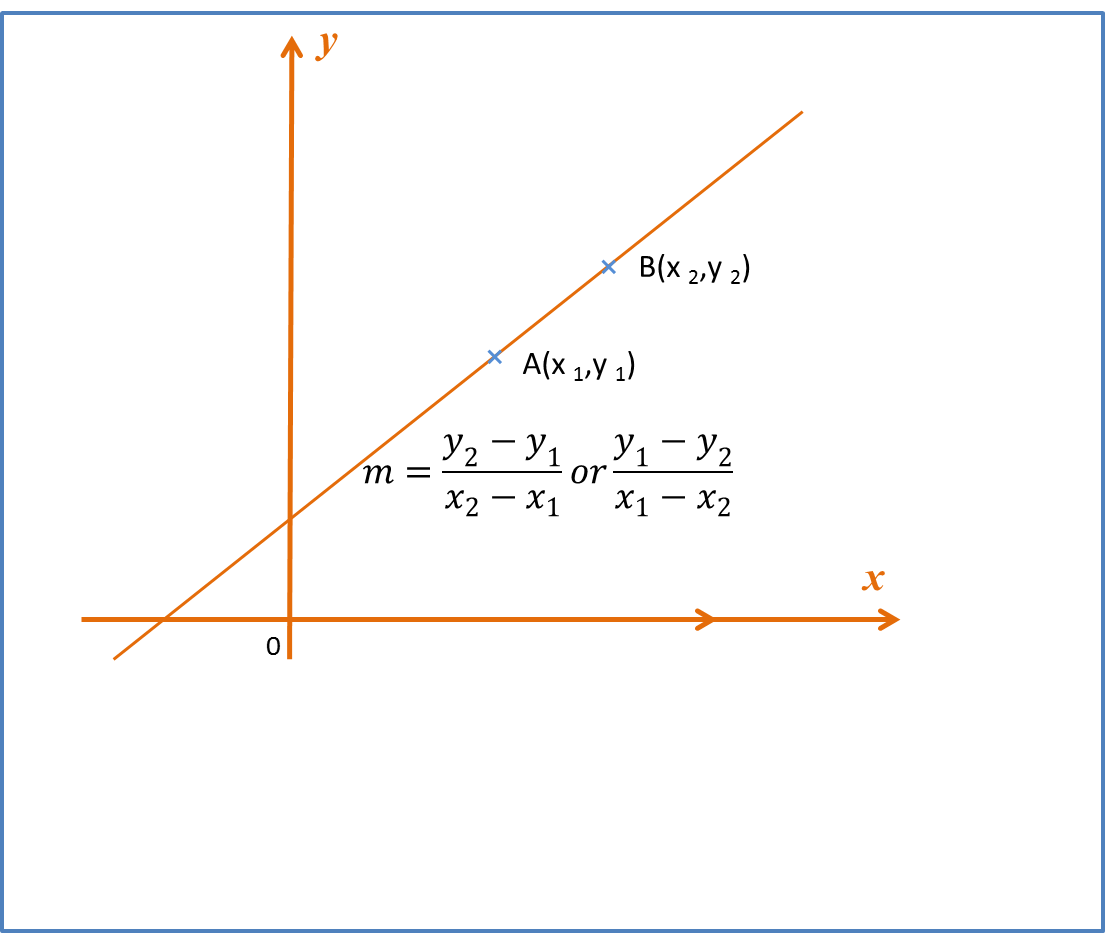
If the points A(x1,y1) and B(x2,y2) lie on the straight line y=mx+c , then gradient of ,the straight line
m=y2−y1x2−x1ory1−y2x1−x2