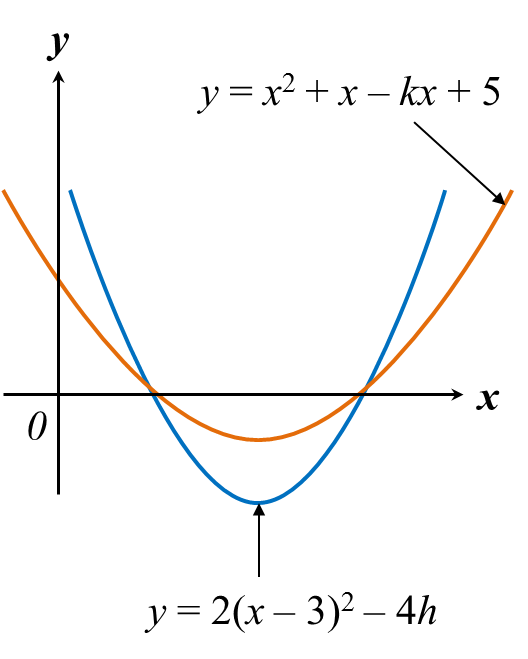
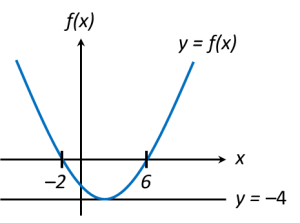
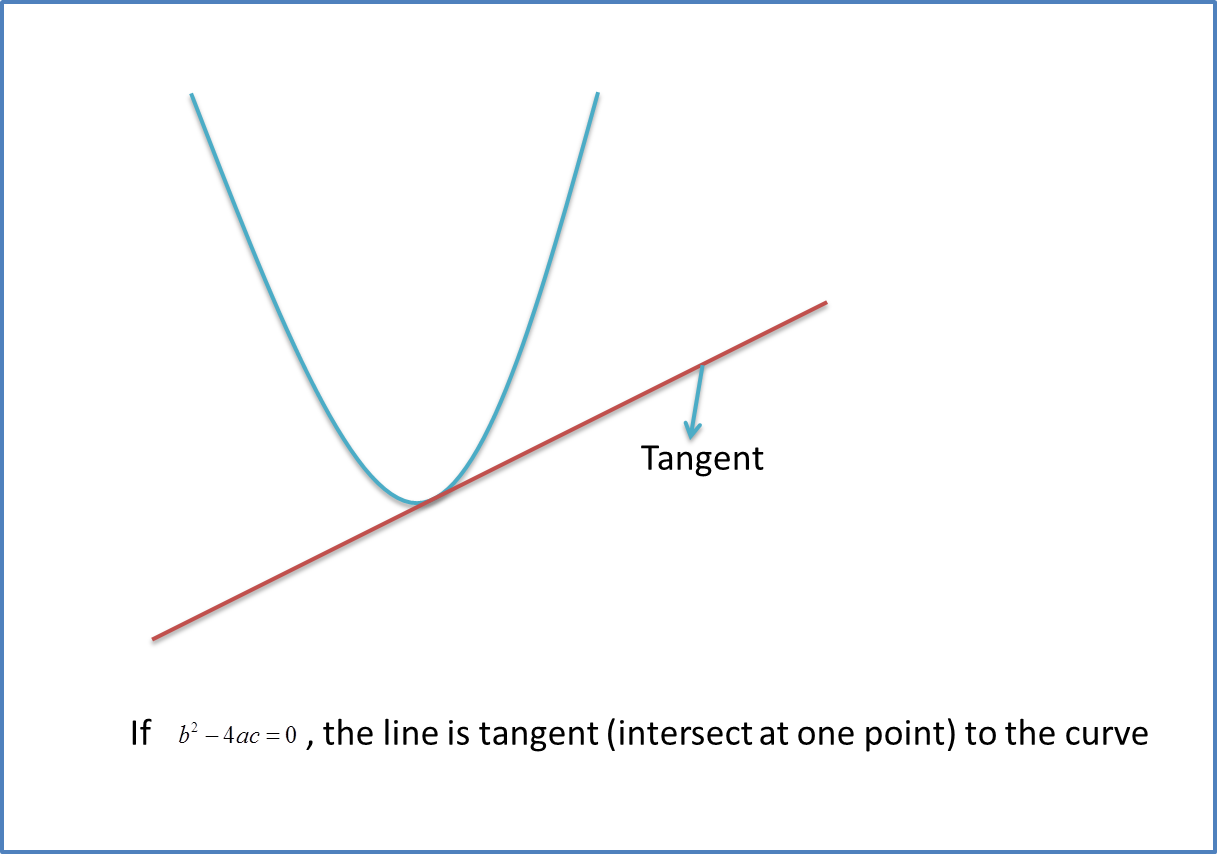
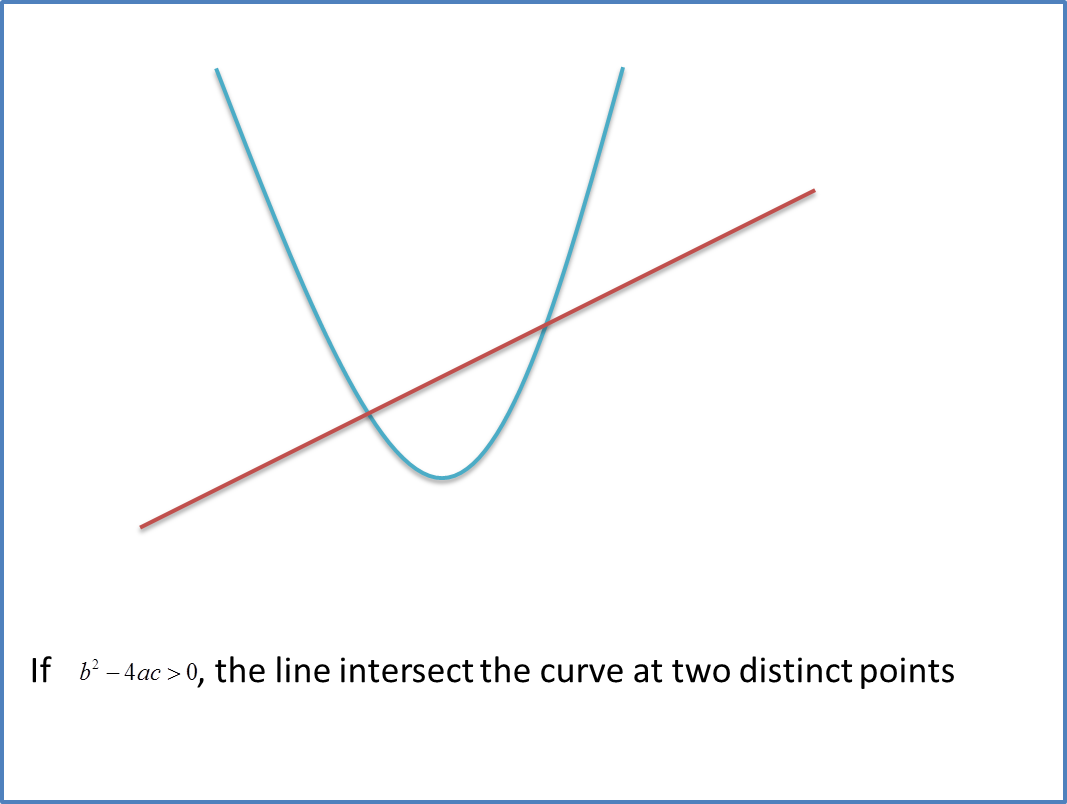
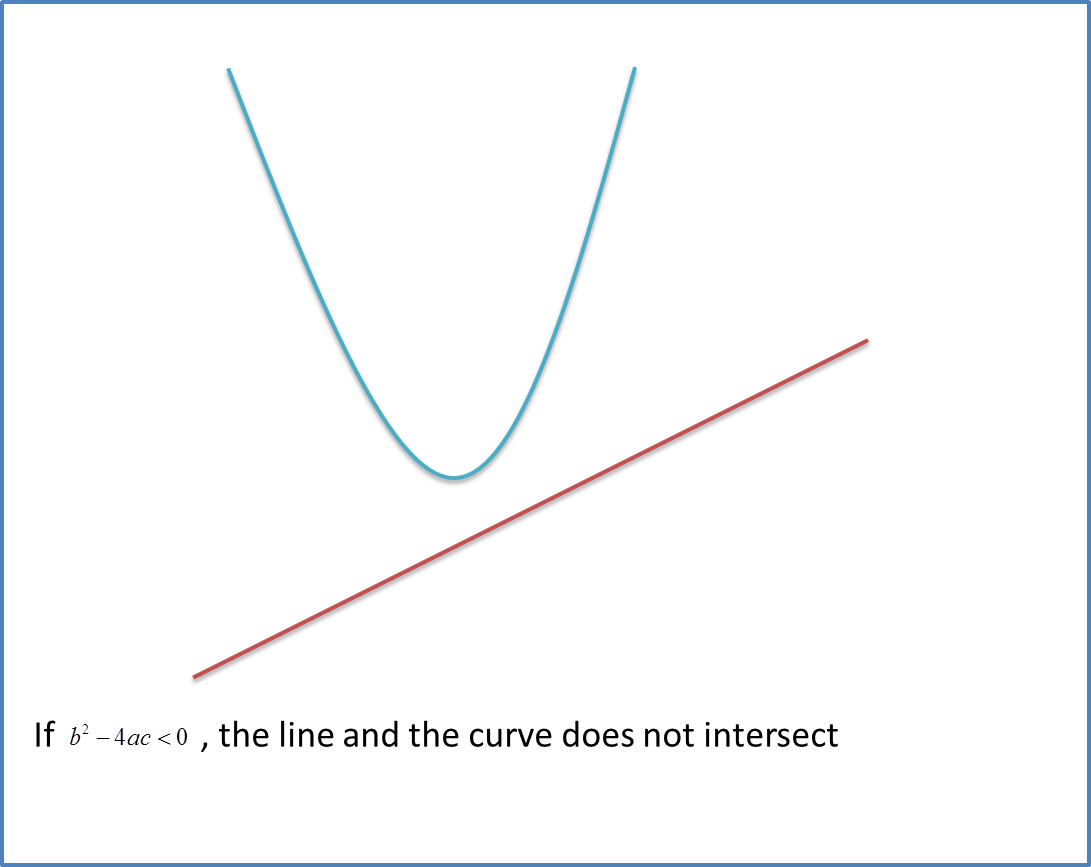
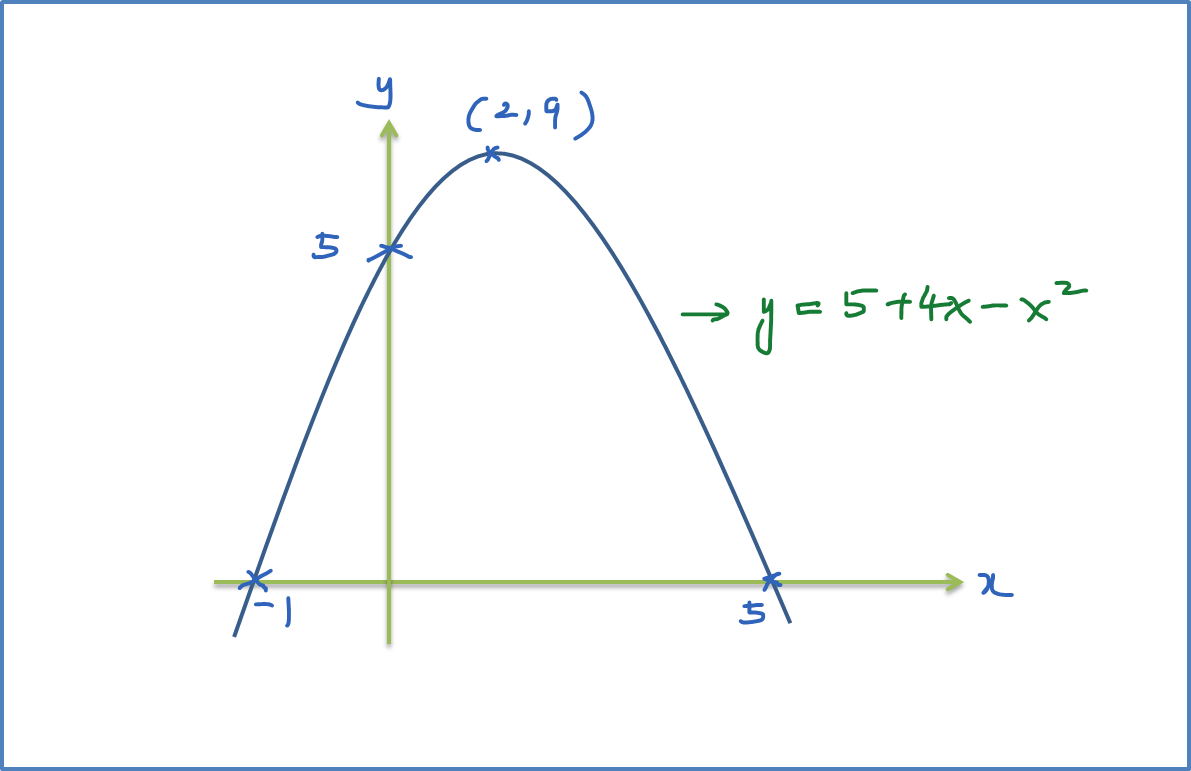
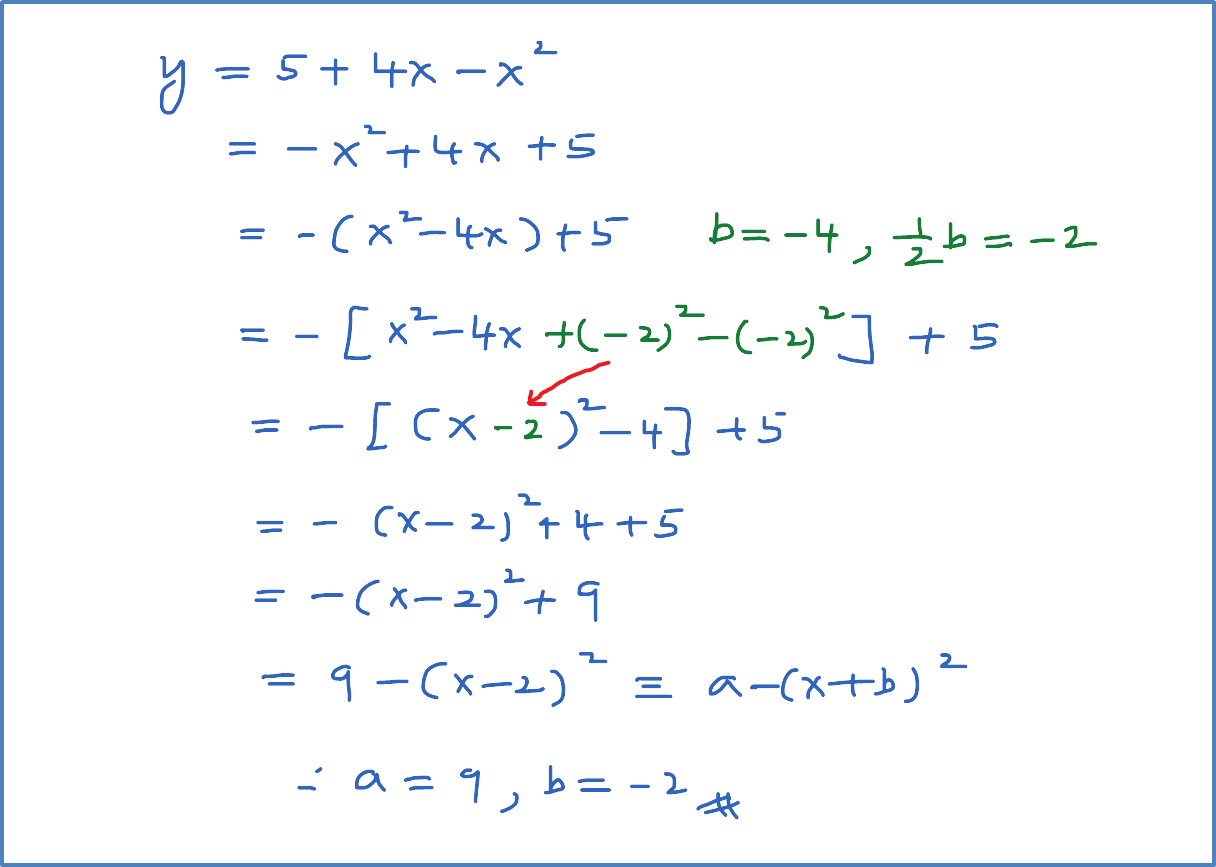Simultaneous Equations (Example 1 & 2)

Posted on April 18, 2020 by user

Example 1:

Solve the simultaneous equations.

$x + \frac{1}{4} y = 1 and y^{2} - 8 = 4 x .$

Solution:

$\begin{array}{l} x + \frac{1}{4} y = 1 \to (1) \\ y^{2} - 8 = 4 x \to (2) \\ x = 1 - \frac{1}{4} y \to (3) \end{array}$

Substitute (3) into (2),

$\begin{array}{l} y^{2} - 8 = 4 (1 - \frac{1}{4} y) \\ y^{2} - 8 = 4 - \frac{4}{4} y \end{array}$

y² + y – 12 = 0

(y + 4)(y – 3) = 0

y = –4 or y = 3

Substitute the values of y into (3),

$\begin{array}{l} when y = - 4, \\ x = 1 - \frac{1}{4} (- 4) = 2 \\ when y = 3, \\ x = 1 - \frac{1}{4} (3) = \frac{1}{4} \\ The solutions are x = 2, y = - 4 and x = \frac{1}{4}, y = 3 \end{array}$

Example 2:

Solve the simultaneous equations 2x + y = 1 and 2x²+ y² + xy = 5.

Correct your answer to three decimal places.

Solution:

2x + y = 1-----(1)

2x² + y²+ xy = 5-----(2)

From (1),

y = 1 – 2x-----(3)

Substitute (3) into (2).

2x² + (1 – 2x)² + x(1 – 2x) = 5

2x² + (1 – 2x)(1 – 2x) + x – 2x² = 5

1 – 2x – 2x + 4x² + x – 5 = 0

4x² – 3x – 4 = 0

$\begin{array}{l} From x = \frac{- b \pm \sqrt{b^{2} - 4 a c}}{2 a} \\ a = 4, b = - 3, c = - 4 \\ x = \frac{- (- 3) \pm \sqrt{{(- 3)}^{2} - 4 (4) (- 4)}}{2 (4)} \\ x = \frac{3 \pm \sqrt{73}}{8} \\ x = - 0.693 or 1.443 \end{array}$

Substitute the values of x into (3).

When x = –0.693,

y = 1 – 2 (–0.693) = 2.386 (correct to 3 decimal places)

When x = 1.443,

y = 1 – 2 (1.443) = –1.886 (correct to 3 decimal places)

The solutions are x = –0.693, y = 2.386 and x = 1.443, y = –1.886.

Quadratic Functions, SPM Practice (Long Questions)

Posted on April 18, 2020 by user

Question 5:

Diagram above shows the graphs of the curves y = x² + x – kx + 5 and y = 2(x – 3) – 4h that intersect the x-axis at two points. Find
(a) the value of k and of h,
(b) the minimum value of each curve.

Solution:
(a)

$\begin{array}{l} y = x^{2} + x - k x + 5 \\ = x^{2} + (1 - k) x + 5 \\ = {[x + \frac{(1 - k)}{2}]}^{2} - {(\frac{1 - k}{2})}^{2} + 5 \\ axis of symmetry of the graph is \\ x = - \frac{(1 - k)}{2} \end{array}$

$\begin{array}{l} y = 2 {(x - 3)}^{2} - 4 h \\ axis of symmetry of the graph is x = 3. \\ ∴ - \frac{1 - k}{2} = 3 \\ - 1 + k = 6 \\ k = 7 \end{array}$

$\begin{array}{l} Substitute k = 7 into equation \\ y = x^{2} + x - 7 x + 5 \\ = x^{2} - 6 x + 5 \\ At x -axis, y = 0; \\ x^{2} - 6 x + 5 = 0 \\ (x - 1) (x - 5) = 0 \\ x = 1, 5 \end{array}$

$\begin{array}{l} At point (1, 0) \\ Substitute x = 1, y = 0 into the graph: \\ y = 2 {(x - 3)}^{2} - 4 h \\ 0 = 2 {(1 - 3)}^{2} - 4 h \\ 4 h = 2 (4) \\ 4 h = 8 \\ h = 2 \end{array}$

(b)

$\begin{array}{l} For y = x^{2} - 6 x + 5 \\ = {(x - 3)}^{2} - 9 + 5 \\ = {(x - 3)}^{2} - 4 \\ ∴ Minimum value is - 4. \\ For y = 2 {(x - 3)}^{2} - 8, minimum value is - 8. \end{array}$

Quadratic Functions, SPM Practice (Long Questions)

Posted on April 18, 2020 by user

3.9.1 Quadratic Functions, SPM Practice (Long Questions)

Question 1:

Without drawing graph or using method of differentiation, find the maximum or minimum value of the function y = 2 + 4x – 3x². Hence, find the equation of the axis of symmetry of the graph.

Solution:

By completing the square for the function in the form of y = a(x + p)²+ q to find the maximum or minimum value of the function.

y = 2 + 4x – 3x²

y = – 3x²+ 4x + 2 ← (in general form)

$\begin{array}{l} y = - 3 [x^{2} - \frac{4}{3} x - \frac{2}{3}] \\ y = - 3 [x^{2} - \frac{4}{3} x + {(- \frac{4}{3} \times \frac{1}{2})}^{2} - {(- \frac{4}{3} \times \frac{1}{2})}^{2} - \frac{2}{3}] \\ y = - 3 [{(x - \frac{2}{3})}^{2} - {(- \frac{2}{3})}^{2} - \frac{2}{3}] \end{array}$

$\begin{array}{l} y = - 3 [{(x - \frac{2}{3})}^{2} - \frac{4}{9} - \frac{6}{9}] \\ y = - 3 [{(x - \frac{2}{3})}^{2} - \frac{10}{9}] \\ y = - 3 {(x - \frac{2}{3})}^{2} + \frac{10}{3} \leftarrow in the form of a {(x + p)}^{2} + q \end{array}$

Since a = –3 < 0,

Therefore, the function y has a maximum value of

$\frac{10}{3} .$

$\begin{array}{l} x - \frac{2}{3} = 0 \\ x = \frac{2}{3} \end{array}$

Equation of the axis of symmetry of the graph is

$x = \frac{2}{3} .$

Question 2:

The diagram above shows the graph of a quadratic function y = f(x). The straight line y = –4 is tangent to the curve y = f(x).

(a) Write the equation of the axis of symmetry of the function f(x).

(b) Express f(x) in the form of (x + p)² + q , where p and q are constant.

(i) f(x) < 0, (ii) f(x) ≥ 0.

Solution:

(a)

x-coordinate of the minimum point is the midpoint of (–2, 0) and (6, 0)

$= \frac{- 2 + 6}{2} = 2$

Therefore, equation of the axis of symmetry of the function f(x) is x = 2.

(b)

Substitute x = 2 into x + p = 0,

2 + p = 0

p = –2

and q = –4 (the smallest value of f(x))

Therefore, f(x) = (x + p)² + q

f(x) = (x – 2)² – 4

(c)(i) From the graph, for f(x) < 0, range of values of x are –2 < x < 6 ← (below x-axis).

(c)(ii) From the graph, for f(x) ≥ 0, range of values of x are x ≤ –2 or x ≥ 6 ← (above x-axis).

Quadratic Functions, SPM Practice (Short Questions)

Posted on April 18, 2020 by user

Question 5:
Find the range of values of k if the quadratic equation 3(x² – kx – 1) = k – k² has two real and distinc roots.

Solution:

$\begin{array}{l} 3 (x^{2} - k x - 1) = k - k^{2} \\ 3 x^{2} - 3 k x - 3 - k + k^{2} = 0 \\ 3 x^{2} - 3 k x + k^{2} - k - 3 = 0 \\ a = 3, b = - 3 k, c = k^{2} - k - 3 \\ In cases of two real and distinc roots, \\ b^{2} - 4 a c > 0 is applied . \\ {(- 3 k)}^{2} - 4 (3) (k^{2} - k - 3) > 0 \\ 9 k^{2} - 12 k^{2} + 12 k + 36 > 0 \\ - 3 k^{2} + 12 k + 36 > 0 \\ - k^{2} + 4 k + 12 > 0 \\ k^{2} - 4 k - 12 < 0 \\ (k + 2) (k - 6) < 0 \\ k = - 2, 6 \end{array}$

$The range of values of k is - 2 < k < 6.$

Question 6:
Given that the quadratic equation hx² – (h + 2)x – (h – 4) = 0 has real and distinc roots. Find the range of values of h.

Solution:

$\begin{array}{l} The quadratic equation h x^{2} - (h + 2) x - (h - 4) = 0 \\ has real and distinc roots . \\ b^{2} - 4 a c > 0 is applied . \\ {(- h - 2)}^{2} - 4 (h) (- h + 4) > 0 \\ h^{2} + 4 h + 4 + 4 h^{2} - 16 h > 0 \\ 5 h^{2} - 12 h + 4 > 0 \\ (5 h - 2) (h - 2) > 0 \\ The coefficient of h^{2} is positive, \\ the region above the x -axis should be shaded . \\ (5 h - 2) (h - 2) = 0 \\ h = \frac{2}{5}, 2 \end{array}$

$\begin{array}{l} The range of values of h for (5 h - 2) (h - 2) >0 is \\ h < \frac{2}{5} or h > 2. \end{array}$

3.5b Nature of the Roots (Combination of Straight Line and a Curve)

Posted on April 18, 2020 by user

Example 2 (Combination of Straight Line and a Curve)
The straight line

$y = 2 k + 1$ intersects the curve

$y = x + \frac{k^{2}}{x}$ at two distinct points. Find the range of values of k.

Example 3 (Straight Line does not intersect the curve)
Find the range of values of m for which the straight line

$y = m x + 6$ does not meet the curve

$2 x^{2} - x y = 3$ .

3.5a Nature of the Roots (Combination of Straight Line and a Curve)

Posted on April 18, 2020 by user

Example 1
Find the value of p for which

$8 y = x + 2 p$ is a tangent to the curve

$2 y^{2} = x + p$ .

3.5 Nature of the Roots (Combination of Straight Line and a Curve)

Posted on April 18, 2020 by user

Nature of the Roots (Combination of Straight Line and the Curve)
When you have a straight line and a curve, you can solve the equation of the straight line and the curve simultaneously and form a quadratic equation, ax² +bx + c = 0. The discriminant,

$b^{2} - 4 a c$ gives information about the number of points of intersection.

3.4 Quadratic Inequalities (Part 1)

Posted on April 18, 2020 by user

Solving Quadratic Inequality

The solution of the quadratic inequalities are the ranges of values which satisfied the inequalities itself.
There are 2 methods to solve the inequalities.

Graph method
Number line method

Step to solve a Quadratic Inequalities
Step 1 : Rewrite the inequality with zero on one side and make sure a > 0
Step 2 : Find where it crosses the x-axis (Put y = 0)
Step 3 : Sketch the graph and shade the region to find the range of values of x

Example
Find the range of values of x for each of the following :
(a)

$x^{2} - 4 x + 3 < 0$
(b)

$12 + 10 x - 2 x^{2} < 0$

Revision - Linear Inequality

Solving Quadratic Inequality - Graph Method

Solving Quadratic Inequality - Number Line Method

3.3c Sketching the Graph of Quadratic Functions (Example)

Posted on April 18, 2020 by user

Example 1
Express

$y = 5 + 4 x - x^{2}$ in the form

$y = a - {(x + b)}^{2}$ , where a, b, and c are constants. Hence state the maximum value of y and the value of x at which it occurs. Sketch the curve

$y = 5 + 4 x - x^{2}$ .

3.3b Sketching the Graph of Quadratic Functions

Posted on April 18, 2020 by user

Graphing Quadratic Function

If you are asked to sketch the graph of a quadratic function, you need to show
a. the shape of the graph
b. the maximum/minimum point of the graph
c. the x-intercept of the graph
d. the y-intercept of the graph

Example
Sketch the curve of the quadratic function

$f (x) = x^{2} - x - 12$

Answer:
The shape of the graph
Since the coefficient of x² is positive, hence the graph is a U shape parabola with a minimum point.

The minimum point of the graph
By completing the square

$\begin{array}{l} f (x) = x^{2} - x - 12 \\ f (x) = x^{2} - x + {(\frac{1}{2})}^{2} - {(\frac{1}{2})}^{2} - 12 \\ f (x) = {(x - \frac{1}{2})}^{2} - \frac{1}{4} - 12 \\ f (x) = {(x - \frac{1}{2})}^{2} - 12 \frac{1}{4} \\ Minimum point = (\frac{1}{2}, - 12 \frac{1}{4}) \end{array}$

For y-intercept, x = 0

$f (0) = (0)^{2} - (0) - 12 = - 12$

For x-intercept, f(x) = 0

$\begin{array}{l} f (x) = x^{2} - x - 12 \\ 0 = x^{2} - x - 12 \\ (x + 5) (x - 6) = 0 \\ x = - 5 or x = 6 \end{array}$

SPM Add Maths

Simultaneous Equations (Example 1 & 2)

Quadratic Functions, SPM Practice (Long Questions)

Quadratic Functions, SPM Practice (Long Questions)

Quadratic Functions, SPM Practice (Short Questions)

3.5b Nature of the Roots (Combination of Straight Line and a Curve)

3.5a Nature of the Roots (Combination of Straight Line and a Curve)

3.5 Nature of the Roots (Combination of Straight Line and a Curve)

3.4 Quadratic Inequalities (Part 1)

Solving Quadratic Inequality

Revision - Linear Inequality

Solving Quadratic Inequality - Graph Method

Solving Quadratic Inequality - Number Line Method

Suggested Video

3.3c Sketching the Graph of Quadratic Functions (Example)

3.3b Sketching the Graph of Quadratic Functions

Suggested Video