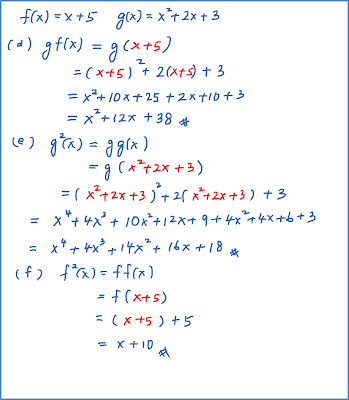Finding a new function given a composite function (Case B : Second function is given) Example 1

Posted on April 18, 2020 by user

Example 1 (substitution Method)
A function f is defined by

$f : x \mapsto x + 2$ .
Find the function g if

$g f : x \mapsto x^{2} + 3 x + 5$ .

[Note : Second function is given, use substitution y = x + 2]

Finding a new function given a composite function (Case A : First function is given) Example 3

Posted on April 18, 2020 by user

Example 3
A function f is defined by

$f : x \mapsto 2 x + 1$ .
Find the function g if

$f g : x \mapsto \frac{5 x - 2}{x + 5}, x \neq - 5$ .

[Note : First function is given]

Click here (check for example 5)

Finding a new function given a composite function (Case A : First function is given) Example 2

Posted on April 18, 2020 by user

Example 2
A function f is defined by

$f : x \mapsto \frac{2}{x}$ .
Find the function g if

$f g : x \mapsto x^{2} + 1$ .

[Note : the first function f is given]

Click here (check for example 5)

Finding a new function given a composite function (Case A : First function is given) Example 1

Posted on April 18, 2020 by user

Example 1
A function f is defined by

$f : x \mapsto 2 x + 5$ .
Find the function g if

$f g : x \mapsto 3 x - 8$ .

[Note : First function f is given]

Click here (check for example 5) to learn more about function

Composite Function (Comparison Method) Example 2

Posted on April 18, 2020 by user

Example 2
Given

$f : x \mapsto 1 - x$ and

$g : x \mapsto p x^{2} + q$ . If the composite function gf is defined by

$g f : x \mapsto 3 x^{2} - 6 x + 5$ , find
(a) the value of p and of q,
(b) the value of

$g^{2} (- 1)$ .

Composite Function (Comparison Method) Example 1

Posted on April 18, 2020 by user

Example 1
Given

$f : x \mapsto h x + k, g : x \mapsto {(x + 1)}^{2} + 4$ and

$f g : x \mapsto 2 {(x + 1)}^{2} + 5.$ Find
(a) the value of g²(2),
(b) the value of h and of k.

Example 3

Posted on April 18, 2020 by user

Example 3

If

$f : x \mapsto 2 x + 1$ and

$g : x \mapsto \frac{5}{x}, x \neq 0$ . Find the composite functions gf , fg and the value of gf(4).

Example 2

Posted on April 18, 2020 by user

Given $f : x \mapsto 1 - x$ and $g : x \mapsto p x^{2} + q$ . If the composite function gf is defined by $g f : x \mapsto 3 x^{2} - 6 x + 5$ , find

the value of p and of q,
the value of $g^{2} (- 1)$ .

Example 2

Posted on April 18, 2020 by user

Example 2

Functions f and g are defined by

$f : x \mapsto x - 1$ and

$g : x \mapsto \frac{3 - x}{x + 4}$ . Find
(a) the value of gf(3),
(b) the value of fg(-1 ),
(c) the composite functions fg,
(d) the composite functions gf,
(e) the composite functions g²,
(f) the composite functions f².

Example 1

Posted on April 18, 2020 by user

If f : x → x + 5 and g : x → x² +2x + 3, find

the value of gf (2),
the value of fg (2 ),
the composite functions fg,
the composite functions gf,
the composite functions g² ,
the composite functions f².

correction for part (c)

$\begin{array}{l} f g (x) = f (x^{2} + 2 x + 3) \\ = (x^{2} + 2 x + 3) + 5 \\ = x^{2} + 2 x + 3 + 5 \\ = x^{2} + 2 x + 8 \end{array}$