Home › SPM Maths › Archive for Earth as a Sphere › Page 2

Earth as a Sphere

9.4.3 Shortest Distance between Two Points

Posted on by

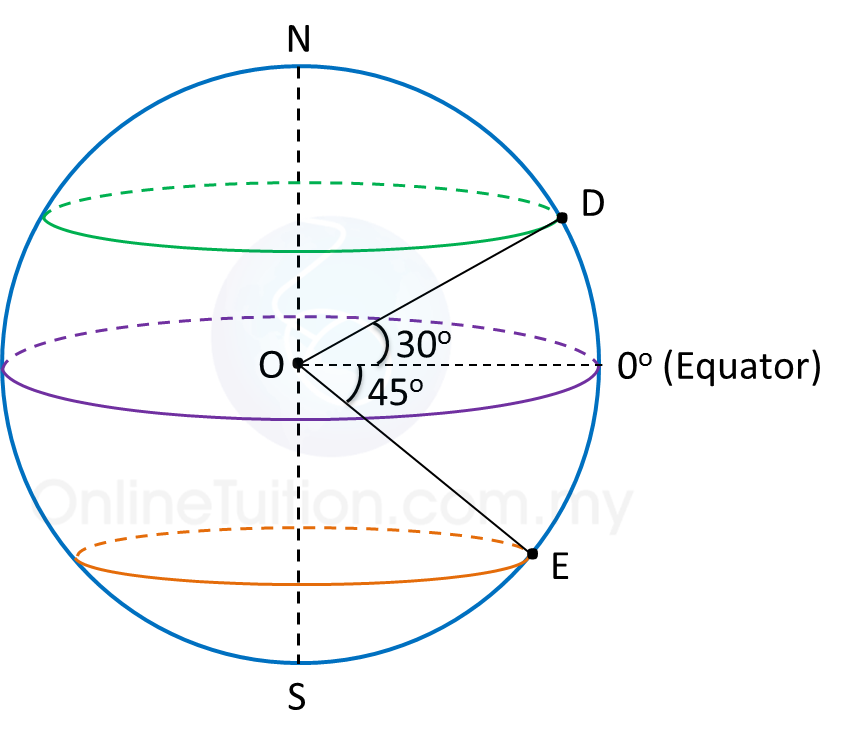
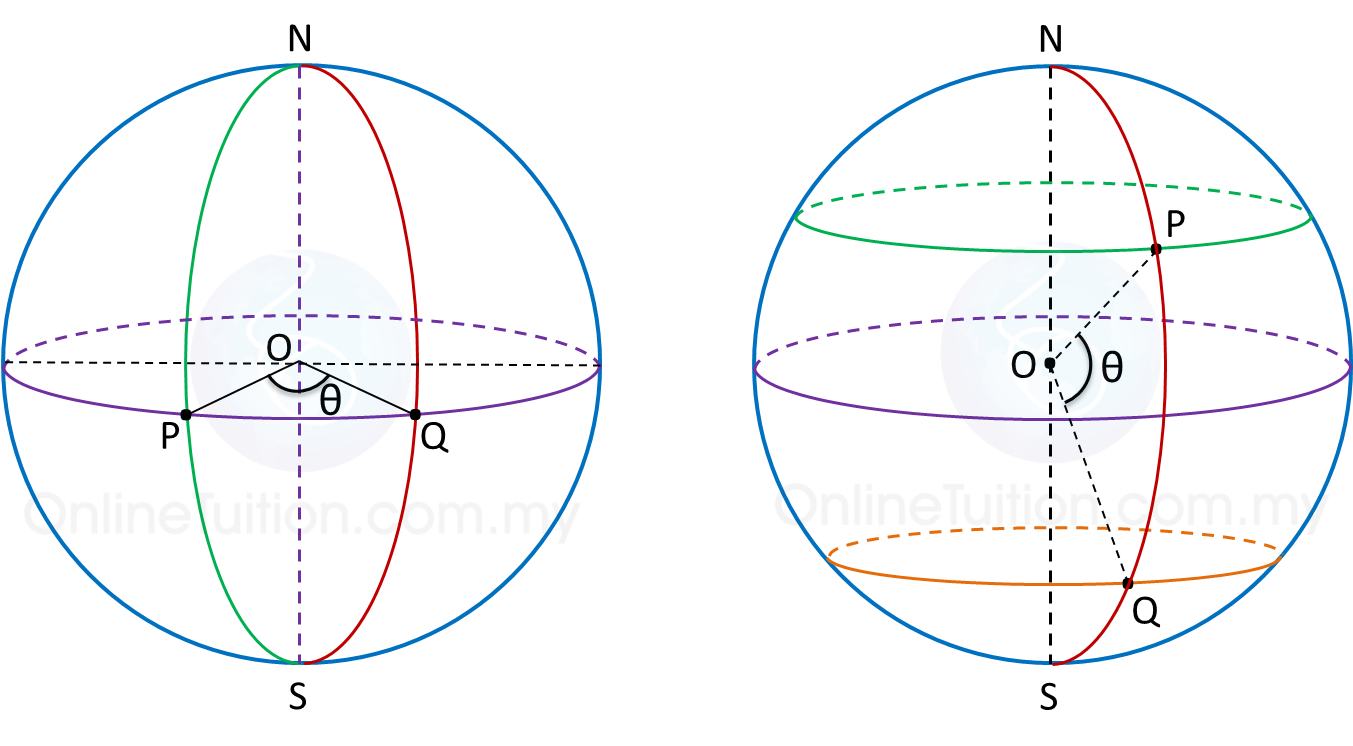
9.4.3 Shortest Distance between Two Points
 
1. The shortest distance between two points on the surface of the earth is the distance measured along a great circle.


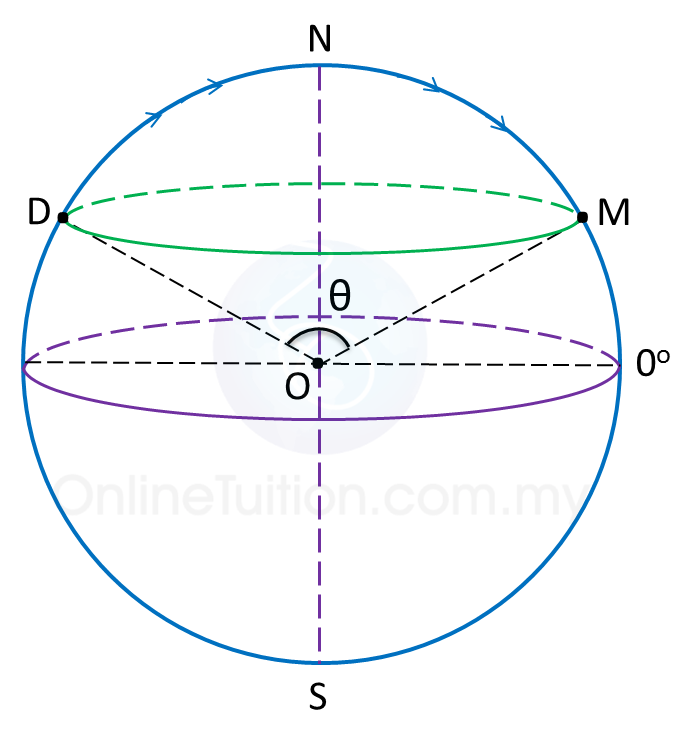
  Shortest distance between points D and M
   = ( θ × 60 ) nautical miles

Example:


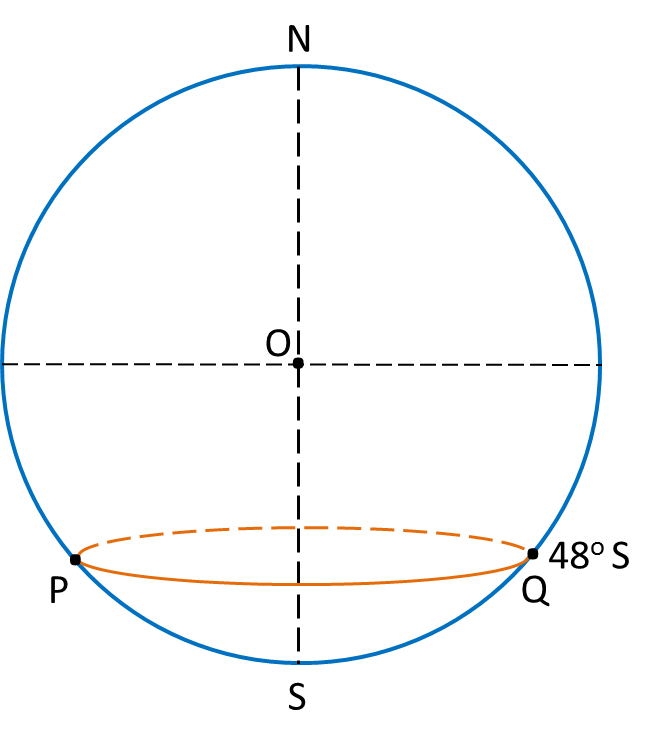
In the above diagram, calculate
(a) The distance from P to Q, measured along the parallel of latitude 48o S,
(b) The distance from P to Q, measured along the route PSQ, where S is the South Pole.
 State the shorter distance.

Solution:

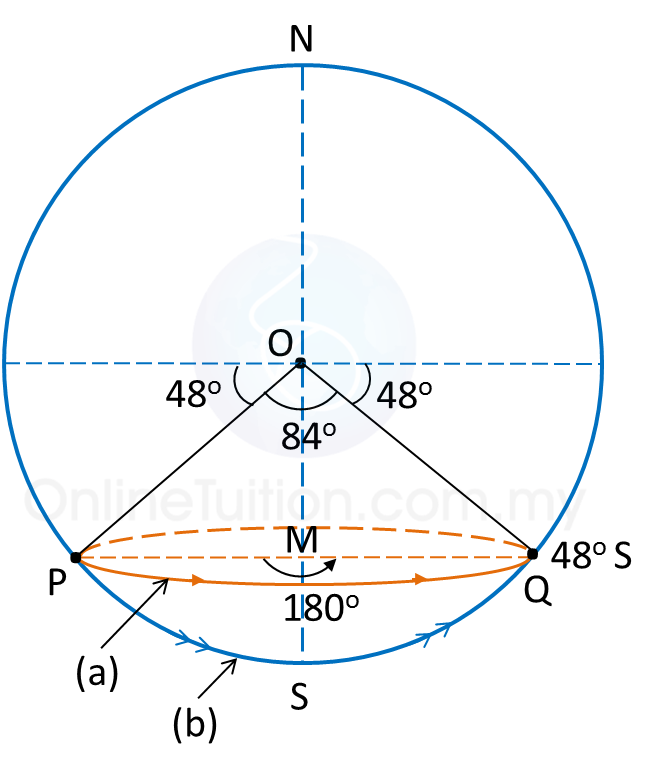
(a)
Distance from Pto Q, measured along the parallel of latitude 48o S
= 180 × 60 × cos 48o← (angle PMQ = 180o)
= 7266.61 n.m.
 
(b)
Distance from Pto Q, measured along the route PSQ, where S is the South Pole
= 84 × 60 ← (angle POQ = 180o – 48o – 48o = 84o)
= 5040 n.m.
 
The distance from P to Q, measured along the route PSQ in (b), where S is the South Pole, is shorter than the distance measured along the parallel of latitude in (a). 
 
  The shortest distance in the above example is    
  the distance along the arc of a great circle,   
  which passes through the South (or North) Pole.
 

9.1 Longitudes

Posted on by

9.1 Longitudes
 
1. A great circle is a circle with the centre of the Earth as its centre.
2. A meridian is half of a great circle from the North pole to the South pole.
3. The longitude of the Greenwich Meridian is 0o.
4. The longitude of a meridian is determined by:
   (a) The angle between the meridian plane and the Greenwich Meridian.
   (b) The position of the meridian to the east or west of the Greenwich Meridian.  

Example:

Longitude of P is 55o W.
Longitude of Q is 30o E.
 
5. All points on the same meridian have the same longitude.

Difference between Two Longitudes
1. If both the meridians are on the east (or west) of the Greenwich Meridian, subtract the angles of the longitudes.
2. If both the meridians are on the opposite sides of the Greenwich Meridian, add the angles of the longitudes.



9.2 Latitudes

Posted on by

9.2 Latitudes
 
1. The great circle which is perpendicular to the earth’s axis is called equator.

2. A latitude is the angle at the centre of the Earth which is subtended by the arc of a meridian starting from the Equator to the parallel of latitude.
 
3. A circle which is perpendicular to the Earth’s axis and parallel to the equator is called a parallel of latitude.
 
4. The latitude of the Equator is 0o.
 
5. All points on a parallel of latitude have the same latitude. 

Example:

Latitude of D is 30o N.
Latitude of E is 45o S.

Difference between Two Latitudes
1. If both parallels of latitude are on the north (or south) of the equator, subtract the angles of latitudes.
2. If both parallels of latitude are on the opposite sides of the equator, add the angles of the latitudes.

9.4 Distance on the Surface of the Earth

Posted on by

9.4 Distance on the Surface of the Earth

9.4.1 Distance between Two Points Along a Great Circle
 
1. A nautical mile is the length of an arc of a great circle that subtends an angle of one minute at the centre of the Earth.

2. The distance between two points on the surface of the earth is the arc of a circle that joins the two points.

3. To find the distance between two points along a meridian or the equator:



  Distance of P and Q
  = ( θ x 60 ) nautical miles


 



9.4.2 Distance between Two Points along a Parallel of Latitude

Posted on by

9.4.2 Distance between Two Points along a Parallel of Latitude
 
1. To find the distance along a parallel of latitude:

  Distance between points P and Q
  = ( different in longitude in minutes ) × cos latitude
  = ( θ × 60 × cos xo ) nautical miles

 
Example:

 
In the diagram above, calculate
(a) The distance of PQ, measured along the parallel of latitude 34o N,
(b) The distance of DM, measured along the parallel of latitude 54o S.
 
Solution:
(a)
Difference in longitude between P and Q
= 40o + 58o = 98o
Hence, the distance of PQ, measured along the parallel of latitude 34o N
= 98 × 60 × cos 34o← [θ × 60 × cos (latitude)]
= 4874.74 n.m.
 
(b)
Difference in longitude between D and M
= 82o – 40o = 42o
Hence, the distance of DM, measured along the parallel of latitude 54o S
= 42 × 60 × cos 54o← [θ × 60 × cos (latitude)]
= 1481.22 n.m.