Question 6:
The point M (x, 4), is the midpoint of the line joining straight line Q (-2, -3) and R (14, y).
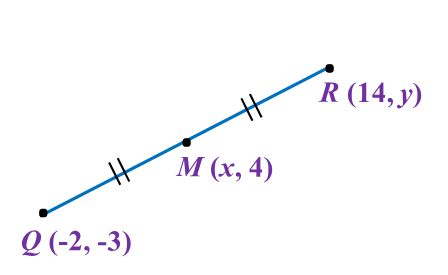 The value of x and y are
The value of x and y are
Solution:
x=−2+142x=122x=64=−3+y28=−3+yy=11
The point M (x, 4), is the midpoint of the line joining straight line Q (-2, -3) and R (14, y).
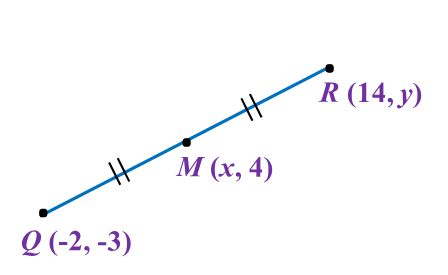 The value of x and y are
The value of x and y areSolution:
x=−2+142x=122x=64=−3+y28=−3+yy=11
Question 7:
In diagram below, PQR is a right-angled triangle. The sides QR and PQ are parallel to the y-axis and the x-axis respectively. The length of QR = 6 units.
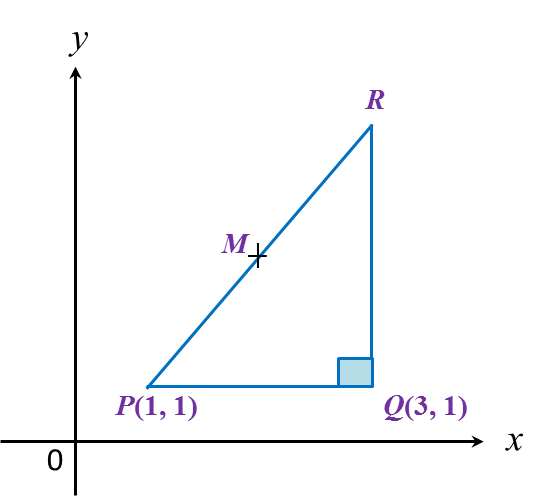
Given that M is the midpoint of PR, then the coordinates of M are
Solution:
x-coordinate of R = 3
y-coordinate of R = 1 + 6 = 7
R = (3, 7)
P(1,1),R(3,7)Coordinates of M=(1+32,1+72)=(2,4)
In diagram below, PQR is a right-angled triangle. The sides QR and PQ are parallel to the y-axis and the x-axis respectively. The length of QR = 6 units.

Given that M is the midpoint of PR, then the coordinates of M are
Solution:
x-coordinate of R = 3
y-coordinate of R = 1 + 6 = 7
R = (3, 7)
P(1,1),R(3,7)Coordinates of M=(1+32,1+72)=(2,4)
Question 8:
Given points P (–2, 8) and Q (10, 8), find the length of PQ.
Solution:
Length of PQ=√[10−(−2)]2+(8−8)2=√(14)2+0=14 units
Given points P (–2, 8) and Q (10, 8), find the length of PQ.
Solution:
Length of PQ=√[10−(−2)]2+(8−8)2=√(14)2+0=14 units
Question 9:
In diagram below, ABC is an isosceles triangle.
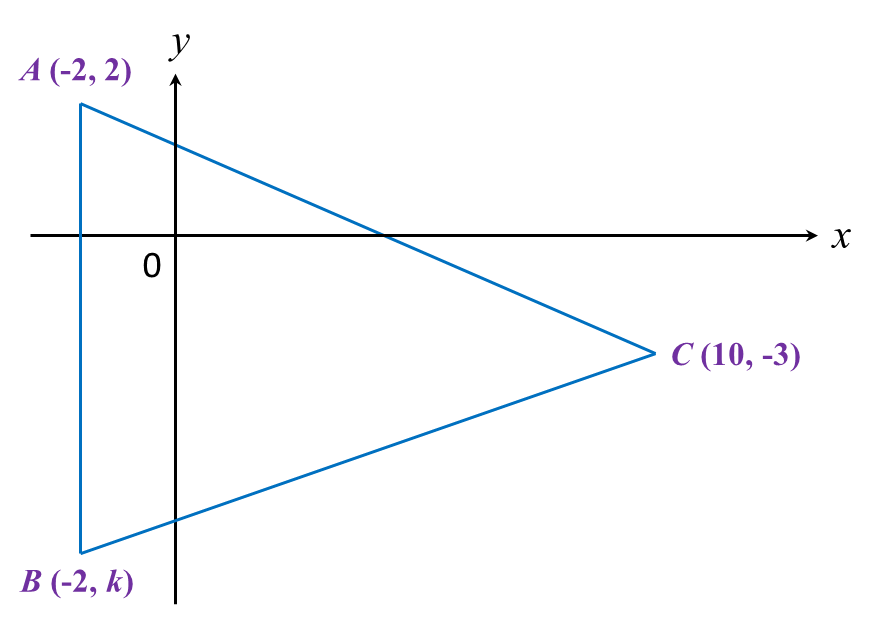
Find
(a) the value of k,
(b) the length of BC.
Solution:
(a)For an isosceles triangle, y−coordinate of C is the midpoint of straight line AB.2+k2=−32+k=−6 k=−8(b)B=(−2,−8)BC=√[10−(−2)]2+[−3−(−8)]2 =√122+52 =13 units
In diagram below, ABC is an isosceles triangle.

Find
(a) the value of k,
(b) the length of BC.
Solution:
(a)For an isosceles triangle, y−coordinate of C is the midpoint of straight line AB.2+k2=−32+k=−6 k=−8(b)B=(−2,−8)BC=√[10−(−2)]2+[−3−(−8)]2 =√122+52 =13 units
Question 10:
Diagram below shows a rhombus PQRS drawn on a Cartesian plane. PS is parallel to x-axis.
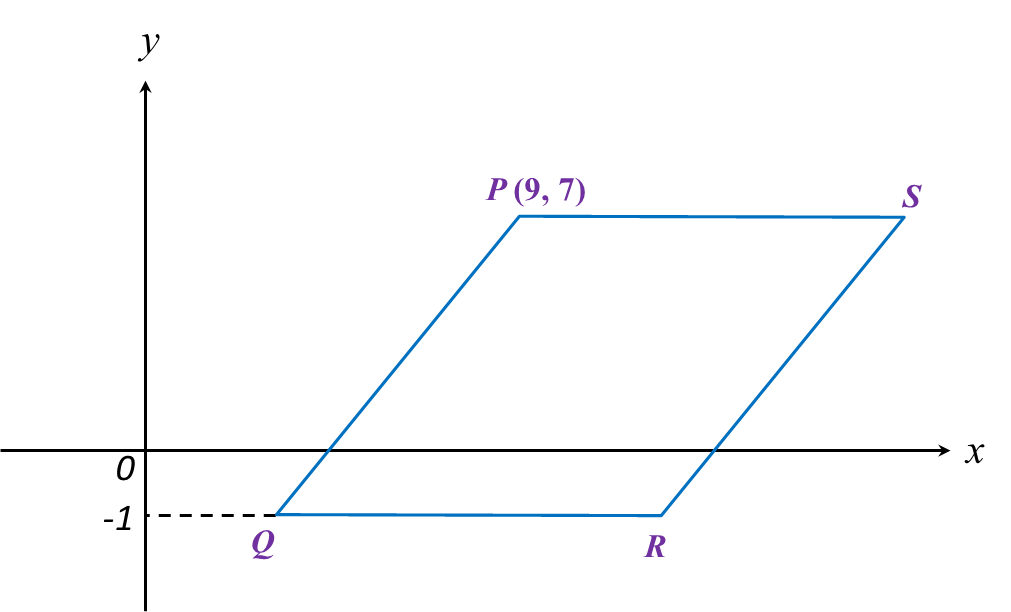
Given the perimeter of PQRS is 40 units, find the coordinates of point R.
Solution:
All sides of rhombus have the same length,therefore length of each side=404=10 unitsPQ=10(9−x1)2+(7−(−1))2=10281−18x1+x12+64=100x12−18x1+45=0(x1−3)(x1−15)=0x1=3,15x1=3Q=(3,−1),R=(x2,−1)QR=10(x2−3)2+[−1−(−1)]2=102x22−6x2+9+0=100x22−6x2−91=0(x2+7)(x2−13)=0x2=−7,13x2=13∴
Diagram below shows a rhombus PQRS drawn on a Cartesian plane. PS is parallel to x-axis.

Given the perimeter of PQRS is 40 units, find the coordinates of point R.
Solution:
All sides of rhombus have the same length,therefore length of each side=404=10 unitsPQ=10(9−x1)2+(7−(−1))2=10281−18x1+x12+64=100x12−18x1+45=0(x1−3)(x1−15)=0x1=3,15x1=3Q=(3,−1),R=(x2,−1)QR=10(x2−3)2+[−1−(−1)]2=102x22−6x2+9+0=100x22−6x2−91=0(x2+7)(x2−13)=0x2=−7,13x2=13∴
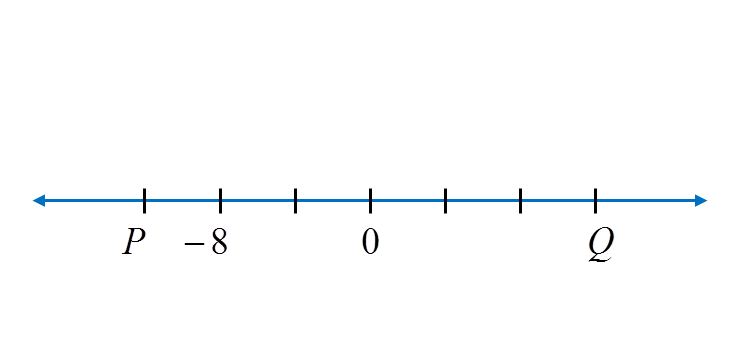 What is the value of P and of Q?
What is the value of P and of Q?