13.2.1 Statistics (I), PT3 Focus Practice

Posted on by

13.2.1 Statistics (I), PT3 Focus Practice
Question 1:
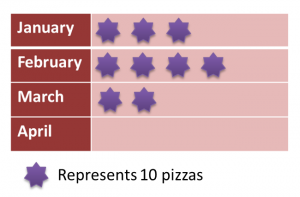
Diagram below is a pictograph showing the number of pizzas sold in three months.
 
The price of one pizza is RM18. The total sales for those four months are RM2250.
Calculate the number of pizzas sold in April.

Solution:
Total number of pizzas sold in four months
= R M 2250 R M 18 = 125

Total number of pizzas sold in first three months
= 9 × 10
= 90

Number of pizzas sold in April
= 125 – 90
= 35

Question 2:
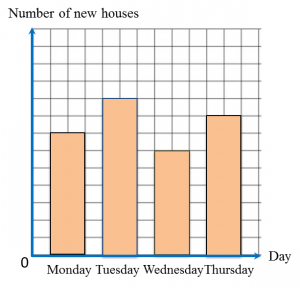
Diagram below is a bar chart showing the number of new houses sold over four days.
 

The total number of new houses sold on Wednesday and Thursday is 56.
Calculate the total number of new houses sold on Monday and Tuesday.

Solution:
Wednesday: 12 units
Thursday: 16 units
Number of houses represented by 1 unit
= 56 12+16 =2
Monday: 14 units
Tuesday: 18 units

Total number of new houses sold on Monday and Tuesday
= (14 + 8) × 2
= 64


Question 3:
Table below shows the number of companies that gave contributions to an orphan fund over a period of five days.

Days
Monday
Tuesday
Wednesday
Thursday
Friday
Number of companies
8
14
m
17
11

It is given that 20% of the total contribution was made on Tuesday.
Calculate the value of m. 

Solution:
Let C = Total contribution
20 100 × C = 14 C = 14 × 100 20 = 70 m = 70 − ( 8 + 14 + 17 + 11 ) = 70 − 50 = 20


4.7.4 The Oil Palm and Its Importance to National Development (Structured Questions)

Posted on by

Question 1:
Diagram 1.1 shows the process of latex coagulation.


(a)(i) State one example of chemical P? [1 mark]

(ii) State one characteristic of coagulated latex in Diagram 1.1. [1 mark]

(b) Chemical P in diagram 1.1 is replaced with chemical Q to prevent latex from coagulating.
State one example of chemical Q. [1 mark]


(c) Diagram 1.2 shows the process when natural rubber is heated with Sulphur to form rubber R.

  (i) Name process X. [1 mark]
  (ii) Name rubber R. [1 mark]

(d) Mark (\/) the object which is made of rubber R. [1 mark]




Answer:
(a)(i) Methanoic acid

(a)(ii) Elastic

(b) Ammonia solution

(c)(i) Vulcanization of rubber

(c)(ii) Vulcanized rubber

(d)



4.7.2 Alcohol and Its Effects on Health (Structured Questions)

Posted on by

Question 1:
Diagram 1.1 and Diagram 1.2 show an experiment to investigate the effect of temperature on the fermentation of glucose by yeast.



(a) State one hypothesis that can be made from this experiment. [1 mark]

(b) State the variables in this experiment.
  (i) Manipulated variable [1 mark]
  (ii) Responding variable [1 mark]

(c) Based on Diagram 1.1 and 1.2, which temperature is more suitable for the fermentation of glucose? [1 mark]


(d) Diagram 1.3 shows the graph of the volume of carbon dioxide produced at 35oC against time.

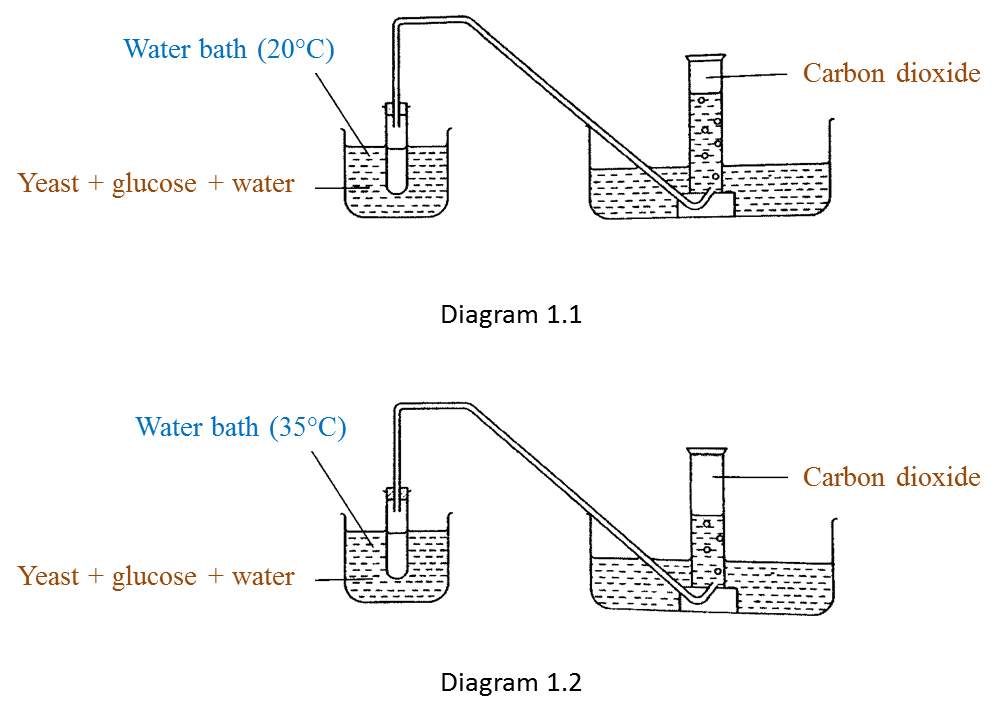
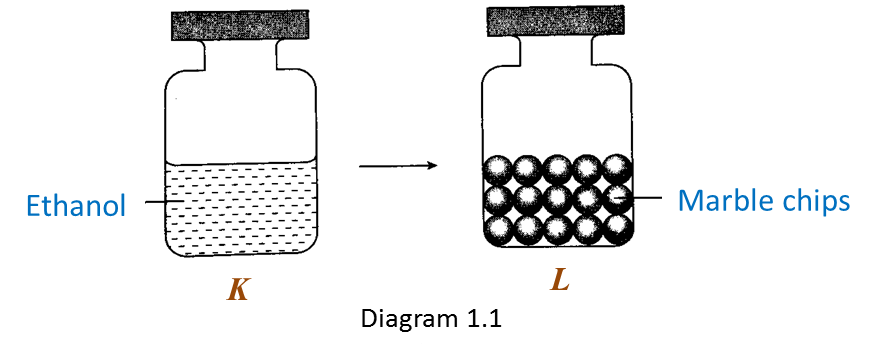
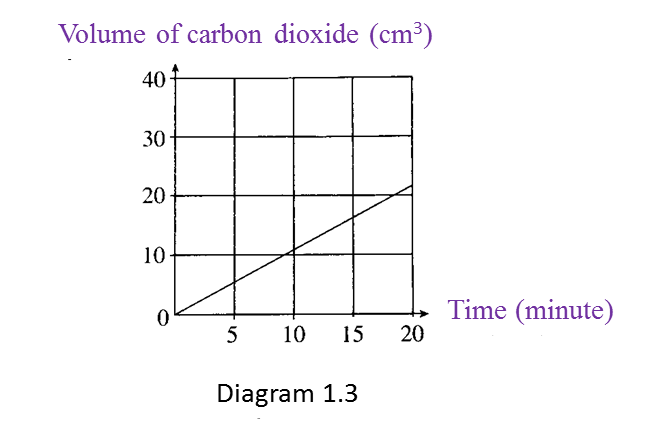What is the relationship between the volume of carbon dioxide produced and time? [1 mark]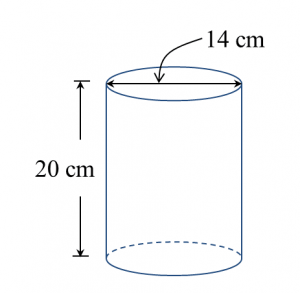


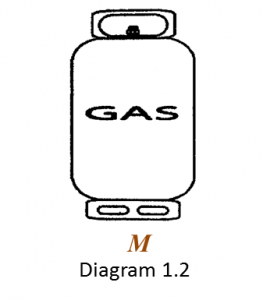Answer:
(a) Fermentation of glucose by yeast is affected by temperature.

(b)(i) Temperature of the water bath

(b)(ii) Volume of carbon dioxide produced

(c) 35oC

(d) The volume of carbon dioxide produced is directly proportional to time. 


12.2.1 Solid Geometry (II), PT3 Focus Practice

Posted on by

12.2.1 Solid Geometry (II), PT3 Focus Practice

Question 1:
Diagram below shows closed right cylinder.

Calculate the total surface area, in cm2, of the cylinder.  
( π = 22 7 )

Solution:
Total surface area
= 2(πr2) + 2πrh
= ( 2 × 22 7 × 7 2 ) + ( 2 × 22 7 × 7 × 20 ) = 308 + 880 = 1188 c m 2



Question 2:
Diagram below shows a right prism with right-angled triangle ABC as its uniform cross section.
Calculate the total surface area, in cm2, of the prism.

Solution:
A B = 5 2 − 3 2 = 25 − 9 = 16 = 4 c m

Total surface area
= 2 (½× 3 × 4) + (3 × 10) + (4 × 10) + (5 × 10)
= 12 + 30 + 40 + 50
= 132 cm2


Question 3:
Diagram below shows a right pyramid with a square base.

Calculate the total surface area, in cm2, of the right pyramid.  

Solution:
h2= 102 – 62
   = 100 – 36
   = 64
h = √64
   = 8cm

Total surface area of the right pyramid
= (12 × 12) + 4 × (½× 12 × 8)
= 144 + 192
= 336 cm2


Question 4:

The diagram shows a cone. The radius of its base is 3.5 cm and its slant height is 6 cm. Find the area of its curved surface.
( π= 22 7 )

Solution:
Area of curved surface
= π × radius of base × slant height
= πrs
= 22 7 × 3.5 × 6 = 66 c m 2


4.7.1 Various Carbon Compound (Structured Questions)

Posted on by

Question 1:
Diagram 1.1 shows two examples of carbon compounds, K and L.



(a)(i) Based on Diagram 1.1, which one is an inorganic carbon compound? [1 mark]

(ii) State one characteristic of an inorganic carbon compound. [1 mark]

(b)(i) State one use of compound K. [1 mark]

(ii) State one effect of compound K on the nervous system if consumed excessively. [1 mark]

(c) Diagram 1.2 shows a tank containing gas M used for gas stoves.
Gas M is a hydrocarbon compound.

(i) State two elements present in gas M. [1 mark]
 
(ii) State one source of gas M. [1 mark]


Answer:
(a)(i) L or marble chips

(a)(ii) Originates from non-living things or does not originates from living things

(b)(i) Alcoholic drink

(b)(ii) Disrupts nerve coordination or slows down the transmission of impulses

(c)(i)
1. Hydrogen
2. Carbon

(c)(ii) Petroleum


11.2.2 Transformations (I), PT3 Focus Practice

Posted on by

Question 6:
Diagram in the answer space shows a Cartesian plane board used in an indoor game.
The instruction of the game is such that the first move follows the translation ( −4 −2 ) and the second move follows the translation (   5 −4 ) .
Jimmy starts moving from the position mark x.
(a) Mark T1 at Jimmy’s position after the first move and T2 at the position after the second move.
(b) State the coordinates of the position based on Jimmy’s final move.

Answer:


Solution:
(a)




(b) Jimmy’s final position = (3, –2).


Question 7:
In the answer space below, a quadrilateral PQRS is drawn on a grid of squares. A’ is the image of P under rotation 90o at point C.
(a) State the direction of the rotation.
In the answer space,
(b) mark B’ as the image of point Q under the same rotation.
(c) draw the image of quadrilateral PQRS under a reflection on the line MN.

Answer:


Solution:
(a) A’ is the image of P under a rotation of 90o clockwise about the centre C.

(b) and (c)




Question 8:
Diagram in the answer space shows trapezium ABCD drawn on a Cartesian plane. A’D’ is the image of AD under a rotation at centre W.
(a) State
(i) angle of rotation
(ii) the direction of the rotation.
(b) On diagram in the answer space, complete the image of trapezium ABCD.

Answer:



Solution:
(a)(i)
∠DWD'= 90 o  or  270 o .

(a)(ii) Anticlockwise or clockwise.

(b)



11.2.1 Transformations (I), PT3 Focus Practice

Posted on by

11.2.1 Transformations (I), PT3 Focus Practice

Question 1:
Diagram below in the answer space shows object P drawn on a grid of equal squares with sides of 1 unit.
On the diagram, draw the image of object P under the translation ( − 6 3 ) .   

Answer:

Solution:

Question 2:
Describe the translation which maps point P onto point P’.


Solution:

The translation is ( 7 − 6 ) .  


Question 3:
Diagram below in the answer space shows quadrilateral PQRS. R’S’ is the image of RS under a reflection in the straight line AB.
On diagram in the answer space, complete the image of quadrilateral PQRS.

Answer:

 
Solution:
 

Question 4:
Diagram in the answer space, shows two polygons, M and M’, drawn on a grid of equal squares with sides of 1 unit. M’ is the image of M under a reflection.
(a) Draw the axis of reflection.
(b) Mark the image of P under the same reflection.
(c) Draw the image of M under reflection in the x-axis.

Answer:
 
Solution:



Question 5:
On diagram in the answer space, triangle P’Q’R’ is the image of triangle PQR under a rotation about centre C.
(a) State the angle and direction of the rotation.
(b) K’is the image of point K under the same rotation.
Mark and state the coordinates of K’.

Answer:


Solution:

(a) ∆ P’Q’R’ is the image of ∆ PQR under a clockwise rotation of 90o.
(b) Image of K = (1, –4).


11.1 Transformations (I)

Posted on by

11.1 Transformations (I)

11.1.1 Transformation
A transformation is a one-to-one correspondence or mapping between points of an object and its image on a plane. 


11.1.2 Translation
1. A translation is a transformation which moves all the points on a plane through the same distance in the same direction.
 
2. Under a translation, the shape, size and orientation of object and its image are the same.
 
3. A translation in a Cartesian plane can be represented in the form ( a b ) ,  whereby, a represents the movement to the right or left which is parallel to the x-axis and b represents the movement upwards or downwards which is parallel to the y-axis.

Example 1:
Write the coordinates of the image of A (–2, 4) under a translation ( 4 − 3 )  and B (1, –2) under a translation ( − 5 3 ) .

Solution:
 
A’ = [–2 + 4, 4 + (–3)] = (2, 1)
B’ = [1 + (–5), –2 + 3] = (–4, 1)

Example 2:
Point K moved to point K’ (3, 8) under a translation ( − 4 3 ) .  
What are the coordinates of point K?

Solution:
K ( x , y ) → ( − 4 3 ) → K ' ( 3 , 8 )
The coordinates of K = [3 – (– 4), 8 – 3]
= (7, 5)

Therefore the coordinates of K are (7, 5).



11.1.3 Reflection
1. A reflection is a transformation which reflects all points of a plane in a line called the axis of reflection.
2. In a reflection, there is no change in shape and size but the orientation is changed. Any points on the axis of reflection do not change their positions.

Example 3:

11.1.4 Rotation
1. A rotation is a transformation which rotates all points on a plane about a fixed point known as the centre of rotation through a given angle in a clockwise or anticlockwise direction.
2. In a rotation, the shape, size and orientation remain unchanged.
3. The centre of rotation is the only point that does not change its position.

Example 4:
Point A (3, –2) is rotated through 90o clockwise to A’ and 180o anticlockwise to A1 respectively about origin.
State the coordinates of the image of point A.

Solution:
Image A’ = (–2, 3)
Image A1 = (–3, 2) 


11.1.5 Isometry
1. An isometry is a transformation that preserves the shape and size of an object.
2.Translation, reflection and rotation and a combination of it are isometries.


11.1.6 Congruence
1. Congruent figures have the same size and shape regardless of their orientation.
2. The object and the image obtained under an isometry are congruent.

10.2.3 Circles I, PT3 Focus Practice

Posted on by

Question 11:
The Town Council plans to build an equilateral triangle platform in the middle of a roundabout. The diameter of circle RST is 24 m and the perpendicular distance from R to the line ST is 18 m. as shown in Diagram below.
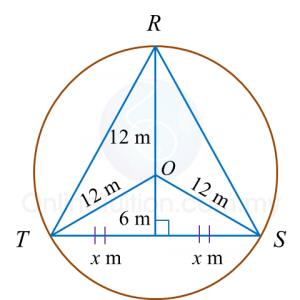
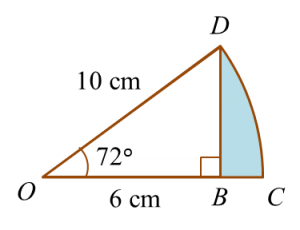
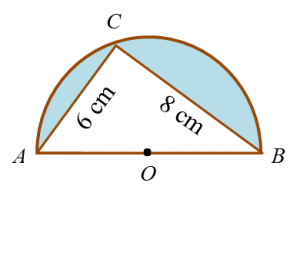
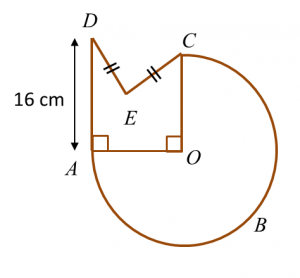
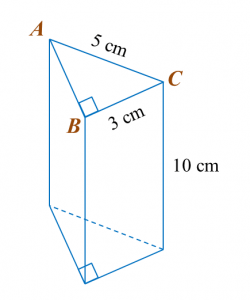
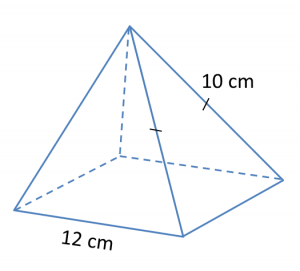
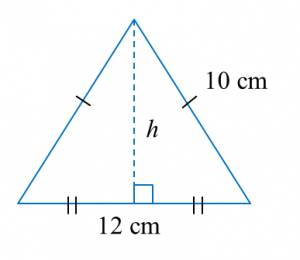
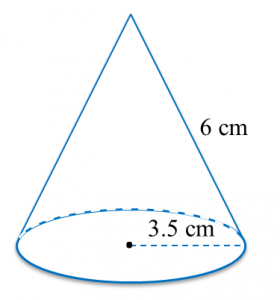
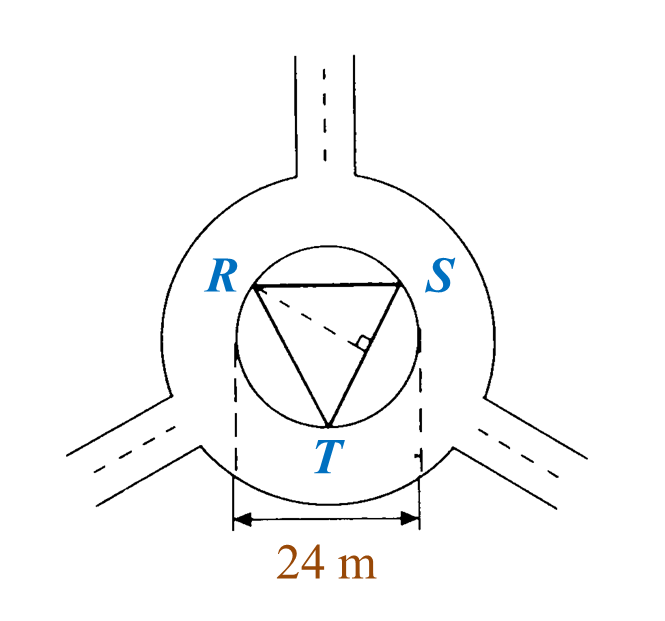Find the perimeter of the platform.

Solution:

Given diameter = 24 m
hence radius = 12 m
O is the centre of the circle.
Using Pythagoras’ theorem:
x 2 = 12 2 − 6 2 x= 144−36   =10.39 m TS=RS=RT  =10.39 m ×2  =20.78 m Perimeter of the platform TS+RS+RT =20.78×3 =63.34 m

Question 12:
Amy will place a ball on top of a pillar in Diagram below. Table below shows the diameters of three balls X, Y and Z.


Which ball X, Y or Z, can fit perfectly on the top of the pillar? Show the calculation to support Amy’s choice.

Solution:

Let the radius of the top of the pillar=r cm. O is the centre of the circle. In Δ OQR, r 2 = ( r−4 ) 2 + 8 2  ( using Pythagoras' theorem ) r 2 = r 2 −8r+16+64 r 2 = r 2 −8r+80 r 2 − r 2 +8r=80 8r=80 r= 80 8 r=10 cm Therefore, diameter =2×10 =20 cm Ball Y with diameter 20 cm can fit perfectly  on top of the pillar.

Question 13:
Diagram below shows a rim of a bicycle wheel with a diameter of 26 cm. Kenny intends to build a holder for the rim.

Which of the rim holder, X, Y or Z, can fit the bicycle rim perfectly? Show the calculation to support your answer.

Solution:

Let the radius of the rim holder=r cm. O is the centre of the circle. In Δ OQR, r 2 = ( r−8 ) 2 + 12 2  ( using Pythagoras' theorem ) r 2 = r 2 −16r+64+144 r 2 = r 2 −16r+208 r 2 − r 2 +16r=208 16r=208 r= 208 16 r=13 cm Therefore, diameter =2×13 =26 cm Rim holder Z with diameter 26 cm can fit the bicycle perfectly.


10.2.2 Circles I, PT3 Focus Practice

Posted on by

Question 6:
In the diagram below, CD is an arc of a circle with centre O.


Determine the area of the shaded region.
( Use π= 22 7 )

Solution:
Area of sector=Area of circle× 72 o 360 o                       = 22 7 × ( 10 ) 2 × 72 o 360 o                       = 440 7  cm 2 Area of ΔOBD= 1 2 ×6×8                        =24  cm 2 Area of shaded region= 440 7 −24                                   =38 6 7  cm 2


Question 7:
In diagram below, ABC is a semicircle with centre O.

Calculate the area, in cm2 , of the shaded region.
( Use π= 22 7 )

Solution:
∠ACB= 90 o AB= 6 2 + 8 2     = 100     =10 cm Radius=10÷2            =5 cm The shaded region =( 1 2 × 22 7 ×5×5 )−( 1 2 ×6×8 ) =39 2 7 −24 =15 2 7  cm 2

Question 8:
In diagram below, ABC is an arc of a circle centre O

The radius of the circle is 14 cm and AD = 2 DE.
Calculate the perimeter, in cm, of the whole diagram.
( Use π= 22 7 )

Solution:
Length of arc ABC = 3 4 ×2πr = 3 4 ×2× 22 7 ×14 =66 cm Perimeter of the whole diagram =16+8+8+66 =98 cm

[adinserter block="3"]
Question 9:
In diagram below, KLMN is a square and KLON is a quadrant of a circle with centre K.



Calculate the area, in cm2, of the coloured region.
( Use π= 22 7 )

Solution:
Area of the coloured region = 45 o 360 o ×π r 2 = 45 o 360 o × 22 7 × 14 2 =77  cm 2


[adinserter block="3"]
Question 10:
Diagram below shows two quadrants, AOC and EOD with centre O.



Sector AOB and sector BOC have the same area.
Calculate the area, in cm2, of the coloured region.
( Use π= 22 7 )

Solution:
Area of the sector AOB=Area of the sector BOC Therefore, ∠AOB=∠BOC                             = 90 o ÷2                             = 45 o Area of the coloured region = 45 o 360 o × 22 7 × 16 2 =100 4 7  cm 2