7.2.1 Geometrical Constructions, PT3 Focus Practice
Question 1:
Diagram below in the answer space shows part of triangle ABC.
(a) Using a pair of compasses, a protractor and a ruler, draw a triangle ABC starting from the line given in the answer space with AB = 4.5 cm, BC = 6 cm and ∠ABC = 105o.
(b) Measure ∠BCA.
Answer:
(a)

Solution:
(a)


(b)
∠BCA = 31o
Question 2:
Diagram below shows a triangle ABC drawn not to scale.
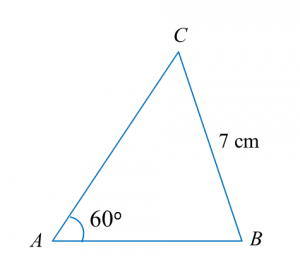

Diagram in the answer space shows a straight line AB.
(a) Using only a ruler and a pair of compasses, construct
(i) triangle ABC to the measurements shown in diagram above,
(ii) the perpendicular line to the straight line AC which passes through the point B.
(b) Measure the perpendicular distance between straight line AC and point B.
Answer:
(a)(i),(ii)

Solution:
(a)(i),(ii)
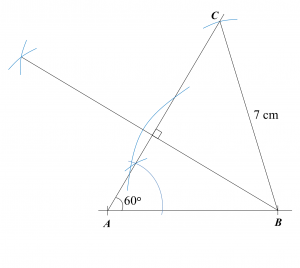
(b)
5.3 cm
Question 3:
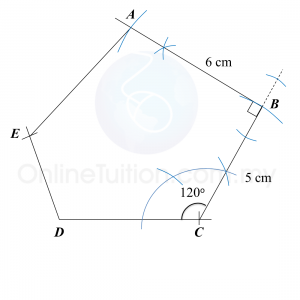
Diagram below shows a pentagon ABCDE.


Using only a ruler and a pair of compasses, construct the diagram, beginning from the straight lines CD and DE provided in the answer space.
Answer:
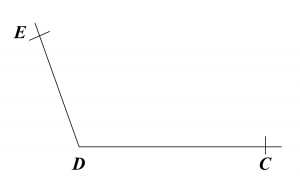
Solution:

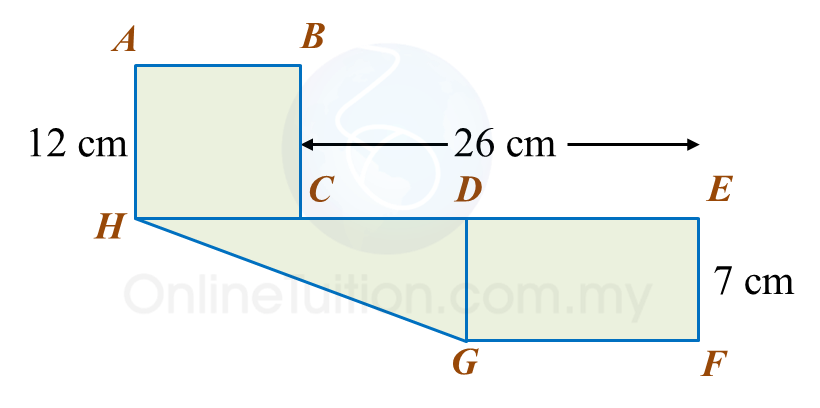

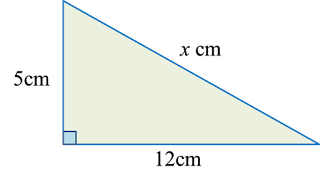
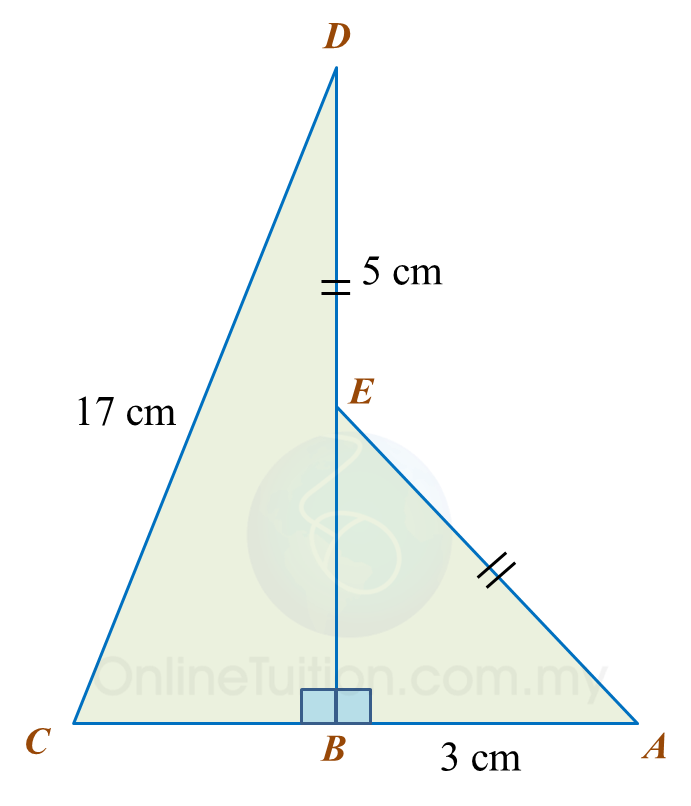 Find the length, in cm, of BC. Round off the answer to two decimal places.
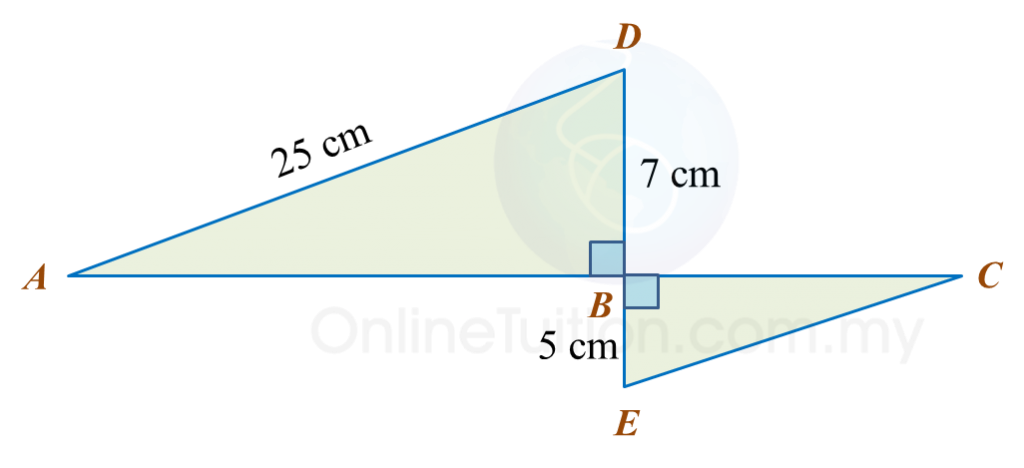
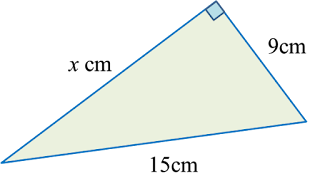
Find the length, in cm, of BC. Round off the answer to two decimal places.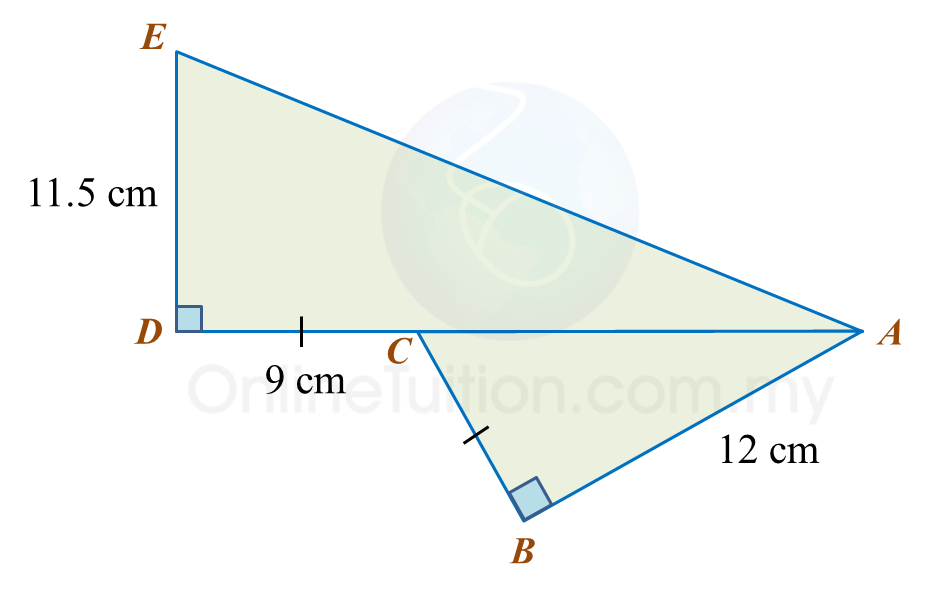 Find the length, in cm, of AE. Round off the answer to one decimal places.
Find the length, in cm, of AE. Round off the answer to one decimal places.



 (a) State the ratio of the number of chicken eggs to the number of duck eggs.
(a) State the ratio of the number of chicken eggs to the number of duck eggs.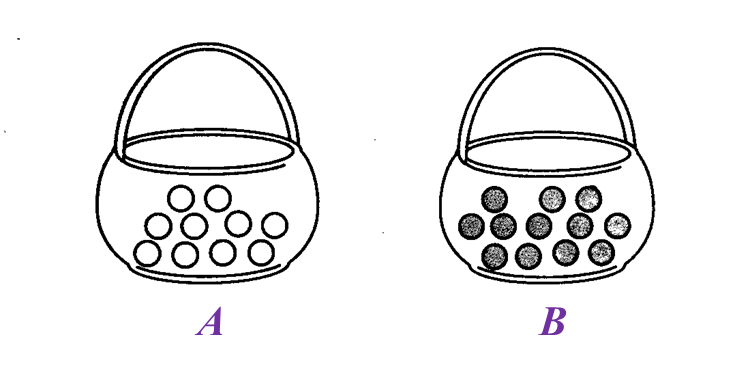 (a) State the ratio of the number of candies in basket A to the number of candies in basket B.
(a) State the ratio of the number of candies in basket A to the number of candies in basket B.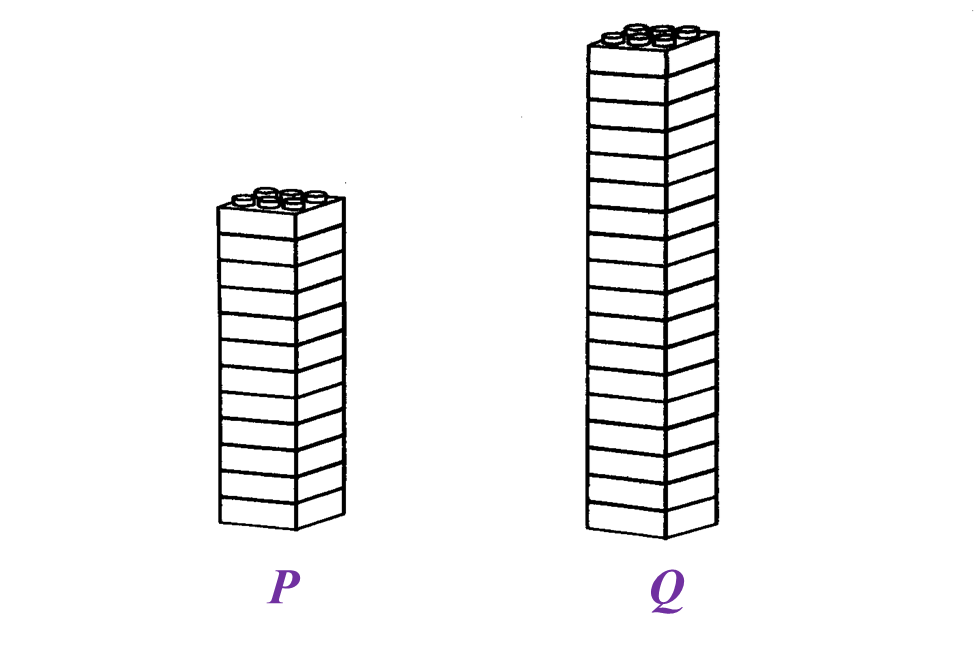 (a) State the ratio of the number of toy bricks in Tower P to the number of toy bricks in Tower Q.
(a) State the ratio of the number of toy bricks in Tower P to the number of toy bricks in Tower Q.
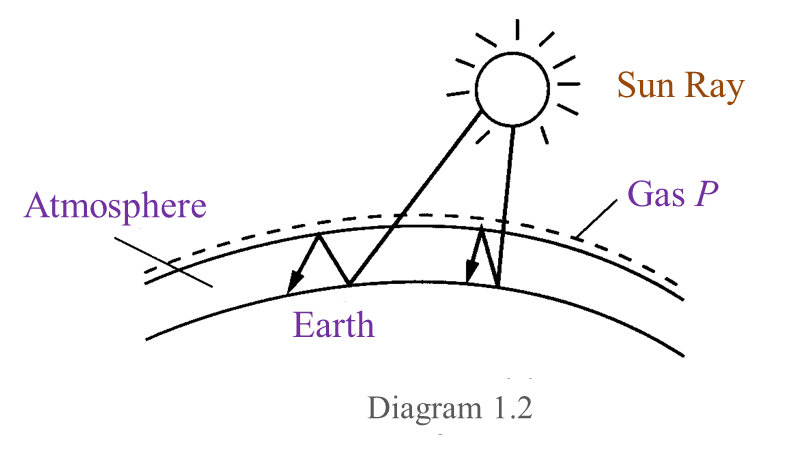 (i) Name gas P. [1 mark]
(i) Name gas P. [1 mark]