10.2.1 Transformations II, PT3 Focus Practice

10.2.1 Transformations II, PT3 Focus Practice

Question 1:

In the diagram, ∆P’Q’R’ is the image of ∆PQR under an enlargement.

(a) State the scale factor of the enlargement.

(b) If the area of ∆PQR = 7 cm², calculate the area of ∆P’Q’R’.

Solution:

(a)

Scale factor, k = \frac{P' Q'}{P Q} = \frac{6}{3} = 2

(b)

Area of image = k²× Area of object

Area of ∆P’Q’R’ = 2²× 7

= 28 cm²

Question 2:

In diagram below, OP’Q’ is the image of OPQ under an enlargement with centre O.

Given PQ = 4cm, calculate the length, in cm, of P’Q’.

Solution:

\begin{array}{l} \frac{P' Q'}{P Q} = \frac{O P'}{O P} \\ \frac{P' Q'}{4} = \frac{9}{3} \\ P' Q' = \frac{9}{3} \times 4 \\ = 12 cm \end{array}

Question 3:

In diagram below, PQ’R’S’ is the image of PQRS under an enlargement.

Calculate the length, in cm, of SS’.

Solution:

\begin{array}{l} \frac{P S}{P S'} = \frac{P Q}{P Q'} \\ \frac{P S}{36} = \frac{4}{16} \\ P S = \frac{4}{16} \times 36 \\ = 9 cm \\ S S' = 36 - 9 \\ = 27 cm \end{array}

Question 4:

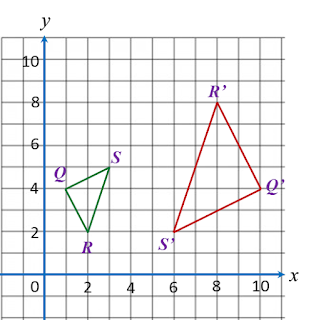
On the Cartesian plane, Q’R’S’ is the image of ∆ QRS under an enlargement of centre T.

State the coordinates of T.

Solution:

Coordinates of T = (4, 4).

Question 5:

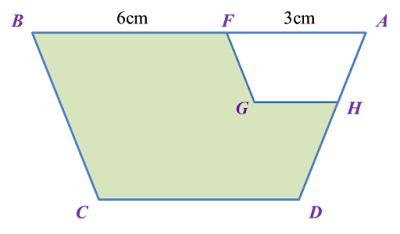
In diagram below, quadrilateral AFGH is the image of ABCD under an enlargement.

(a) Find the scale factor of the enlargement.

(b) The area represented by the quadrilateral AFGH is 15cm². Find the area, in cm², represented by the shaded region.

Solution:

(a)

\begin{array}{l} Scale factor \\ = \frac{3}{6 + 3} = \frac{3}{9} = \frac{1}{3} \end{array}

(b)

Area of image = k²× Area of object

\begin{array}{l} 15 = {(\frac{1}{3})}^{2} \times Area of object \\ Area of object = 15 \times 9 = 135 \\ Area of shaded region = 135 - 15 \\ = 120 c m^{2} \end{array}