Soalan 8 (3 markah):
Rajah menunjukkan graf garis lurus
 Rajah
Rajah
Berdasarkan Rajah, ungkapkan y dalam sebutan x.
Penyelesaian:
Rajah menunjukkan graf garis lurus
 Rajah
RajahBerdasarkan Rajah, ungkapkan y dalam sebutan x.
Penyelesaian:
Soalan 9 (3 markah):
Pembolehubah x dan y dihubungkan oleh persamaan , dengan keadaan r ialah pemalar. Rajah menunjukkan graf garis lurus yang diperoleh dengan memplotkan
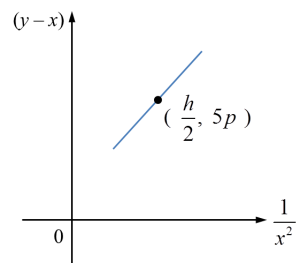 Rajah
Rajah
Ungkapkan h dalam sebutan p dan r.
Penyelesaian:
Pembolehubah x dan y dihubungkan oleh persamaan , dengan keadaan r ialah pemalar. Rajah menunjukkan graf garis lurus yang diperoleh dengan memplotkan
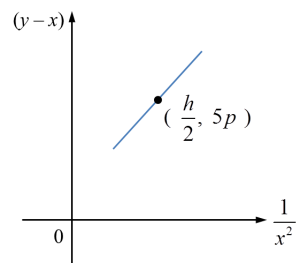 Rajah
RajahUngkapkan h dalam sebutan p dan r.
Penyelesaian: