5.2.3 Indices, PT3 Practice

Posted on February 9, 2018 by user

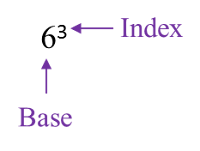
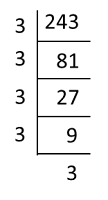
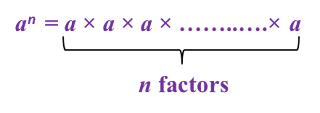Question 13:

$Solve: 3^{2 n + 1} = \frac{3^{n} \times 9}{{(9^{\frac{1}{2}})}^{- 3}}$

Solution:

$\begin{array}{l} 3^{2 n + 1} = \frac{3^{n} \times 9}{{(9^{\frac{1}{2}})}^{- 3}} \\ 3^{2 n + 1} = \frac{3^{n} \times 3^{2}}{3^{- 3}} \\ 3^{2 n + 1} = 3^{n + 2 - (- 3)} \\ 2 n + 1 = n + 5 \\ n = 4 \end{array}$

Question 14:

$Given that k^{3} = 9^{- \frac{3}{2}} \times 64^{\frac{1}{2}}, find the value of k .$

Solution:

$\begin{array}{l} k^{3} = 9^{- \frac{3}{2}} \times 64^{\frac{1}{2}} \\ = {(3^{2})}^{- \frac{3}{2}} \times {(2^{6})}^{\frac{1}{2}} \\ = 3^{- 3} \times 2^{3} \\ = {(\frac{2}{3})}^{3} \\ k = \frac{2}{3} \end{array}$

Question 15:

${Given 9}^{x + 2} \div 3^{4} = 3^{x + 1}, calculate the value of x .$

Solution:

$\begin{array}{l} 9^{x + 2} \div 3^{4} = 3^{x + 1} \\ {(3^{2})}^{x + 2} \div 3^{4} = 3^{x + 1} \\ 3^{2 x + 4} \div 3^{4} = 3^{x + 1} \\ 2 x + 4 - 4 = x + 1 \\ 2 x = x + 1 \\ x = 1 \end{array}$

Question 16:

$Simplify: {(\frac{- 2 x^{5} y^{- 2}}{z^{\frac{1}{6}}})}^{3} \div \frac{1}{\sqrt{x^{2} z}}$

Solution:

$\begin{array}{l} {(\frac{- 2 x^{5} y^{- 2}}{z^{\frac{1}{6}}})}^{3} \div \frac{1}{\sqrt{x^{2} z}} \\ = \frac{- 8 x^{15} y^{- 6}}{z^{\frac{1}{2}}} \times \sqrt{x^{2} z} \\ = \frac{- 8 x^{15} y^{- 6}}{z^{\frac{1}{2}}} \times {(x^{2} z)}^{\frac{1}{2}} \\ = \frac{- 8 x^{15} y^{- 6}}{z^{\frac{1}{2}}} \times x z^{\frac{1}{2}} \\ = - 8 x^{15 + 1} y^{- 6} \\ = \frac{- 8 x^{16}}{y^{6}} \end{array}$

Question 17:

Find the value of the following.

(a) (2³)²× 2⁴÷ 2⁵

(b)

$\frac{a^{2} \times a^{\frac{1}{2}}}{{(a^{\frac{2}{3}} \times a^{\frac{1}{3}})}^{- 2}}$

Solution:

(a)

(2³)²× 2⁴÷ 2⁵= 2⁶× 2⁴÷ 2⁵

= 2^6+4-5

= 2⁵

= 32

(b)

$\begin{array}{l} \frac{a^{2} \times a^{\frac{1}{2}}}{{(a^{\frac{2}{3}} \times a^{\frac{1}{3}})}^{- 2}} = \frac{a^{2 + \frac{1}{2}}}{{(a^{\frac{2}{3}} \times a^{\frac{1}{3}})}^{- 2}} \\ = \frac{a^{2 + \frac{1}{2}}}{{(a^{\frac{2}{3} + \frac{1}{3}})}^{- 2}} \\ = \frac{a^{\frac{5}{2}}}{a^{- 2}} \\ = a^{\frac{5}{2} - (- 2)} \\ = a^{\frac{5}{2} + \frac{4}{2}} \\ = a^{\frac{9}{2}} \end{array}$

5.2.2 Indices, PT3 Practice

Posted on February 7, 2018 by user

Question 7:
Given that

$2^{8 - x} =32$ , calculate the value of x.

Solution:

$\begin{array}{l} 2^{8 - x} =32 \\ 2^{8 - x} {=2}^{5} \\ 8 - x = 5 \\ - x = - 3 \\ x = 3 \end{array}$

Question 8:

$Given 3^{2 p - 1} = (3^{p}) (3^{2}), calculate the value of p .$

Solution:

$\begin{array}{l} 3^{2 p - 1} = (3^{p}) (3^{2}) \\ 3^{2 p - 1} = 3^{p + 2} \\ 2 p - 1 = p + 2 \\ p = 3 \end{array}$

Question 9:

$Given that 8 \times 8^{p + 1} = (8^{5}) (8^{3}), find the value of p .$

Solution:

$\begin{array}{l} 8 \times 8^{p + 1} = (8^{5}) (8^{3}) \\ 8^{1 + p + 1} = 8^{5 + 3} \\ 2 + p = 8 \\ p = 6 \end{array}$

Question 10:

$Given that \frac{2^{5} \times 2^{7}}{2^{10}} = 2^{p}, find the value of p .$

Solution:

$\begin{array}{l} \frac{2^{5} \times 2^{7}}{2^{10}} = 2^{p} \\ 2^{5 + 7 - 10} = 2^{p} \\ 2^{2} = 2^{p} \\ p = 2 \end{array}$

Question 11:

$Simplify: \frac{12 p^{10} q^{6}}{3 p^{4} q^{2} \times {(4 p q^{3})}^{2}}$

Solution:

$\begin{array}{l} \frac{12 p^{10} q^{6}}{3 p^{4} q^{2} \times {(4 p q^{3})}^{2}} = \frac{12 p^{10} q^{6}}{3 p^{4} q^{2} \times 16 p^{2} q^{6}} \\ = \frac{12^{1} p^{10 - 4 - 2} q^{6 - 2 - 6}}{3^{1} \times 16^{4}} \\ = \frac{p^{4} q^{- 2}}{4} \\ = \frac{p^{4}}{4 q^{2}} \end{array}$

Question 12:

$Simplify: \frac{a b^{2} \times {(8 a^{3} b^{6})}^{\frac{1}{3}}}{{(a^{2} b^{4})}^{\frac{1}{2}}}$

Solution:

$\begin{array}{l} \frac{a b^{2} \times {(8 a^{3} b^{6})}^{\frac{1}{3}}}{{(a^{2} b^{4})}^{\frac{1}{2}}} = \frac{a b^{2} \times (8^{^{\frac{1}{3}}} a^{3}^{(\frac{1}{3})} b^{6 (\frac{1}{3})})}{a^{2 (\frac{1}{2})} b^{4 (\frac{1}{2})}} \\ = \frac{a b^{2} \times 2 a b^{2}}{a b^{2}} \\ = 2 a b^{2} \end{array}$

5.2.1 Indices, PT3 Practice

Posted on February 5, 2018 by user

5.2.1 Indices, PT3 Practice

Question 1:

(a) Simplify: a⁴÷ a⁷

(b) Evaluate:

${(2^{4})}^{\frac{1}{2}} \times 3^{\frac{1}{2}} \times 12^{\frac{1}{2}}$

Solution:

(a) a⁴÷ a⁷= a^4-7= a^-3

(b)

$\begin{array}{l} {(2^{4})}^{\frac{1}{2}} \times 3^{\frac{1}{2}} \times 12^{\frac{1}{2}} = 2^{2} \times 3^{\frac{1}{2}} \times {(4 \times 3)}^{\frac{1}{2}} \\ = 2^{2} \times 3^{\frac{1}{2}} \times {(2^{2} \times 3)}^{\frac{1}{2}} \\ = 2^{2} \times 3^{\frac{1}{2}} \times 2 \times 3^{\frac{1}{2}} \\ = 2^{3} \times 3 \\ = 24 \end{array}$

Question 2:

(a) Simplify: p³÷ p^-5

(b) Evaluate:

$10^{\frac{1}{2}} \times 5^{- \frac{1}{2}} \times {(2^{\frac{1}{2}})}^{5}$

Solution:

(a) p³÷ p^-5= p^3-(-5)= p³⁺⁵= p⁸

(b)

$\begin{array}{l} 10^{\frac{1}{2}} \times 5^{- \frac{1}{2}} \times {(2^{\frac{1}{2}})}^{5} \\ = {(2 \times 5)}^{\frac{1}{2}} \times 5^{- \frac{1}{2}} \times 2^{\frac{5}{2}} \\ = 2^{\frac{1}{2}} \times 5^{\frac{1}{2}} \times 5^{- \frac{1}{2}} \times 2^{\frac{5}{2}} \\ = 2^{\frac{1}{2} + \frac{5}{2}} \times 5^{\frac{1}{2} + (- \frac{1}{2})} \\ = 2^{3} + 5^{\frac{1}{2} - \frac{1}{2}} \\ = 2^{3} + 5^{0} \\ = 8 + 1 \\ = 9 \end{array}$

Question 3:

(a) Find the value of

$10^{\frac{4}{3}} \div 10^{\frac{1}{3}} .$

(b) Simplify (xy³)⁵ × x⁴.

Solution:

(a)

$\begin{array}{l} 10^{\frac{4}{3}} \div 10^{\frac{1}{3}} \\ = 10^{\frac{4}{3} - \frac{1}{3}} \\ = 10^{\frac{3}{3}} \\ = 10 \end{array}$

$\begin{array}{l} (b) {(x y^{3})}^{5} \times x^{4} = x^{5} y^{15} \times x^{4} \\ = x^{5 + 4} y^{15} \\ = x^{9} y^{15} \end{array}$

Question 4:

(a)

${(81 a^{8})}^{- \frac{1}{4}} =$

(b) Find the value of 2³× 2²

Solution:

(a)

${(81 a^{8})}^{- \frac{1}{4}} = \frac{1}{{(81 a^{8})}^{\frac{1}{4}}} = \frac{1}{{(3^{4})}^{\frac{1}{4}} {(a^{8})}^{\frac{1}{4}}} = \frac{1}{3 a^{2}}$

(b)

2³× 2²= 2³⁺²= 2⁵= 32

Question 5:

Find the value of the following.

(a)

$81^{\frac{3}{4}} \times 27^{- 1}$

(b)

$8^{\frac{2}{3}} \times 3^{- 2}$

Solution:

(a)

$\begin{array}{l} 81^{\frac{3}{4}} \times 27^{- 1} = {(\sqrt[4]{81})}^{3} \times {(3^{3})}^{- 1} \\ = {(3)}^{3} \times 3^{- 3} \\ = 3^{3 + (- 3)} \\ = 3^{0} = 1 \end{array}$

(b)

$\begin{array}{l} 8^{\frac{2}{3}} \times 3^{- 2} = {(\sqrt[3]{8})}^{2} \times \frac{1}{3^{2}} \\ = {(2)}^{2} \times \frac{1}{3^{2}} \\ = 4 \times \frac{1}{9} \\ = \frac{4}{9} \end{array}$

Question 6:

Find the value of the following.

(a)

$8^{\frac{4}{3}} \times {(3^{- 2})}^{3} \times 9^{\frac{3}{2}}$

(b)

$\frac{2^{- 2} \times 3^{2}}{2^{- 3} \times 81}$

Solution:

(a)

$\begin{array}{l} 8^{\frac{4}{3}} \times {(3^{- 2})}^{3} \times 9^{\frac{3}{2}} \\ = {(2^{3})}^{\frac{4}{3}} \times 3^{- 6} \times {(3^{2})}^{\frac{3}{2}} \\ = 2^{4} \times 3^{- 6} \times 3^{3} \\ = 16 \times 3^{- 6 + 3} \\ = 16 \times 3^{- 3} \\ = 16 \times \frac{1}{3^{3}} \\ = \frac{16}{27} \end{array}$

(b)

$\begin{array}{l} \frac{2^{- 2} \times 3^{2}}{2^{- 3} \times 81} = \frac{2^{- 2} \times 3^{2}}{2^{- 3} \times 3^{4}} \\ = 2^{- 2 - (- 3)} \times 3^{2 - 4} \\ = 2 \times 3^{- 2} \\ = \frac{2}{3^{2}} \\ = \frac{2}{9} \end{array}$

5.1 Indices

Posted on February 1, 2018 by user

5.1 Indices

5.1.1 Indices

1. A number expressed in the form aⁿ is known as an index notation.

2. aⁿ is read as ‘a to the power of n’ where a is the base and n is the index.

Example:

3. If a is a real number and n is a positive integer, then

4. The value of a real number in index notation can be found by repeated multiplication.

Example:

6⁴= 6 × 6 × 6 × 6

= 1296

5. A number can be expressed in index notation by dividing the number repeatedly by the base.

Example:

243 = 3 × 3 × 3 × 3 × 3

= 3⁵

5.1.2 Multiplication of Numbers in Index Notation

The multiplication of numbers or algebraic terms with the same base can be done by using the Law of Indices.

a^m× aⁿ= a^m^{+ n}

Example:

3³× 3⁸= 3³⁺⁸

= 3¹¹

5.1.3 Division of Numbers in Index Notation

1. The Law of indices for division is:

a^m÷ aⁿ= a^m^{- n}

Example:

4¹²÷ 4¹²= 4^12-12

= 4⁰

= 1

2. a⁰= 1

5.1.4 Raise Numbers and Algebraic Terms in Index Notation to a Power

To raise a number in index notation to a power, multiply the two indices while keeping the base unchanged.

(a^m)ⁿ= (aⁿ)^m= a^mⁿ

Example:

(4³)⁷ = 4³×⁷

= 4²¹

5.1.5 Negative Indices

$a^{- n} = \frac{1}{a^{n}}$

Example:

$5^{- 2} = \frac{1}{5^{2}} = \frac{1}{25}$

5.1.6 Fractional Indices

$a^{\frac{m}{n}} = \sqrt[n]{a^{m}} or {(\sqrt[n]{a})}^{m}$

Example:

$\begin{array}{l} 64^{\frac{2}{3}} = \sqrt[3]{64^{2}} or {(\sqrt[3]{64})}^{2} \\ = 16 \end{array}$